Sprinkler range revised

For an ideal fluid the velocity $v$ , the pressure $p$ and the elevation $y$ satisfies $\frac{1}{2}\rho v^2+\rho g y =p$ , where $\rho$ is the density and $g$ is the acceleration of gravity. We can turn this to $\frac {v^2}{2g}= y_0-y$ . Here $y_0=\frac{p_0}{\rho g}$ represents the pressure in the water line.

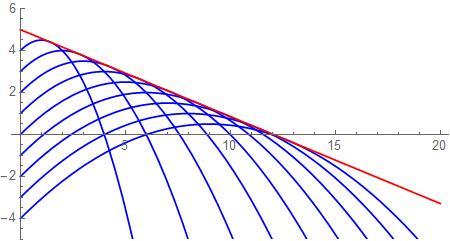
The range of the motion is (see, for example, here )

$d= \frac{v^2}{2g}\left[ 1 +\sqrt{1+\frac{2gy}{v^2 \sin^2 \theta}}\right]\sin 2 \theta = (y_0-y)\left[ 1 +\sqrt{1+\frac{2y}{y_0-y}}\right]$

for $\theta=45^{\circ}$ . The maximum of this function is at $y=-y_0/\sqrt{2}$ and at that point $d=y_0(1+\sqrt{2})$ . Interestingly, that is below ground level. At $y_0=0$ the range is smaller, $d=2 y_0$ . Any further increase of the elevation will reduce the range.

For smaller droplets, when the resistance by the air is relevant, the range will be smaller and it will depend on the size of the water droplets, creating a wide pattern of impact. This is actually an important factor in designing a good sprinkler. The calculation of the range requires numerical integration, see this web site .

See Laszlo Mihaly's explanation of this graph, including the fact that having the nozzle below ground gets the maximum range at ground level.