Sprinkler Zone

The relationship between $v$ and $r$ is $r = kv^2$ , where $k = \tfrac{\sqrt{3}}{2g}$ . Then the c.d.f of $r$ is $F_r(u) \; = \; P[r \le u] \; = \; P[v \le \sqrt{\tfrac{u}{k}}] \; = \; F_v\big(\sqrt{\tfrac{u}{k}}\big) \hspace{2cm} u > 0$ where $F_v$ is the c.d.f of $v$ . Thus the p.d.f of $r$ is $f_r(u) \; = \; F_r'(u) \; = \; \tfrac{1}{2\sqrt{ku}}f_v\big(\sqrt{\tfrac{u}{k}}\big) \; = \; \tfrac{1}{2\sqrt{ku}} \times \tfrac{1}{v_0^2} \sqrt{\tfrac{u}{k}} e^{-\frac{1}{v_0}\sqrt{\frac{u}{k}}} \; = \; \tfrac{1}{2kv_0^2}e^{-\frac{1}{v_0}\sqrt{\frac{u}{k}}}$ for $u > 0$ . Thus $f_r(u)$ is a decreasing function of $u$ , and so its maximum is achieved at $u=\boxed{0}$ .

I banged my head for awhile trying to figure out what this question was asking for, but here's what I eventually came to:

1) Suppose the landing distance is $R$ , and we divide the range of possible $R$ values into little bins of equal width $dR$
2) Each little bin of width $dR$ has an associated $dv$ , which I will show shortly
3) The probability of being in that particular bin of width $dR$ is equal to $f_v \, dv$
4) Find the $R$ value which maximizes the quantity from (3)

The relationship between $v$ and $R$ is:

$\large{R = \frac{2 v^2 \, sin \theta \, cos \theta}{g} \\ v^2 = \frac{g R}{2 \, sin \theta \, cos \theta }}$

We're interested in the relationships between the infinitesimals, so differentiate both sides with respect to $R$ :

$\large{2 v \, \frac{dv}{dR} = \frac{g}{2 \, sin \theta \, cos \theta} = \alpha \\ \frac{dv}{dR} \propto \frac{1}{v}}$

If we think of all the $R$ bins as having equal width, this comes to:

$\large{dv \propto \frac{1}{v} \\ f_v \, dv \propto \frac{1}{v} \, v \, e^{-v/v0} \\ f_v \, dv \propto \, e^{-v/v0}}$

The probability of being within a bin of width $dR$ is, somewhat counter-intuitively, maximized when the speed is zero, and the corresponding landing distance is zero. Or if you're uncomfortable with the 0/0 division that would imply when looking at some of the earlier math, you could pick some arbitrarily small value $\epsilon$

This problem highlights the subtleties of working with related probabilistic quantities. On first look things seem very counterintuitive: how can it possibly be that the most probable range for the projectile isn't the same thing as the range the projectile has when it's launched at its most probable speed? Given how much there is to grapple with, I wanted to fill in some of the context for the underlying manipulation of probability densities.

---

To get started, realize that the probability of any particular point in continuous distribution is zero. If we draw random reals from the range $\left(3, 4\right),$ there are an infinite number of possible numbers that can be drawn from the range, and each number is uniformly probable, so the probability of drawing any given real number is zero. Yet, we can confidently state that there is a $20\%$ chance of drawing a number that's between $3.3$ and $3.5.$

What this echoes is that we need to think about the probability of drawing a number from the neighborhood around a point, not the probability of a single point. Let's define $P(v_a, v_b)$ as the probability of drawing a number in the neighborhood between $v_a$ and $v_b.$ In terms of the probability density function $f_v(v),$ $P(v - \Delta v, v + \Delta v)$ is the integral $P(v - \Delta v, v + \Delta v) = \int\limits_{v - \Delta v}^{v + \Delta v}f_v(v)\, dv.$

Like @Steven Chase and @Mark Hennings point out, the range $r$ for a projectile is related to its launch speed $v$ and launch angle $\theta$ by $r(v) = 2v^2g^{-1}\cos\theta\sin\theta,$ which we can write more simply as $r = kv^2.$ This allows us to change between values of $v$ and values of $r.$ Because each outcome of $v$ corresponds to a physical outcome of $r,$ it must be true that the probability of observing a velocity in between $v_a$ to $v_b$ is equal to the probability of observing a range between $r(v_a)$ and $r(b_v).$

In other words:

$\begin{aligned} P_v(v_a, v_b) &= P_r(r(v_a), r(v_b)) \\ \int\limits_{v_a}^{v_b}f_v(v^\prime)\, dv^\prime &= \int\limits_{r(v_a)}^{r(v_b)}f_r(r^\prime)\, dr^\prime \end{aligned}$

We can use this equality to find the probability density of $r,$ $f_r(r),$ in terms of the probability density of $v,$ $f_v(v).$ For simplicity, we can set $v_a = 0$ (which implies $r(v_a) = 0,$ and let $v_b = v$ vary so that we can just think about $P(0, v) = P_v(v),$ the probability of observing a velocity between $0$ and $v.$

From above, we have

$\begin{aligned} P_v(v) &= P_r(r(v)) \\ \int\limits_0^{v}f_v(v^\prime)\, dv^\prime &= \int\limits_0^{r(v)}f_r(r^\prime)\, dr^\prime. \end{aligned}$

How can we generate a relationship between the integrands? We can take the derivative of both sides with respect to one of the integration variables and use the chain rule to connect them.

Taking the derivative of both sides with respect to $v,$ we have $\begin{aligned} f_r(r) &= \frac{d}{dr} \int\limits_0^v f_v(v^\prime)\, dv^\prime \\ &= \frac{dv}{dr}\cdot \frac{d}{dv}\left[\int\limits_0^v f_v(v^\prime)\, dv^\prime\right] \\ &= \frac{dv}{dr}f_v(v) \end{aligned}$

Using the relationship between $r$ and $v,$ we can see that $\frac{dv}{dr} = \sqrt{\frac{1}{k}}\frac{d}{dr}\sqrt{r} = \frac{1}{2}\sqrt{\frac{1}{kr}}.$

which gives us $f_r(r) = \frac{1}{2}\sqrt{\dfrac{1}{kr}} f_v(v) = \frac{1}{2}\sqrt{\dfrac{1}{kr}} \frac{v}{v_0^2}e^{-v/v_0}.$ Upon replacing $v$ with $v(r),$ we find

$\begin{aligned} f_r(r) &= \dfrac{1}{2}\sqrt{\dfrac{1}{kr}}\sqrt{\dfrac{r}{k}}\dfrac{1}{v_0^2}e^{-\sqrt{r/k}/v_0}\\ &= \boxed{\dfrac{1}{2kv_0^2}e^{-\sqrt{r/kv_0^2}}} \end{aligned}$

Obviously, $f_r$ is maximized when $r$ is $0,$ and this means that the probability of ranges is highest in the neighborhood of $r=0.$ We can check to see that this is true by randomly sampling $v$ from the probability density $f_v(v),$ transforming them according to $r = kv^2,$ and making a histogram of the corresponding values of $r.$

Here is a random sample of 20,000 speeds drawn from the distribution $f_v(v),$

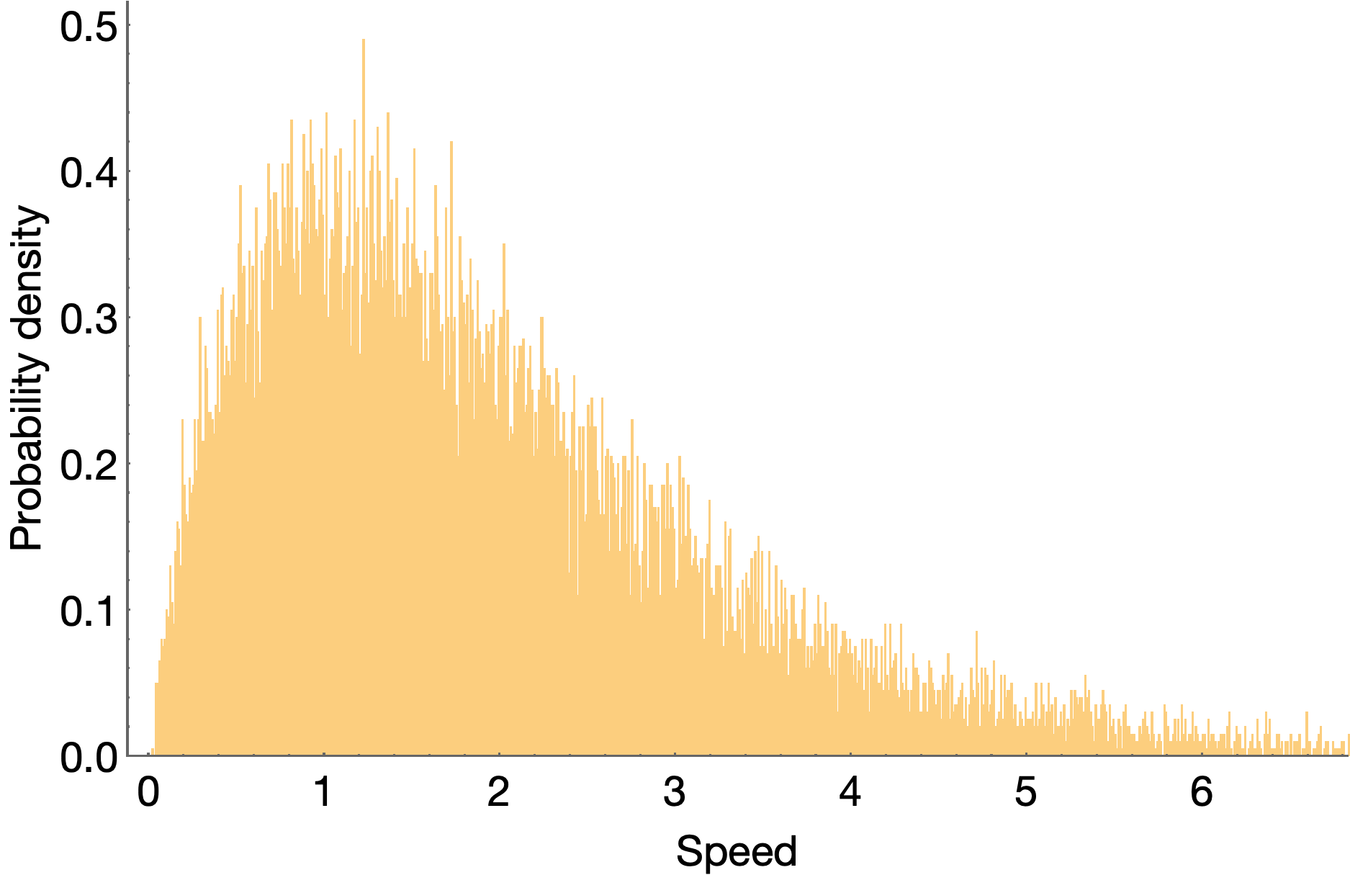
and here is the distribution of ranges, which is obtained by simply transforming each value in the histogram above according to $r = \left(2g^{-1}\sin\theta\cos\theta\right)v^2:$

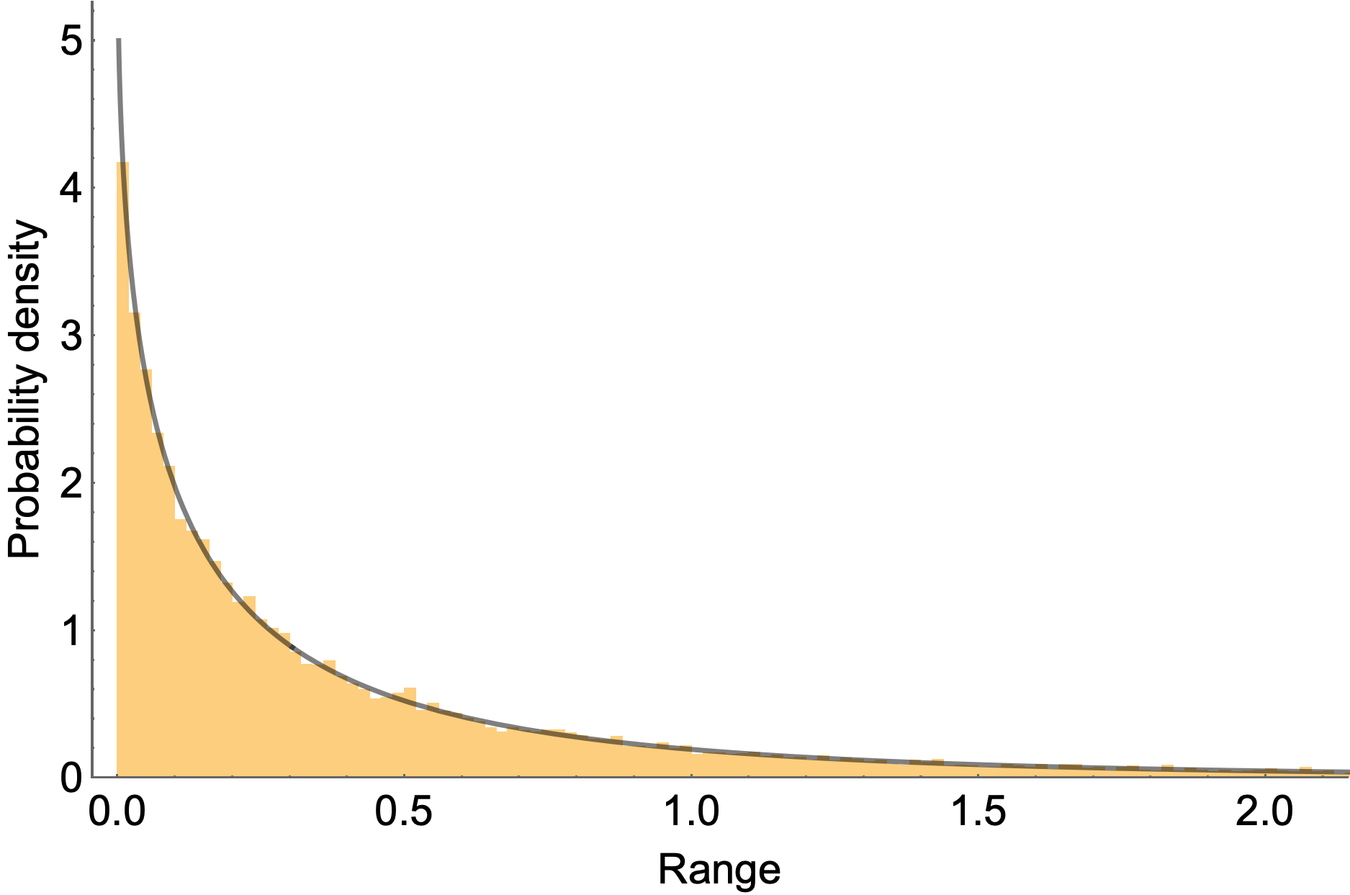
The yellow bars show the frequency density of the sampled ranges, and the black curve shows the prediction according to our result above.

Transforming the distribution from velocity (v) to range (R) using

F(R)dR = f(v)dv,

where R=(v^2)sin(60°)/g,

gives, F(R)=A.exp(-√R/B), with A and B constants.

which gives R=0 as most likely value, as the function F(R) is maximum at R=0,

Answer, R=0