Spyrals!
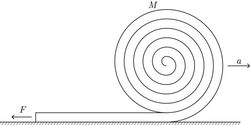 A hose of mass
and length
is made into a coiled roll of radius
. The hose is then unrolled across a level ground with initial speed
, while the free end is held at a fixed point on the ground. The hose unrolls and becomes straight.
A hose of mass
and length
is made into a coiled roll of radius
. The hose is then unrolled across a level ground with initial speed
, while the free end is held at a fixed point on the ground. The hose unrolls and becomes straight.
Determine the time taken by the hose to completely unroll.
Details and Assumptions
-
.
-
At all instant, the hose is performing pure rolling.
-
The hose is arbitrarily flexible.
-
The work necessary for its deformation, air resistance and rolling resistance can be neglected.
-
.
The answer is 9.523.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can represent mass as a funtion of distance covered x , m ( x ) = M ( 1 − L x )
Now, since R ≪ L , we can neglect Upward velocity and Potential Energy,
2 1 M v 0 2 + 2 1 M R 2 ( R v 0 ) 2 ⇒ v 2 ( x ) ⇒ v ( x ) ⇒ v 0 1 0 ∫ L 1 − L x d x ⇒ T = 2 1 m ( x ) v 2 ( x ) + 2 1 m ( x ) r 2 ( r v ( x ) ) 2 = m ( x ) m v 0 2 = 1 − L x v 0 = ∫ d t = T = v 0 L 0 ∫ 1 1 − u d u = 3 v 0 2 L
∴ T = 3 v 0 2 L ≈ 9 . 5 2 3 8 0 9