How many 17s?
1 7 2 + 1 7 2 + 1 7 2 + . . . + 1 7 2 + 1 7 2 + 1 7 2 = 1 7 2 + 1 7 2 + 1 7 2
How many times should 1 7 2 appear under the square root sign for the equation above to be true?
The answer is 2601.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
27 solutions
superb....!
How can the answer be 2061 when it is asking for the number of times!!!!!!!!!!!!!
Log in to reply
2601 no. of times 17^2 would be under the root.
I agree, sqrt a square and they cancel each other out. This solution suggests 2601 * 17 which does not equal 17^2 * 3... The answer should be 51!
what a fantastic explanation man!
wow,,,get outta here man
In response to niranjan khanderia....... The answer should be 867 becoz 3 17^2= 867......and (9 17^2 17^2)^1/2 when you take 9 out, how it can be still 9? It should be 3 when it comes out. So 3 17^2= 867 LHS=RHS
3*17^2=867 wtf get your math together.
beautiful <3
N17'2 = 17'2 + 17'2+ 17'2 there fore 17n =17'2+17'2+17'2 n = 17 + 17 +17 N = 51'2 = (2601)
We can write the equation as follows:
Because appears times under the square root sign, we can write:
Squaring both sides:
Dividing by :
Log in to reply
N17'2 = 17'2 + 17'2+ 17'2 there fore 17n =17'2+17'2+17'2 n = 17 + 17 +17 N = 51'2 = (2601)
We can write the equation as follows:
Because appears times under the square root sign, we can write:
Squaring both sides:
Dividing by :
did the same way
amazingly solve this problem.
i wasn't expecting that O_O
Beautiful explanation. Just great.
3×17×17 is not equal to 9×17×17
Log in to reply
3 = 9 , so when this three goes inside the square root sign it becomes 9.
We can write the equation as follows:
1 7 2 + 1 7 2 + 1 7 2 + . . . + 1 7 2 + 1 7 2 + 1 7 2 = 1 7 2 + 1 7 2 + 1 7 2
1 7 2 + 1 7 2 + 1 7 2 + . . . + 1 7 2 + 1 7 2 + 1 7 2 = 1 7 ( 1 7 ⋅ 3 )
Because 1 7 2 appears n times under the square root sign, we can write:
n ⋅ 1 7 2 = 1 7 ( 1 7 ⋅ 3 )
Squaring both sides:
n ⋅ 1 7 2 = 1 7 2 ( 1 7 2 ⋅ 9 )
Dividing by 1 7 2 :
n = ( 1 7 2 ⋅ 9 )
n = ( 2 8 9 ⋅ 9 )
n = 2 6 0 1
My immediate answer was 9 LOL. I thought that the 17's were not relevant.
Log in to reply
Same here :p
Me too... Hahahahaha
Calvin Lin (staff) please check whether the answers are relevant as I came to this page for an entirely different sum. My email for further info: akhashrajaraam @gmail.com
Is it coincidence that I did the same?
is that someone answer 51....
Log in to reply
I answered 51 also lol
I answered 51, because 51(17^2) under square root = 867 wich is = (17^2 +17^2 +17^2), I don't know my mistake
Log in to reply
@Luis Pedro – I did the same thing. because all those (17^2) under a square root cancel to be just 17. 3(17^2)= 867 867/17=51. That's correct maths for sure.
Log in to reply
@Ryan Hancock – @Ryan Hancock you have to consider that the sqrt(17²×n) ≠ 17n, but to 17sqrt(n) so that all those 17² don't just cancel to be just 17 each, but the number of 17s also reduces to the square root of the original number of 17²s under the sqrt, so that sqrt(51×17²) = 17 × sqrt(51) = 17 × sqrt(17)× sqrt(3) that's why there aren't just 51 17²s under the sqrt, but 51² (2601) of them such that under the same procedure sqrt(51²×17²) = 51×17 = 3×17×17 = 3×17². I hope it's clear why the answer is 2601
@Luis Pedro – 1 7 2 ⋅ 5 1 < 1 7 ⋅ 8 = 1 3 6 < 8 6 7 = 1 7 2 ⋅ 3
i too answered as 9
Victor, very good problem and fun. Thank you for problem.
Great great !how didn't think au bout this !
The question is not what is the number under the square root sign, but but how many times is the number 17 squared to appear under the square root sign. The number is two, which, when multiplied by nine give the result.
We can write the equation as
n 1 7 2 = 1 7 2 + 1 7 2 + 1 7 2
therefore
1 7 n = 1 7 2 + 1 7 2 + 1 7 2 n = 1 7 + 1 7 + 1 7
n = 5 1 2 = 2 6 0 1
Same solution I used, and definitely the easiest.
Easy solution and I have also solved the problem in this method.
Easiest method to arrive at the answer
n × 1 7 2 = 3 × 1 7 2
n × 1 7 2 = 9 × 1 7 4
n = 9 × 1 7 2 = 2 6 0 1
The cleanest.
Wrong solution mate
Rewriting the equation as x = 3 ( 1 7 2 )
Squaring both sides gives us x = ( 3 ( 1 7 2 ) ) 2 = 1 7 2 ( 1 7 2 ( 9 ) ) So 9 ( 1 7 2 ) = 2 6 0 1
Let S = 1 7 2 + 1 7 2 + . . . + 1 7 2 = k × 1 7 2 . We know that S = 1 7 2 + 1 7 2 + 1 7 2 = 3 × 1 7 2 . From this, we get S 2 = k × 1 7 2 = ( 3 × 1 7 2 ) 2 = 9 × 1 7 4 . Let's find k : k = 1 7 2 9 × 1 7 4 = 2 6 0 1 . So 17^2 needs to be 2601 times under the sqare root to let S equals 3 × 1 7 2 .
Thanks for sharing your approach, Romain. The solution is well-presented and is easy to understand.
If we let x equal 17,
x = 1 7
we can write the equation like x 2 + x 2 + x 2 = 3 ⋅ x 2 = x 2 + x 2 + x 2 + … + x 2 = n ⋅ x 2 Or just
3 ⋅ x 2 = n ⋅ x 2
We can now square both sides 9 ⋅ x 4 = n ⋅ x 2
and isolate n
n = x 2 9 ⋅ x 4 = 9 ⋅ x 2
Now we replace our x with 17 n = 9 ⋅ 1 7 2 = 9 ⋅ 2 8 9 = 2 6 0 1
( 1 7 2 ∗ 3 ) 2 = 751689
2 8 9 7 5 1 6 8 9 = 2601
This is equal with √(16+16+16+⋯+16+16+16)=16+16+16. There fore to get 48 or 16+16+16 we should have 48*48 in the radical sign. That is 2304. This implies we should have {(2304)/(16)}th 16 in the radical sign. that is 144 16s should have.
n 1 7 2 = 9 × 1 7 4 n = 9 × 1 7 2 = 2 6 0 1
squaring both sides gives 1 7 2 + 1 7 2 +...+ 1 7 2 = 3 2 × 1 7 4 = (9 × 1 7 2 ) × 1 7 2 . The term in the brackets tells us how many 1 7 2 are required. Let this value be n .
∴ n = 9 × 1 7 2 = 2 6 0 1
Note that: 3 × 1 7 2 = 8 6 7
Then 8 6 7 2 = 7 5 1 6 8 9 giving us the result: 7 5 1 6 8 9 / 1 7 2 = 2 6 0 1
|17^2=x| sqrt(x+x+x+x+x....)=sqrt(ax)| a = number of times x is added| sqrt(ax)=3x| ax=9x^2| a=9x| a=(9)17^2| a=(9)289| a=2601| 17^2 should appear 2601 times under the sqrt.|
We need something who’s square root is 1 7 2 + 1 7 2 + 1 7 2 so let’s look at ( 3 × 1 7 2 ) 2 or 3 2 × 1 7 4 , and 1 7 4 = ( 1 7 2 ) 2 = 1 7 2 × 1 7 2 so we need 1 7 2 lots of 1 7 2 added together to make a single 1 7 4 and we need 3 2 × 1 7 4 to be rooted. Or 3 2 × 1 7 2 × 1 7 2 so there needs to be 3 2 × 1 7 2 = 2 6 0 1 1 7 2 s added together.
simple solution, we can interpret as:
x 1 7 2 = 8 6 7
1 7 x = 8 6 7
x = 1 7 8 6 7
x = 5 1
x = 2 6 0 1
RHS we have 17^{2}+17^{2}+17^{2}=867 Further it is equal to \sqrt{867×867} On factorising we get- \sqrt{17^{2}×3×867} \sqrt{17^{2}×2601}
Hence,17^{2} should have to appear \boxed{2601} times ... Q.E.D.
Let X = 1 7 2 . The equation in the question can be rewritten as follows:
n X = 3 X
where n is the number of X's required under the square root. Solving for n :
n = 9 X = 9 × 1 7 2 = 2 6 0 1
as required.
We can rewrite 1 7 2 + . . . + 1 7 2 = 1 7 2 + 1 7 2 + 1 7 2 as a ∗ 1 7 2 = 3 ∗ 1 7 2 . By squaring both sides of the equation, we obtain a ∗ 1 7 2 = 9 ∗ 1 7 4 = a ∗ 1 7 2 ∗ 1 7 2 → a = 1 7 2 ∗ 9 = 2 6 0 1
We can write the equation as √n.17^2=3.17^2 √k.17^2=3.17^2;where n=k.17^2 K=9 n=9×17^2=2601
Rewrite all the 17s as a 1 7 2 and equate this to 3 ( 1 7 2 ) Square both sides... a . 1 7 2 = ( 3 . 1 7 2 ) 2 = 9 . 1 7 2 The number of 17s required is a which is a = 9 . 1 7 2 = 2 6 0 1
we can solve this in this way --- ( 3 * 17^2)^2=(9 * 17^2 * 17^2)=2601 * 17^2 , as we need to keep 3...... squared 17.
Let x be number of times 17^2 will appear
therefore, (x.17^2)^1/2 = 3.17^2
squaring both sides,
x.17^2 = 9.17^2.17^2
x.17^2 = 2601.17^2
x = 2601
We can derive algebraic formula for this. By deriving the formula i.e. 9×a^2 and putting a=17 we get 9×17^2 =9*289=2601
We need LHS to be 9 17^4 and that can happen if there are 9 17^2 = 2601 terms inside the square root.
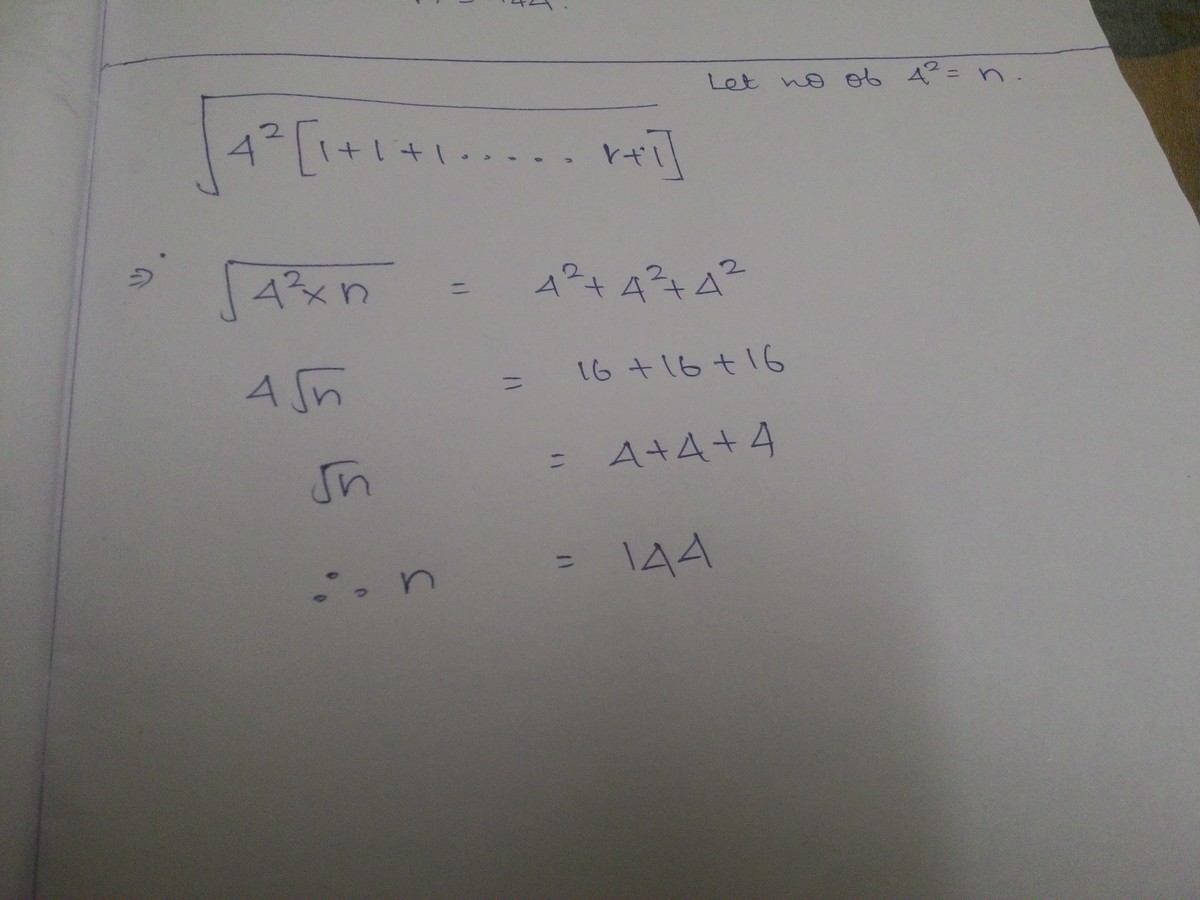
1 7 2 + 1 7 2 + 1 7 2 = 3 ∗ 1 7 2 = 9 ∗ 1 7 2 ∗ 1 7 2 = 9 ∗ 1 7 2 ∗ 1 7 2 . 9 ∗ 1 7 2 = 2 6 0 1