This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice solution
Great solution.
nice sol.....
Great solution.
Is there any generealised method of solving these kind of problems?
Log in to reply
No general formula for any random/ irregular figure. However, there are some general formulas as follows:-
If there is a n x n square [an array of (n+1)x(n+1) points], then :-
(a) no. of squares within this square = ∑ n 2
(b) no .of rectangles within this square = ∑ n 3 = ∑ n . ∑ n
If there is a m x n rectangle [an array of (m+1)x(n+1) points], then :-
(c) no. of squares within this rectangle = m n + ( m − 1 ) ( n − 1 ) + ... until ( m − x ) or ( n − x ) become 1
(d) no .of rectangles within this rectangle = i = 1 ∑ m i j = 1 ∑ n j
Maybe you should Call your squares more speciffic a linear square or something Else. Cause you Can easily Think that it was random squares. ;-)
I did not even attempt to answer this question because there wasn't even any algebraic information on the side lengths of the rectilineal figures.
Log in to reply
Are you trying to say that you needed those squares to be confirmed as squares before you would class them as such? Just look at them! Clearly approximate, if not exact, squares - compared to very clear rectangles.
Log in to reply
In mathematics, you cannot take anything for granted (and I also forgot to mention about the angles - there is no information on their measures).
Log in to reply
@Sobhan Bihan – With the information you're given, if there is no answer of 'more information needed', I think you can safely assume that each of the approximate squares above ARE exact.
1 * 1 square = 5
2 * 2 square = 5
3 * 3 square = 1
So, Total 11.
11 squares .
Start by counting the biggest squares which is 1 .. Then count the smaller ones which are 5 .. Then the smallest ones which are 5 .. So the total number is 10 squares .
Just to make this more clear, the inventory is like this:
-
3x3: 1 square
-
2x2: 5 squares
-
1x1: 5 squares
I didn't know 1 + 5 + 5 added to 10 !! :)
In response to Sobhan Bihan: What u say is absolutely true but SOMETIMES, we need to rely more on our visual senses.... Also, isn't there any other way in which we can solve this question instead of counting??? It wud b of great help...
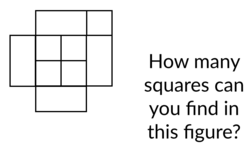
11 squares! We have five squares that measure 1x1, five squares that measure 2x2, and one square that measures 3x3.