Square In A Haystack
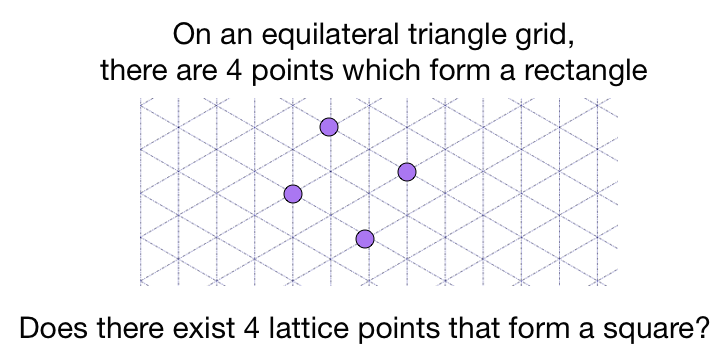
The above shows a part of an infinitely large equilateral triangular grid. The four purple lattice points form a rectangle.
Is it possible to form a square by connecting some four lattice points on the grid?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Sir, how did you get √2 ?
Log in to reply
If X Y Z W is a square with X Y ⊥ Y Z , what is the ratio of ∣ X Y ∣ ∣ X Z ∣ ? This is the ratio of the diagonal to the side of the square.
For any two lattice points on this grid, a third point which forms equilateral triangle with these two points is also a lattice point. (The proof of this should be easy so I am not showing it)
Now suppose there are squares of lattice points on this plane.
Pick the smallest one.
However, we can construct a smaller one base on this square:
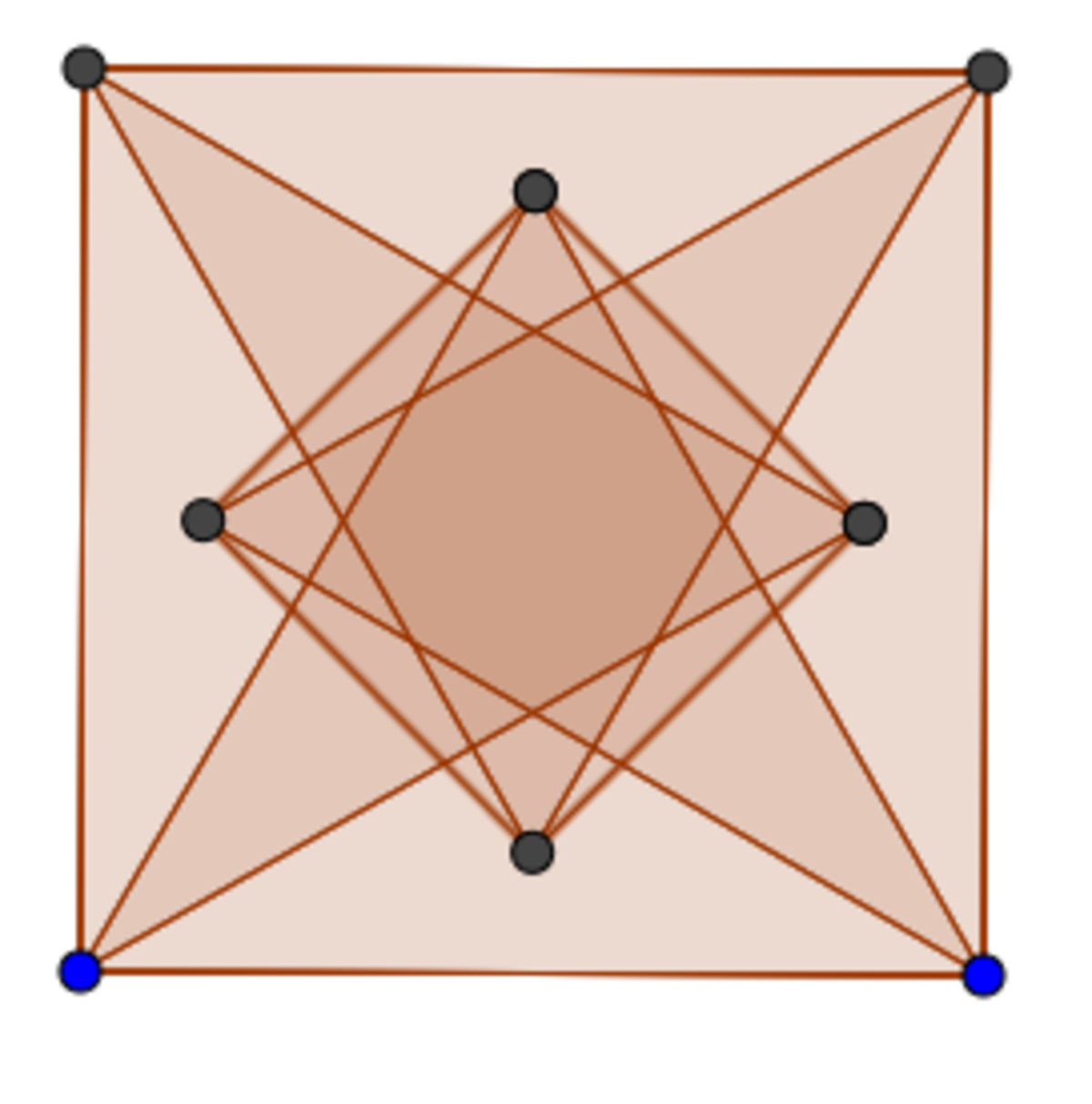
which leads to a contradiction to the 'smallest' assumption.
So there does not exist squares of lattice points on this plane.
Very nice infinite descent argument!
As a side note, you should explain why there exists a "smallest square". For example, if there were squares of side length n n + 1 , then there is no "smallest square" in this sequence.
Log in to reply
Thank you! Actually I am not familiar with this part so I skipped it and pretend that nobody will notice...
Anyway, I will try to prove it:
Define two unit vectors
i
^
,
j
^
which are
6
0
∘
apart (instead of
9
0
∘
in usual).
Position of lattice points on the plane can be denoted as
x
i
^
+
y
j
^
where
x
,
y
∈
Z
when one of the lattice point is picked as origin and the plane is oriented appropriately.
Let
A
=
a
i
^
+
b
j
^
,
B
=
c
i
^
+
d
j
^
(
a
,
b
,
c
,
d
∈
Z
) be two lattice points on the plane.
∣
A
B
∣
2
=
A
B
⋅
A
B
=
(
(
c
−
a
)
i
^
+
(
d
−
b
)
j
^
)
⋅
(
(
c
−
a
)
i
^
+
(
d
−
b
)
j
^
)
=
(
c
−
a
)
2
+
(
d
−
b
)
2
+
2
(
c
−
a
)
(
d
−
b
)
i
^
⋅
j
^
=
(
c
−
a
)
2
+
(
d
−
b
)
2
+
2
(
c
−
a
)
(
d
−
b
)
cos
6
0
∘
=
(
c
−
a
)
2
+
(
d
−
b
)
2
+
(
c
−
a
)
(
d
−
b
)
angle between
i
^
and
j
^
is
6
0
∘
which is an integer.
Integer is well-ordered, and squaring preserves ordering.
Therefore, the length of sides are also well-ordered.
Thus we can find a smallest square.
Log in to reply
Great! That's one way of doing it.
Another possibility is to calculate the ratio of the lengths of the squares that we generated as r < 1 , which is a fixed ratio regardless of the original square's side length. From which, it follows from the existence assumption, there is a square of side length r n L for all n , which eventually gets too small. Hence, contradiction.
This works because we have constant scaling, as opposed to the { n n + 1 } example that I gave above.
Log in to reply
@Calvin Lin – Yours approach is much more concise than mine! Thanks for teaching me this approach. =D
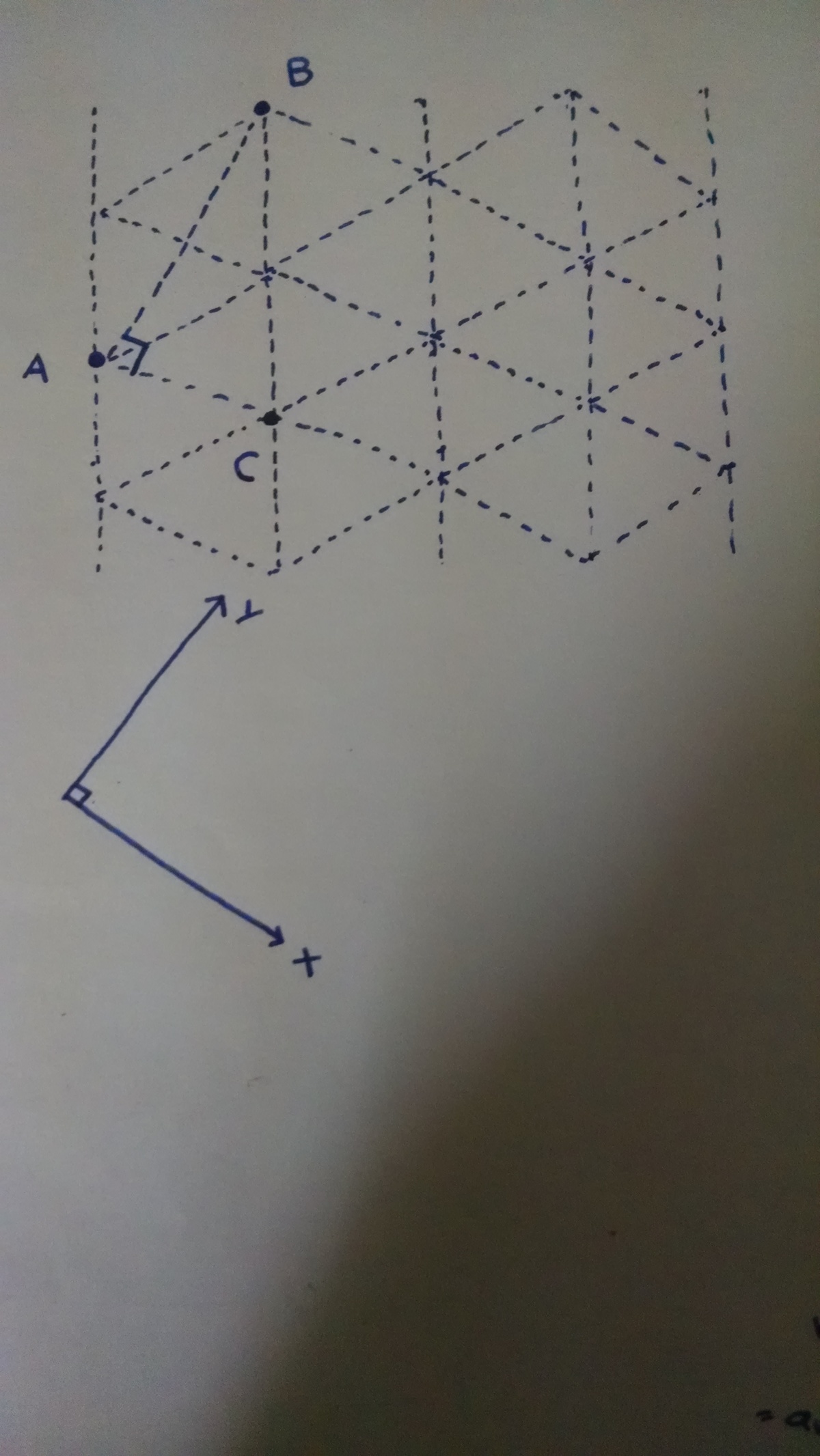 Let the sides of the equilateral triangle be
a
.
Let the sides of the equilateral triangle be
a
.
Now Consider 2 axes mutually perpendicular to each other because the angle contained by the sides of a square is 90°
Let one axis be along the sides of the triangles(X axis), while the other be along the height of the equilateral triangles(Y axis)
To go from one lattice point to other on the X axis, we must go in multiples of a
Therefore, one side of the square is n . a for integral n .
Similarly, to move from one lattice point to the other on the Y axis, we must go in multiples of 3 a
Therefore, another side of the square is m . 3 a for integral m .
But the sides of a square are equal, which implies m . 3 . a = n . a
Therefore m n = 3 .
But n and m are integral and thus LHS is rational, however RHS is irrational.
Hence, it is impossible to embed a square on this lattice.
P.S. : For those wondering why to take two integers m and n , consider a rectangle with dimensions 2x3 You totally need 6 rectangles to form a square(6x6).
Good analysis! Why must we have "let one axis be along the sides of the triangle"?
Why isn't it possible to have a square where no edge is along a lattice gridline?
E.g. In the rectangular grid that we're used to, ( 1 , 0 ) , ( 2 , 1 ) , ( 1 , 3 ) , ( 0 , 1 ) form a square where no edge is along a gridline.
To attach a picture, click "Edit" (your solution), then click this button

Log in to reply
I am using the app, which I think currently doesn't support an attachment. Maybe I'll post the picture tomorrow from PC. Thanks anyways. :)
Let l be the side of the triangle. We know that its area is A = 4 l 2 3 . For any two points we choose, we can determine the square's side. Letting n be the amount of triangles between the two chosen points, n l will be the square's side, with n ∈ Z . If it were possible to form a square choosing any four points among the vertices, we would have that m A = n 2 l 2 , where n 2 l 2 is the area of the square and m represents the amount of triangles inside the square and has to be, necessarily, an integer.
m 4 l 2 3 = n 2 l 2
m = 3 n 2 4 3
We can clearly see that m isn't an integer and, therefore, a whole number of triangles can't fill the square.
Why must there be an integer number of triangles between any two chosen points?
IE What is the n corresponding to these 2 points?
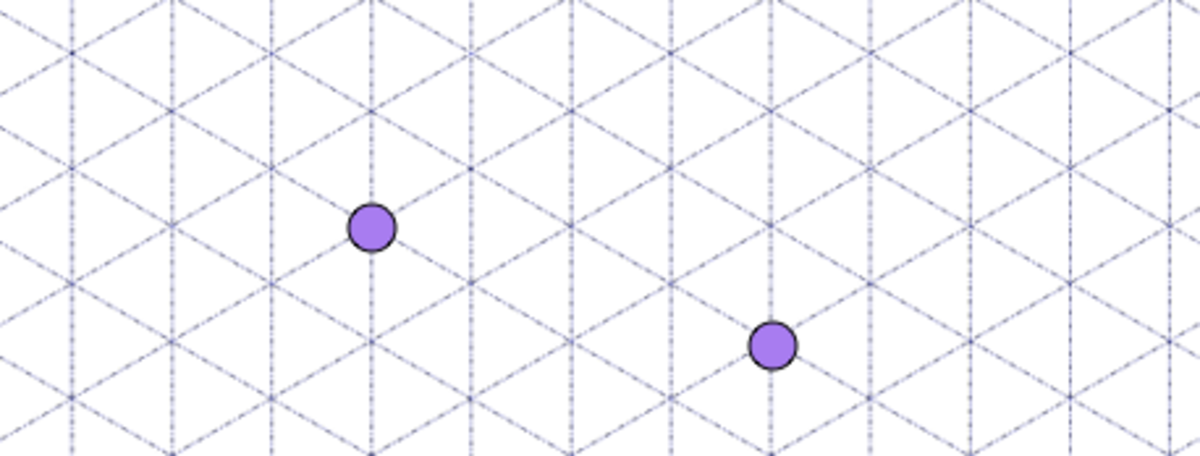
Log in to reply
Good point, n wouldn't be an integer in that case and in many other cases. My attempt at the problem was too simplistic, I'll keep trying.
Log in to reply
You are not too far off from the actual proof. Find a way to express these points in the lattice grid, in order to calcualte the lengths and angles.
It is not possible to form any square by taking any four points, it will lead to the formation of quadrilateral whose two adjacant angle will be (
6
0
°
and
1
2
0
°
) or
9
0
°
, and the resulting quadrilateral formed will be either
(
r
h
o
m
b
u
s
or
p
a
r
a
l
l
e
l
o
g
r
a
m
or
t
r
a
p
e
z
i
u
m
) or
r
e
c
t
a
n
g
l
e
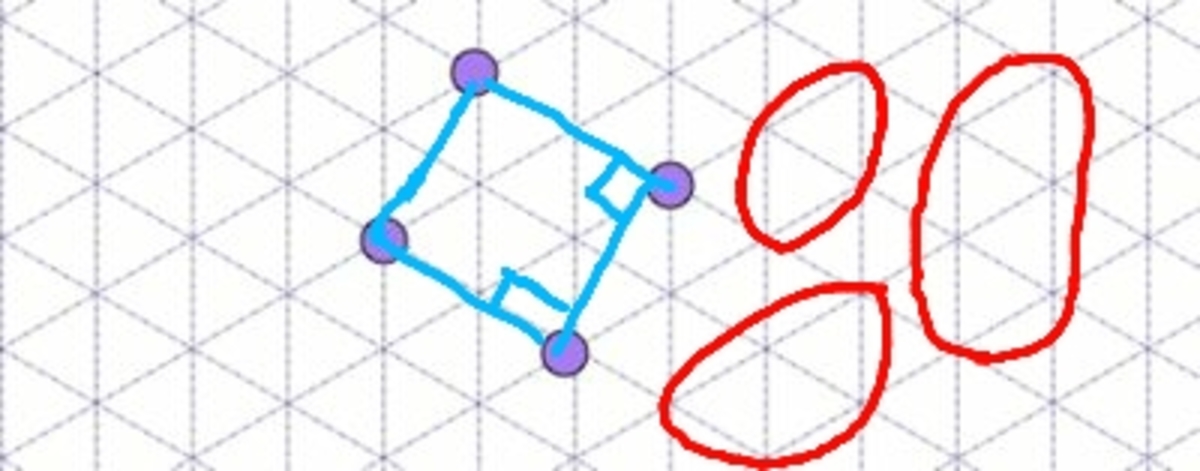
for further clarification you may ask any questions
Moderator note:
This solution is merely an assertion. It doesn't constitute a proof that we cannot obtain a square. In particular, since squares are also rectangles, it is not clear why we cannot get a square.
Got a proof?
Why must the 4 points be "close" together? They could be any 4 points on the entire lattice grid.
It's not too hard to find 3 points that give a right angle. For example, these 4 points give us a rectangle:
 .
.
Note also that since squares are rhombuses, you have not ruled out being able to find a square.
Log in to reply
You have connected 4 points that forma right angle, but still it is not a square (all sides are not of same length)
Log in to reply
I did not say it is a square. I said:
For example, these 4 points give us a rectangle.
The point is that your statement of "it will lead to the formation of quadrilateral whose two adjacent angles will be 6 0 ° and 1 2 0 ° " is not true, because you are only considering "consecutive points in a line", instead of any 2 arbitraty points on the grid. (IE You only considered points that were "close together" and thought that we could only get those 2 angles)
The lattice points of this triangular grid can be represented by integer pairs ( a , b ) , where the distance between ( a , b ) and ( c , d ) by cosine rule is
( a − c ) 2 + ( b − d ) 2 − 2 ( a − c ) ( b − d ) cos 6 0 ∘ = ( a − c ) 2 + ( b − d ) 2 − ( a − c ) ( b − d ) .
To show that we cannot find 4 points which form a square, we will show that there does not exist 3 distinct points X = ( a , b ) , Y = ( c , d ) , Z = ( e , f ) such that ∣ X Y ∣ = ∣ Y Z ∣ and X Y ⊥ Y Z .