Square on a Hexagon
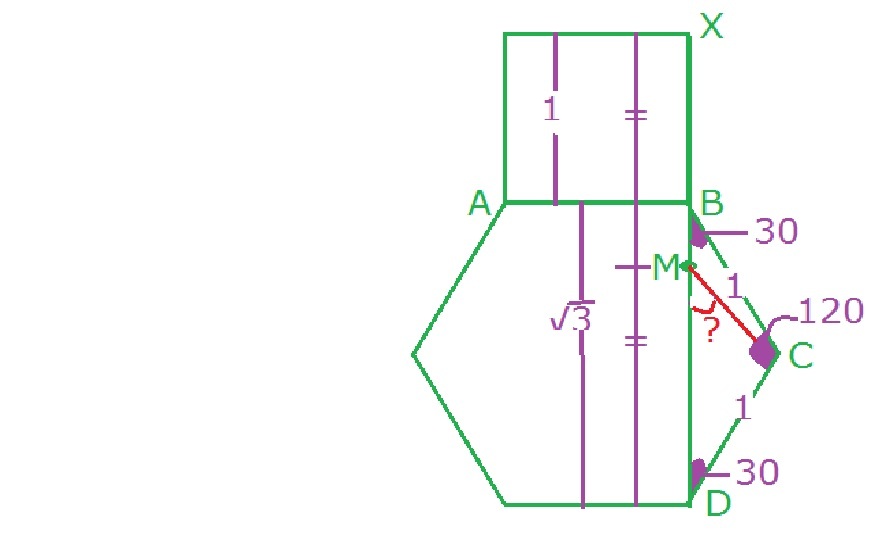
A B C D E F is a regular hexagon. Square A B X Y is constructed on the outside of the hexagon. Let M be the midpoint of D X . What is the measure (in degrees) of ∠ C M D ?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Sorry, that should be D M = 2 D B + B X , not D M = 2 D B + D X
Log in to reply
I wouldn't have even noticed the typo if you hadn't pointed that out!
A very well written solution! I'm voting you up!
Log in to reply
Oh, but I make typos lately in writing solution. Anyway, thank you.
Amazing solution. Well done dude!
Without loss of generality, let the side length of the hexagon be 2 , and let the foot of the perpendicular from C to D X be P . Then △ B C P and △ P C D are congruent 3 0 − 6 0 − 9 0 right triangles, so B P = P D = 3 . We know that B X = 2 , so D X = 2 + 2 3 .
Since M is the midpoint of D X , we have D M = 1 + 3 . Since P D = 3 , we have P M = 1 . Then △ P M C is an isosceles right triangle. Therefore, m ∠ C M D = m ∠ P M C = 4 5 ∘ .
I really like your solution as well! Could you tell me if there is anything restraining me to assume certain points without loss of generality when it comes to these kinds of more... "general" problems? Is there anything I should look out for before I use this method?
Log in to reply
WLOG is justified in this case, because we can scale the diagram to achieve any side length for the regular hexagon.
Log in to reply
Yes, I am aware why it is possible here, but how can I tell (other that using my instinct or just simply checking) if WLOG can be used within a problem or not? Or is it just plainly obvious most of the time?
Log in to reply
@Ivan Sekovanić – When there is a problem in which something isn't specified and the problem asks for something not related to that thing, you can usually do WLOG. For example, if you're not given the side lengths of anything and you want to find the ratio between two areas, you can usually assume.
Log in to reply
@Michael Tang – Aha, interesting. That's exactly the answer to my question. Thank you very much!
Log in to reply
@Ivan Sekovanić – I think when the required answer is a ratio or an angle we can use WLOG. If the value of the thing we have used in WLOG, is given we can not use WLOG. If the value is given, often it is reductant and the author has done so knowingly (to confuse the reader or make the problem simple.) or unknowingly (the author lake of understanding.)
We let the side of the hexagon be 1 . We drop the perpendicular from C to BD, and let the projection from C to BD be K. Since BC=CD, ∠ C B D = ∠ C D B , so ∠ B C K = ∠ D C K = 2 1 2 0 ∘ = 6 0 ∘ . Thus B K = s i n ( 6 0 ∘ ) B C = 2 3 ( 1 ) = 2 3 . Also, C K = c o s ( 6 0 ∘ ) B C = 2 1 ( 1 ) = 2 1 . Similarly D K = 2 3 , so X D = 1 + 2 2 3 = 1 + 3 . Hence D M = 2 1 + 3 , so K M = 2 3 + 1 − 2 3 = 2 1 = C K . Thus ∠ C M K = ∠ C M D = ∠ M C K . Since ∠ C M K + ∠ K C M = 1 8 0 ∘ − ∠ C K M = 1 8 0 ∘ − 9 0 ∘ = 9 0 ∘ , ∠ C M K = ∠ C M D = 2 9 0 ∘ = 4 5 ∘ .
Let the midpoint of B D be N . Let C N = x .
Since A B C D E F is a hexagon, △ D C N and △ B C N are 30-60-90. Therefore, B C = 2 x and B N = N D = x 3 . Since A B C D E F and A B X Y have the same side length, B X = 2 x . Therefore, D X = 2 x 3 + 2 x , and so D M = x 3 + x . We subtract length D N = x 3 to get M N = x . Therefore, since m ∠ M N C = 9 0 ∘ and M N = x = N C , the answer is m ∠ C M D = 4 5 ∘ .
Without loss of generality, we may conveniently assume length of each side as 2.
Let O be the centre of the regular hexagon.
AD passes through O, is of length 4 and by Pythagoras DE^2 = 16 - 4 = 12 .
So DX = \sqrt{12}. + 2 = 2(\sqrt{3}. + 1).
Let M be the midpoint of DX, So DM =\sqrt{3}. + 1.
Let N be the foot of the perpendicular from C upon DE.
Clearly DN = NE = \sqrt{3}.
and CN = \sqrt{4 -3}\ = 1.
Thus MN = DM - DN = 1 = CN .
Hence CNM is a right angled isosceles triangle and angle CMN (or CMD) = 45 degrees.
W L O G l e t A B = 1 . W e k n o w Δ B C D i s 1 − 1 2 0 o − 1 . ∴ B D = 3 a n d ∠ s C B D = B D C = 3 0 . ∠ s A B D = A B C − C B D = 1 2 0 − 3 0 = 9 0 . ⟹ X B D i s a s t . l i n e . ∴ X D = X B + B D = 1 + 3 , ⟹ M D = 2 1 ( 1 + 3 ) . I n Δ M D C : − U s i n g C o s R u l e t o f i n d l e n g t h o f M C . M C 2 = M D 2 + D C 2 − 2 ∗ M D ∗ D C ∗ C o s B D C = ( 2 1 ( 1 + 3 ) ) 2 + 1 2 − 2 ∗ 2 1 ( 1 + 3 ) ∗ 1 ∗ 2 3 . = 2 1 ⟹ M C = 2 1 . U s i n g S i n R u l e t o f i n d ∠ C M D , M C S i n M D C = 1 S i n C M D ⟹ S i n C M D = 2 1 2 1 = 2 1 . ∴ ∠ C M D = 4 5 o .
use co-ordinate geometry. Take A as origin, AB as X axis. points X,B,D are co-linear. slope of MC =1 hence required angle=45 degree
Here are my steps:
- Draw hexagon with square attached.
- Extend the side XB of the square that intersects with two vertices of the hexagon. This line XD creates a triangle △BCD with two of the hexagon's sides. Let's assume the hexagon's side lengths are 1 unit.
- Calculate the longer side of the triangle △BCD using trigonometry.
- Add 1 unit to the calculated length because XB = BC = CD , XB = 1 unit.
- Calculate midpoint M by dividing the line XD by 2. We now have a triangle △CMD .
- We now know the length of line DM, the length of the line CD (1 unit), and the angle ∠CDM .
- Use trigonometry to figure out the angle ∠CMD = 45˚.
First, note that D , B , and X are colinear: since A B C D E F is a regular hexagon, D B is an altitude of the hexagon, and therefore is colinear with point X since ∠ D B A + ∠ A B X = ∠ D B X , which is 9 0 ∘ + 9 0 ∘ = 1 8 0 ∘ .
Without loss of generality, let B C = 2 . Now draw the center of the hexagon as point O , draw equilateral triagles B O C and D O C , and let B D intersect O C at K . We can see that B D composes the altitudes of triangles B O C and D O C , and therefore, B D = 2 3 . Since M is the midpoint of D X , D M has length 1 + 3 . Also notice that K M = D M − D K = ( 1 + 3 ) − ( 3 ) = 1 , so, since C K = 1 and ∠ C K M = 9 0 ∘ , Triangle C M K is a 45-45-90 degree triangle. So finally, since ∠ C M K = ∠ C M D , ∠ C M D = 4 5 ∘ .
Take point Z on line AB such that BCZ is equilateral. Now CM is a midline in DZX so CM||ZX. Obviously angle ZXB = 45.
Since A B C D E F is a regular hexagon, and A X B Y is a square, then B lie on a line D X . Suppose that D C = a . Then D B 2 = D C 2 + B C 2 − 2 . D C . B C . cos 1 2 0 ∘ Means that D B = a 3 . So D M = 2 D B + B X = 2 3 + 1 a Let N be the midpoint of D B . Then D N = 2 a 3 . So M N = D M − D N = 2 a 3 + a − a 3 = 2 a Since C N = 2 a , then ∠ C M D = tan − 1 M N C N = tan − 1 1 = 4 5 ∘