Square on the grid
On the regular grid below, four line segments form the pink square. What is its area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
△ A B C ∼ △ D F E ?
Log in to reply
∠ A B C = ∠ D F E and ∠ A C B = ∠ D E F = 9 0 ∘ .
Log in to reply
I wasn't asking how it was true, I was pointing out a very minor typo in an otherwise excellent answer :-)
How do you know DF == 10?
Log in to reply
It is given that the grid square has a side length of 10. And D F is parallel to the horizontal side of the grid.
How did you get $\lt DEF = 90$?
Log in to reply
It is given that it is a pink square. It is a square grid. When you turn the x - and y -axes with the same angle, the two sets of parallel lines remain perpendicular.
Log in to reply
Oh okay, I thought it might have been a Rhombus. <insert self-derisive laughter>
I think a \ is missing before "triangle". Otherwise thanks for the solution.
Thanks for the solution
Proof of triangle similarity?
Awesome!:)
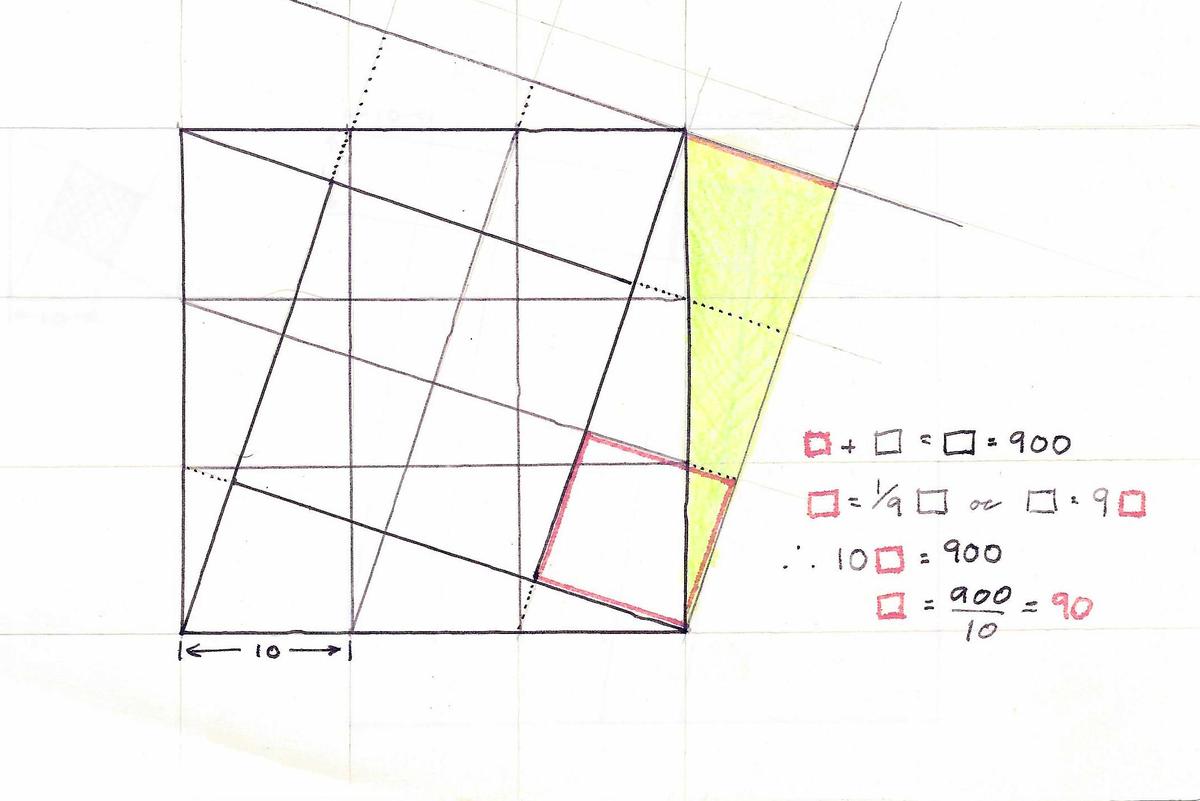
X = DISTANCE BETWEEN DOTS X = 10. 10 X 10 = 100 (There are nine equal squares, making one large square, a 30 X 30 equaling 900) Just 1/9 (or one small square) = 100 Since the lines are offset and parallel equally, the distance between the points is also equal. The size of the "new" square is the same as any of the original nine. The correct answer is 100. A = x2 = 10 X 10 = 100
DF=10 is the key pickup.
very elegant solution! I've added some more solution strategies to add to the point that this problem enables a wide variety of solution strategies.
Figure 1 ( at PhotoBucket ) the problem geometry: Fig 1
Figure 2 ( at PhotoBucket ) the problem solutions: Fig 2
The difficulty level of this problem is NOT really "Basic." It should be under "Intermediate" instead.
The drawing shows a square of area 3 0 × 3 0 = 9 0 0 .
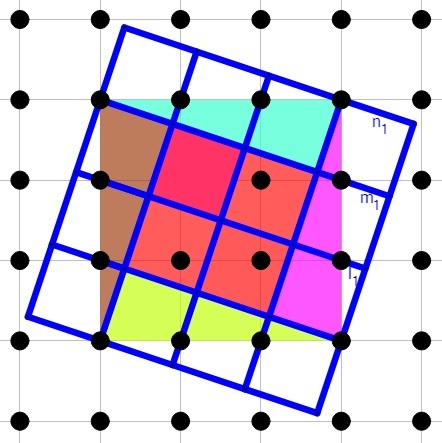
Continuing the pattern of diagonal lines, we obtain four squares in the center (the pink square is one of them), and 12 parts of squares along the edges. These 12 parts can be paired up to form another six squares. Thus the diagonal pattern divides the area into 10 squares of equal size. The area of each such square is 1 0 9 0 0 = 9 0 .
Moderator note:
To illustrate this answer, I have added some extra lines and counted the 10 squares. When the same number appears twice the matching parts form a square.
That's still confusing to me
The problem I see with this question is the lines are parallel spaced at a distance of ten which means the side of the square is exactly 10, slanted yes but since parallel lines are evenly spaced it is x=10 now since the intersecting lines are perpendicular at the same distance of 10 again parallel. Which we have a perfect square with sides spaced at the distance 10 now I can see if this square was not a square and if the lines were not perpendicular and parallel.
Log in to reply
The distance between lines should be measured in perpendicular direction. It is true that the spacing between the lines is still 10 when measured horizontally, but when measured perpendicularly it is slightly less: 3 0 / 1 0 .
Words are above, and it is Brillant
Words would be helpful.
To solve for the area of the square, all we need to do is find the length of one side and then square that length.
I defined the square as square ABCD, where A is the top most point, B is the right most point. C is the furthest down point, and D is the left most point. I then defined the top left dot of the grid as being coordinate (0,0). To determine the length of side AB, we will need to find the coordinates of A and B. Once we have the coordinates, we can use the Pythagoras Theorem to find the length of line segment AB is the square root of the sums of the square of the distance between the two X coordinates and the square of the distance between the two Y coordinates. Furthermore, since we will then be squaring that number to find the area of the square, we can skip finding the square root.. (Yay! I love skipping steps!)
We can find the coordinates of A by finding the point-slope equation of AB and the point-slope equation of AD, then calculating where they intercept. Doing the same for AB and BC gives us the coordinates of B.
To find the point-slope, we need to calculate the slope and find a known coordinate of the line, then use the point-slope equation y − y1 = m(x − x1), where m is the slope and (x1,y1) are known coordinates of the line.
The slope of AB is the distance it travels upward (-10 units) divided by the distance it travels to the right (30 units), which simplifies to \frac {-1}{3} . We have two easy to determine coordinates, (0,0) and (30,-10) but for simplicity I used (0,0) The point-slope equation is therefore y - 0 = \frac {-1}{3} * (x - 0), or y= \frac {-1}{3} x.
The slope of AD is the distance it travels upward (30 units) divided by the distance traveled to the right (10 units) or 3. We have (0,-30) and (10,0) for coordinates. Using (10,0) we have (y - 0) = 3 (x - 10) or y=3x - 30.
The slope of BC is identical to AD, and we have (10, - 30) and (20, 0). Using (20,0) we have (y - 0) = 3 (x - 20) or y=3x - 60.
The intercept of AB and AD is where \frac {-1}{3} x = 3x - 30. Multiplying both sides of the equation by -3 gives us x = -9x + 90, or x=90 - 9x.Adding 9x to each side of the equation brings us to 10x = 90, which we then divide both sides by 10 to get x = 9.
To get y, we just take the x coordinate (9) and run it through either the point-slope equation of AB or the point-slope equation of AD. When x is 9, -(1/3)x and 3x - 30 both equal -3, so y=-3 and the coordinates for A is (9, -3).
The intercept of AB and BC is where \frac {-1}{3} x = 3x - 60. Multiplying both sides of the equation by -3 gives us x = -9x + 180. Adding 9x to each side gives us 10x = 180. We then divide both sides by 10 to get x = 18.
Using the point-slope equations AB and BC, we get \frac {-1}{3} x and 3x - 60 both equaling -6, so that the coordinates for B is (18, -6).
Good old Pythagoras lets us know the distance between point A (9, -3) and point B (18, -6) is the square root of the sums of the square of (9 - 18) and the square of (-3 - -6). 9 - 18 equals -9, which become 81 when squared. (-3 - -6) is equal to 3, which becomes 9 when squared. Line segment AB is thus the length of the square root of (81 + 9) units long. We COULD actually run this through a calculator to find the numerical value of \sqrt{90} , but we don't have to. Since we know that ABCD is a square and thus the area of ABCD is the length of any side of that square multiplied by itself, we take the square root of 90 times the square root of 90 to get.... 90 units!
This is also the method I used.
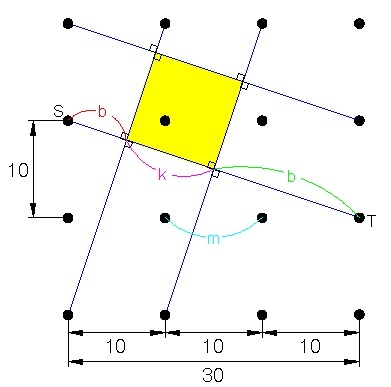 From my figure,
From my figure,
2 0 m = 3 0 1 0 ⟹ m = 3 2 0
and by pythagorean theorem, we have
S T = 1 0 2 + 3 0 2 = 1 0 1 0
and
1 0 1 0 3 0 = 3 2 0 + 1 0 a ⟹ a = 5 1 0
then
1 0 1 0 = 2 0 b ⟹ b = 2 1 0
it follows that,
k = 1 0 1 0 − 2 1 0 − 5 1 0 = 3 1 0
Finally, the area of the shaded region is
A = k 2 = ( 3 1 0 ) 2 = 9 0
I used linear algebra and made the origin the bottom left dot and i made equations of the corresponding line segments in vector form> Now because it is a square that is formed, you only have to find the intersection of one line with the two parallel lines (in this case i choose) (r1 is the line from the bottom leftmost to the top 2nd dot, r3 is the downward line segment from top left dot and r4 is the line below r3 (moving parallel to r3).
r1= t(10,30)
r3=(0,30)+s(30,-10)
r4=(0,20)+u(30,-10)
Now using parametric equations
r1: x=10t y=30t
r3: x=30s y=30-10s
r4: x=30u y=20-10u
Now find the point of intersection between r1 and r3
x(r1)=x(r3) y(r1)=y(r3)
10t= 30s 30t= 30-10s
t= 3s. ---> plug in 3s 30*3s = 30-10s
making s= 3/10
the POI for r3 and r1 (9,27) **
x= 30s= 30 (3/10)= 9 y= 30-10 (3/10)= 27
Do the same for r1 and r4
r1= t(10,30)
r4=(0,20)+u(30,-10)
r1 (in parametric form):
x=10t
y=30t
r4 x=30u y=20-10u
x(r1)=x(r4) y(r1)=y(r2) 10t=30u 30t= 20-10u t=3u ----> 30*3u= 20-10u solve for u and u= 1/5
plug in u to find x x=30u= 30 1/5= 6 y=20-10 1/5= 18 * The poi for r1 and r4 is (6,18)
Now find the distance between (9,27) and (6,18) using the following formula
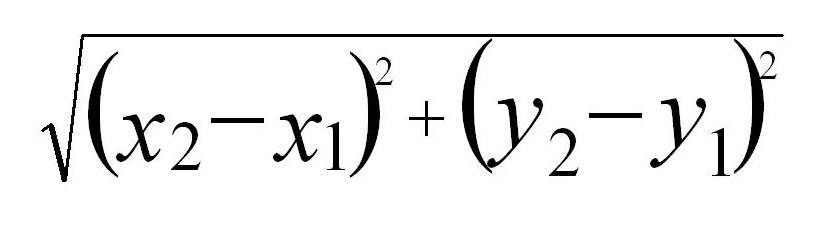 The resulting distance should be sqrt(90)
The area of a square is the sidelength^2 = sqrt(90)^2= 90
Therefore the area is 90.
The resulting distance should be sqrt(90)
The area of a square is the sidelength^2 = sqrt(90)^2= 90
Therefore the area is 90.
I was really pleased with this:
Let the sides of the pink square be x . From the figure above, where D F ∣ ∣ B C , we note that △ A B C is similar to △ D E F . Therefore,
D F E F 1 0 x ⟹ x = A B B C = 1 0 2 + 3 0 2 3 0 = 1 0 3 0
The area of the pink square A = x 2 = 9 0 .