Square Roots With Fractions?
y x × z y × x z
If x , y , and z are positive numbers, then what the value of the expression above?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
We know:- b a = b a
⇒ y x × z y × z x
= 1
easy pizy.
Log in to reply
Not that easy.If x = − 1 , y = 2 , z = − 3 , the answer is ( − 1 ) .
Log in to reply
you need to plug number and check, do the algebra
Log in to reply
@Mardokay Mosazghi – It must be mentioned that x , y , z are all either positive or negative. Otherwise the answer is 1 or − 1 .
You are right Nihar. Also, what if x or y or z = 0 ?
Log in to reply
@Arulx Z – The question has been edited and now x , y , z are restricted to only positive reals.
Do read the N.B. ?? Please read the N.B.
Log in to reply
@Vubon Roy – That NB was put 2 days after I commented this.
The variables are understood to equal to 1
x=4 y=2 z=1 becomes 2 x 2 x .25 = 1
Moderator note:
You have only shown that the expression equals to 1 when x = 4 , y = 2 , z = 1 . But you should in fact show that the expression equals to 1 for all positive numbers x , y and z .
√(x/y) * √(y/z) * √(z/x) = √(xyz)/(yzx)
Since xyz=yzx we can find that (xyz)/(yzx)=1 which means that √(xyz/yzx) = √1 = 1
(Sorry there's no formatting, I wasn't sure what I was doing wrong while trying to add it)
how do you know that the result of this equation is 1
not right they can be anything at all
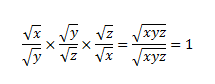
y x × z y × x z = y x × z y × x z = 1 = 1