Maximizing These Squares?

Probability Level 3

You are given three squares of equal size. What is the maximum number of squares that can be formed out of them by overlapping them in any way possible?

7 8 9 10

1 solution

Abhay Tiwari
Apr 15, 2016

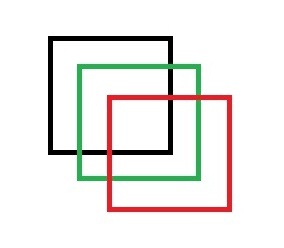This is the best possible way, forming eight squares.

How do you know that we cannot form 9 or more?

Calvin Lin Staff - 5 years, 2 months ago

Sir to form a square out of two square, the two of them should cut each other twice, that is, they should cut each other's side twice(then a new square is formed with two sides from one square and two side from other square).

Now when we have three square, then maximum number of squares are possible when all of them cut each other twice, then the above mentioned figure is one of the way to do it.

Abhay Tiwari - 5 years, 2 months ago

... is one of the way to do it?

Are you saying that there are other configurations that produces 9 or more squares?

Pi Han Goh - 5 years, 1 month ago

@Pi Han Goh – I am saying that there is other ways to check maximum number of squares, that is by simply making configurations, but that is a lengthy one.

Abhay Tiwari - 5 years, 1 month ago

@Abhay Tiwari – Other ways? Meaning? Proof by exhaustion?

Pi Han Goh - 5 years, 1 month ago

@Pi Han Goh – yes, by trying each and every possible outcome.

Abhay Tiwari - 5 years, 1 month ago

@Abhay Tiwari – And how many possible outcomes are there? 100? 2000? 10000000?

Pi Han Goh - 5 years, 1 month ago

@Pi Han Goh – Seeing the problem I don't think there are more than 3 or four outcomes which forms square with the use of each and every square given at hand, which anyone can think of. Otherwise there can be millions of outcomes without the formation of squares. Pi han goh, Please provide solution to your statement problems, I was not able to do some of them. I have some doubts in those problems. Post the solution.I will ask then.

Abhay Tiwari - 5 years, 1 month ago

Maximizing These Squares?

1 solution

0 pending reports