Square Wire Moment
Consider a square wire with side length L , total mass M , and uniform mass density. Determine the wire's moment of inertia about an axis lying in the plane of the square and coinciding with the square's diagonal.
If its value can be represented as α M L 2 , determine the value of α .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is precisely how I solved it! Starting with the moment of inertia of a rod about its center, and then moving on to given setup by making use of the symmetries in the square and its diagonal.
I am thinking, can we use this method to find the moment of inertia of a general rhombus about its diagonal? Will all rhombuses of the same sidelength have the same moment of inertia about its diagonal?
Log in to reply
Yes, I agree with you, their diagonals should have an equal moment of inertia. Moreover, the diagonals of rhombus are orthogonal, therefore, we can also use the perpendicular axis theorem.
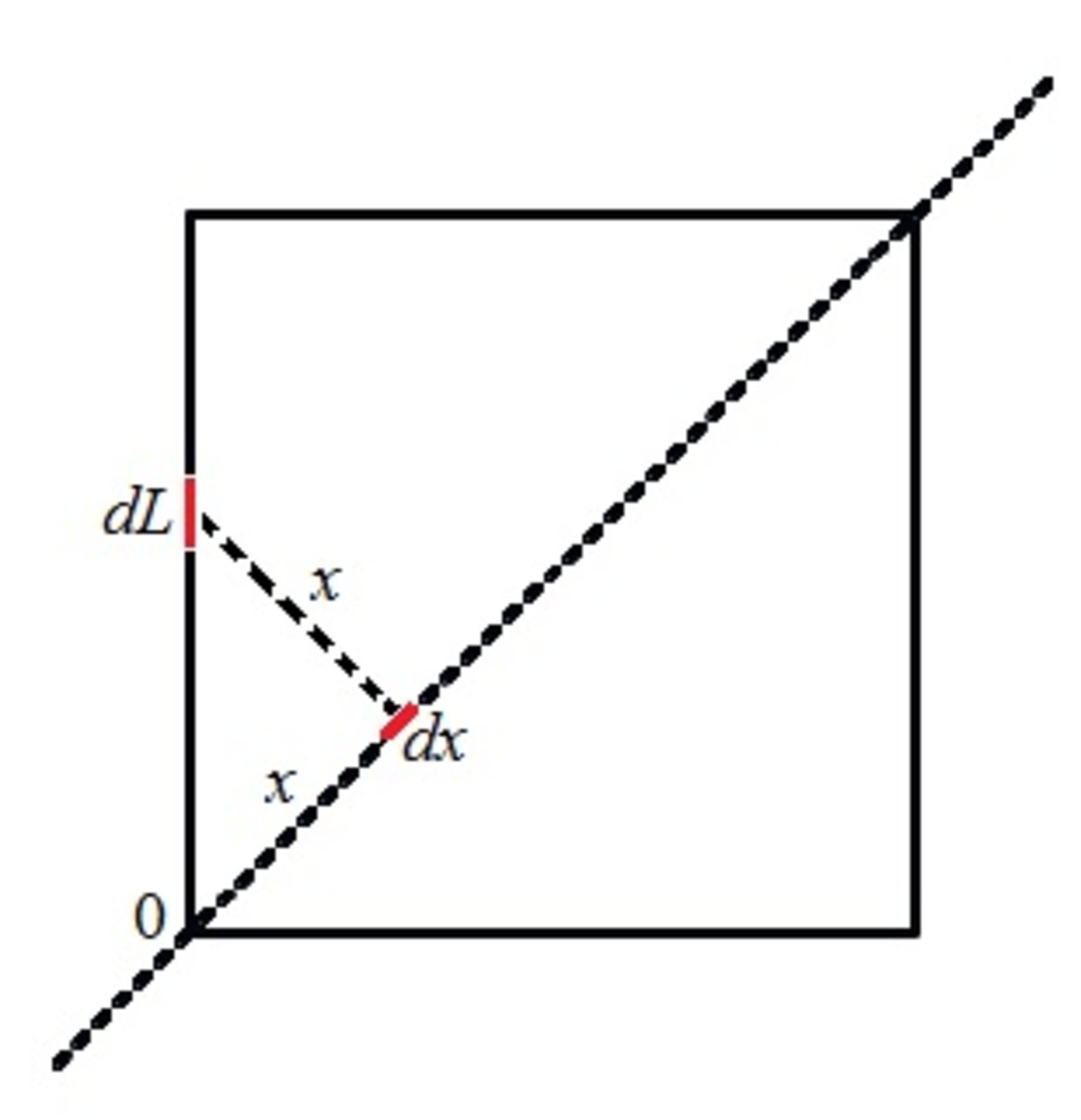
Let the diagonal be the x -axis with 0 at the lower end and the mass per unit length of the square be σ , the moment of inertia of the square is as below:
I = 4 ∫ 0 L x 2 σ d L = 4 ∫ 0 2 L 2 σ x 2 d x = 4 ∫ 0 2 L 4 L 2 M x 2 d x = ∫ 0 2 L L 2 M x 2 d x = 3 L 2 M x 3 = 6 M L 2 Note that d L = 2 d x Note that σ = 4 L M
⟹ α = 6 .
I agree with Tapas. Using this basic definition of the moment of inertia, I = ∫ r 2 d m , we can find the moment of inertia of general shapes, where it is difficult to find symmetries.
Done with the basics! :)
Log in to reply
Was too easy didn't expect to be in level 5
Log in to reply
Yes. I have the same thoughts @Sahil Silare . Btw, I solved your double summation problem and texted you a solution. Check it out.
From the symmetry of the figure we can say that the wire frame has equal moment of inertia about its two diagonals A C and B D .
Also, these diagonals are orthogonal therefore, according to the Perpendicular axis theorem. I O = I A C + I B D . Here, I O is the moment of inertial of the wire frame about an axis passing through the center O and perpendicular to the plane of the wire frame. Also, I A C = I B D . Therefore, we can write I O = 2 I A C . The four wires will have equal moment of inertia about the axis passing through O and perpendicular to the plane of the figure. Therefore, the moment of inertia of the complete wire frame about this axis can be calculated by finding the moment of inertia of one of the wire and multiplying it by 4. The moment of inertia of the wire A B about the axis passing though its center of mass and perpendicular to plane of the figure is
I cmAB = 1 2 M AB L 2 = 4 8 M L 2 . The moment of inertia of A B about the axis passing though O can be calculated using the parallel axis theorem. I O A B = I c m A B + M A B d 2 . Here, d is the distance between these two axis. Hence,
I O A B I O A B I O I A C I A C I A C α = 4 8 M L 2 + 4 M ( 2 L ) 2 = 1 2 M L 2 = 4 × I O A B = 3 M L 2 = 2 1 × I O = 6 M L 2 = α M L 2 = 6 .