Squared
On the 4 × 4 board above, each tile is colored orange on one side and blue on the other. With each move, you must flip one of the following: (1) an entire row, (2) an entire column, (3) an entire diagonal, or (4) all four corners.
After some number of moves, can you make the whole board orange ?
With each move, you must flip a row, column, diagonal, or flip the four corners.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
It is possible, but why is it possible? Can you evaluate it without trying it? Assume it is a n x n board with x showing orange. Has it something to do with parity?
Log in to reply
Well, surely, if n is even, the number of orange squares must have the same parity as the number of total squares, as each move can't change the parity of the number of orange squares. I would guess that every position that does satisfy this property is achievable as there are so many ways to move them around, but I have no proof.
This may not answer your question, but here are a few observations concerning parity to think about:
If we label the grid as follows with A's, B's, C's and D's, then each allowed move (horizontal line, vertical line, diagonal line, or 4 corners) covers exactly 1 A, 1 B, 1 C, and 1 D:
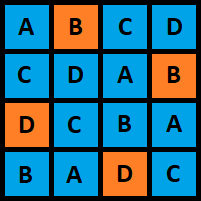
If we choose a move with an A, B, C, and D set with 4 blues and 0 oranges, all 4 blues will change to oranges, for a net increase of 4 oranges. If we choose a set with 3 blues and 1 orange, all 3 blues will change to 3 oranges, but 1 orange will change to blue, for a net increase of 2 oranges. If we choose a set with 2 blues and 2 oranges, the 2 blues will change to 2 oranges, and the 2 oranges will change to 2 blues, for a net increase of 0 oranges. If we choose a set with 1 blue and 3 oranges, the 1 blue will change to orange, but the 3 oranges will change to 3 blues, for a net decrease of 2 oranges. And we choose a set with 0 blues and 4 oranges, all 4 oranges will change to blues, for a net decrease of 4 oranges.
This means that for any move we choose, the total number of orange squares on the board changes by an even number. So if we started with an odd number of orange squares, we could conclude that it is impossible to reach 16 orange squares. But we started with an even number of orange squares (4) so all we know from this theorem is that it might be possible to reach 16 squares .
A second observation is that if we take away the 4 corner move, then the number of orange squares in each of the four 2 x 2 quadrants (see below) keeps its parity from start to finish .

For example, in the starting board of the question, there are an odd number of oranges in each of the four quadrants (1). Any move using a vertical, horizontal, or diagonal line will still keep an odd number of oranges in each quadrant. (The proof for this can be left as an exercise for the reader.)
We can then conclude from this second theorem that to change the starting board of the question with an odd number of oranges in each quadrant (1) to an even number of oranges in each quadrant (4), we must use the 4 corner move at least once to change the parity of each quadrant from odd to even.
Log in to reply
Notice that the second observation is simply a generalization to a 2x2 grid with only vertical, horizontal, and 1 diagonal moves.
After some Python brute force, there are 2880 solutions with 6 moves, but there are all the permutations of only 4 disctinct set of moves (with h for horizontal move, v vertical, d diagonal and c corner):
- h1,h2,v2,v4,d1,c
- h1,h3,v1,v2,d2,c
- h2,h4,v3,v4,d2,c
- h3,h4,v1,v3,d1,c
If you look closely, you can see that the four solutions are in fact only one solution, after the 4 possible rotations (due to the specific initial state), so there is truly only one solution.
And more interesting, I found no solution if you force 7 moves! (not allowing for the obvious "do nothing"). I'll check my code, but I found that quite interesting... I'd like to check higher number of move but my laptop was already quite slow with the 7 moves, i need to optimize my code.
Log in to reply
That's really surprising about no solution for 7 moves. Good find!
Log in to reply
If you look at the four pairs of edge pieces and the number of moves required to make them each orange you can find a relationship between groups (v1,v4,h2,h3) and (v2,v3,h1,h4) which forces 4 of those moves to be odd in number.
Without loss of generality we can make those moves first in any sequence as you have done. A solution with 7 steps would require a 3 step solution from your diagram 5 which is impossible out of the remaining diagonal or corner moves
can u send the code?
Log in to reply
@Mannan Bhola , sure! (sorry for the vacations delay!) do you have any medium/format would like to receive it through/for? It's in Python 3.
I made a little game out of this. I'm very new to programming, so it's very rough. I'm commenting here because I don't know how to post my new solution. https://tile-game.herokuapp.com/tileGame.html
Log in to reply
The game replicates the model well although there are a few spelling mistakes
I encourage anyone who wants to seek fun in this problem to play the game
you have wrong operation order... you must first flip a row right rather than a column for the initial configuration, it doesn't matter sinice intial configuration is symmetric respective column or raw you have selected firstly? and similar operation following consecutively is n't it violating the 1,2,3,4 order?
Log in to reply
It sounds like you misunderstood the question; you may use any operation whenever you like.
I wrote a very simple script that computes the distance from the initial configuration to to all reachable configurations. There are only 512 reachable configurations and the greatest distance, including that to the desired target configuration, is 6 moves.
That means, there are quite a few invariants. An obvious one is the number of tiles of each color, which is always 0 mod 4. That cuts the size of the configuration space from 2^16 (65,536) down to 2^12 (4,096). Other invariants are imposed by the symmetries in the set of available moves.
I confess I originally got this problem right by a lucky guess, but then my consciousness shouted "hey, that's not how we do things!" in full volume. I knew I had to do something about it, so that my solution to this problem was not a mere coin flip. After a short time searching for a sequence of instructions that worked, I managed to come up with the following solution. I hope you will pardon my less than stellar graphic editing skills.
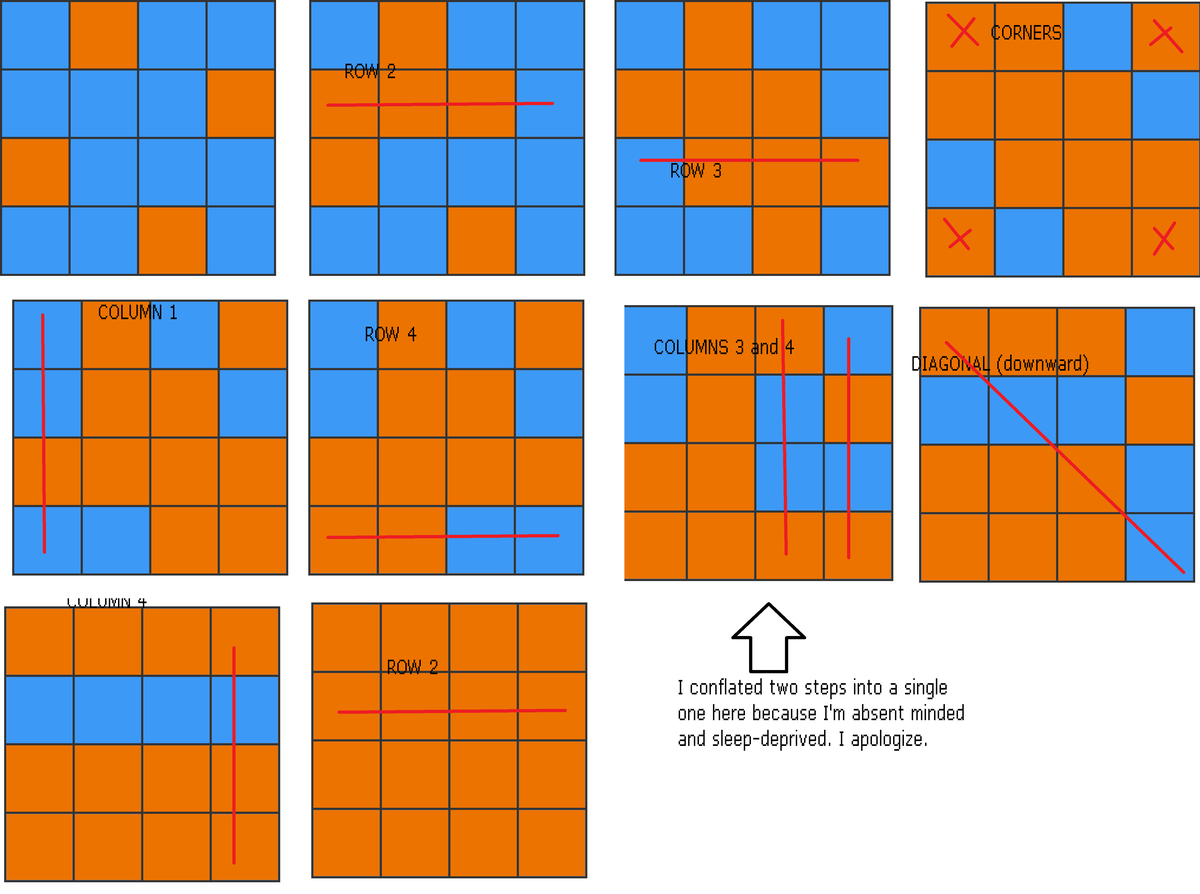
For a strange reason, this kind of problem is really satisfying to solve. I recommend you all spend some time looking for different solutions, it's really neat when you find a pattern that works. Sure, the ad hoc sleep deprived musings of my grad student self did not yield a particularly efficient solution, as there is a better one already posted here, but I'd love to see what you all come up with. In fact, it makes me wonder how many solutions exist for each number of steps... could that be a potentially interesting puzzle? Well, who knows. Maybe I should get some sleep, bye.
Is there a reasoning method rather than showing example approach for this problem?
Log in to reply
Not really, unless you count a 16x11 matrix as a reasoning method.
Basically, you make a matrix where each row is one of the possible moves and each column is one of the fields. You put a 1 if that move flips that field, and a 0 otherwise. Add a row with the starting position. Then, you use modulo-2 to 'solve' the matrix (gaussian elimination) but don't use the last row. If you put the identity matrix next to it and update that while solving, you get the solution.
But that's just a clever way to brute-force it.
Since flipping the same row/column twice is the same as doing nothing at all, (step 1 = final step = row 2) and (step 6 = step 8 = column 4) seems redundant. Removing these results in 6 moves, which is optimal.
Each flipping operation leads to increase in some blue squares and decrease of orange squares. May be we can use infinite series to solve this. I feel we can killl these problems using some generating series type ideas. I got a wrong answer. The reason is I am tired and did not sleep properly yesterday.
If the method I posted is general, then we can calculate the number of ways to solve. It involves selecting two of four possible preexisting blue squares that are impacted by only two operations. So 4 choose 2 = 6 choices of four moves. Then I believe probably there is always the need to do a diagonal and corner move. So there are 6 unordered distinct sets of 6 moves. Ordering each involves multiplying by 6!=720. So I think there are 6*720=4320 solutions. This is just a quick guess. There may be other ways of solving different than my method and maybe some instances of my method do not require both a diagonal and corners move, which could change the answer.
Nice solution! It took me very long to actually come up with a solution for this problem, because I tried to prove there wasn't one! ONe comment though, the order of your steps is always irrelevant, so you flipped the second row twice for no reason :p (Also the fourth column). If you take these 4 steps away, you arrive at the optimal number of steps (which is six).
My solution is quite similar to David Vreken. Due to symmetry, we can rotate and translate the steps on the board, as well as change the order of steps.
The question now is: what is the minimum number of steps?
Clearly less than 4 is inadequate. But what about 4 or 5 steps? It seems improbable, but we can’t be sure yet. I’ve tried to number the tiles in chessboard fashion, but my approach involved considering so many cases that I gave up.
What do you think?
After thinking about your problem for a while, I think I’ve proved 6 the minimum. 6 is clearly sufficient, as David Vreken’s solution shows. Less than 4 is clearly impossible, so all I need to show is that 4 and 5 are impossible. The first important realisation I had was that a solution, at minimum, has to hit every initially blue space at least once. This immediately rules out 4, since the only way to do this with 4 moves is four horizontal (or vertical) lines, and four horizontal lines is clearly not a solution. The proof of five impossible is a little trickier, but thinking about hitting all the blue squares led to a second realisation: squares on the edges (not the corners) can only be flipped by two lines, one vertical, one horizontal. Since the four blue edge tiles aren’t in line with each other, they each require one line. This gives 16 cases (depending on whether you use a line along the side or across the middle), which are really 6 cases thanks to rotational symmetry. Each case is then easily checked: none of them leave a set of squares which can be flipped in less than two moves. So, 6 is both sufficient and minimal. QED.
Log in to reply
How about the type of moves? Are they all the same type, but different orders or are there different combinations?
Log in to reply
I’m not positive I understand what you’re asking. If your question is about properties of the six step solutions, I would point you towards the comment section for David Vreken’s answer. The purpose of my response was simply to show that no solution in less than six steps is possible.
@Thomas Lesgourgues wrote a computer program that matches your reasoning. (See comment section in my solution.)
Log in to reply
Thanks for the heads up! I’m glad to see experimental proof as well as logical proof.
In David Henderson's solution, you can see that all efficient solutions are 6 steps.
He points out that the sequence of moves doesn't matter, and that repeating a move is pointless since it only undoes the previous time. Because of this, any search for a solution need not consider repeated moves - only whether a move is applied or not. His exhaustive search found 4 combinations of moves and that all solutions required 2 rows, 2 columns, 1 diagonal and all 4 corners to be flipped.
Knowing that repeated moves undo themselves, it can be seen that including inefficient solutions that include repeated moves, all solutions will have an even number of steps.
I'd be interested to know if there is a way to derive this without an exhaustive search but I have no idea where to start with that.
A solution with a lot of symmetry in 6 steps
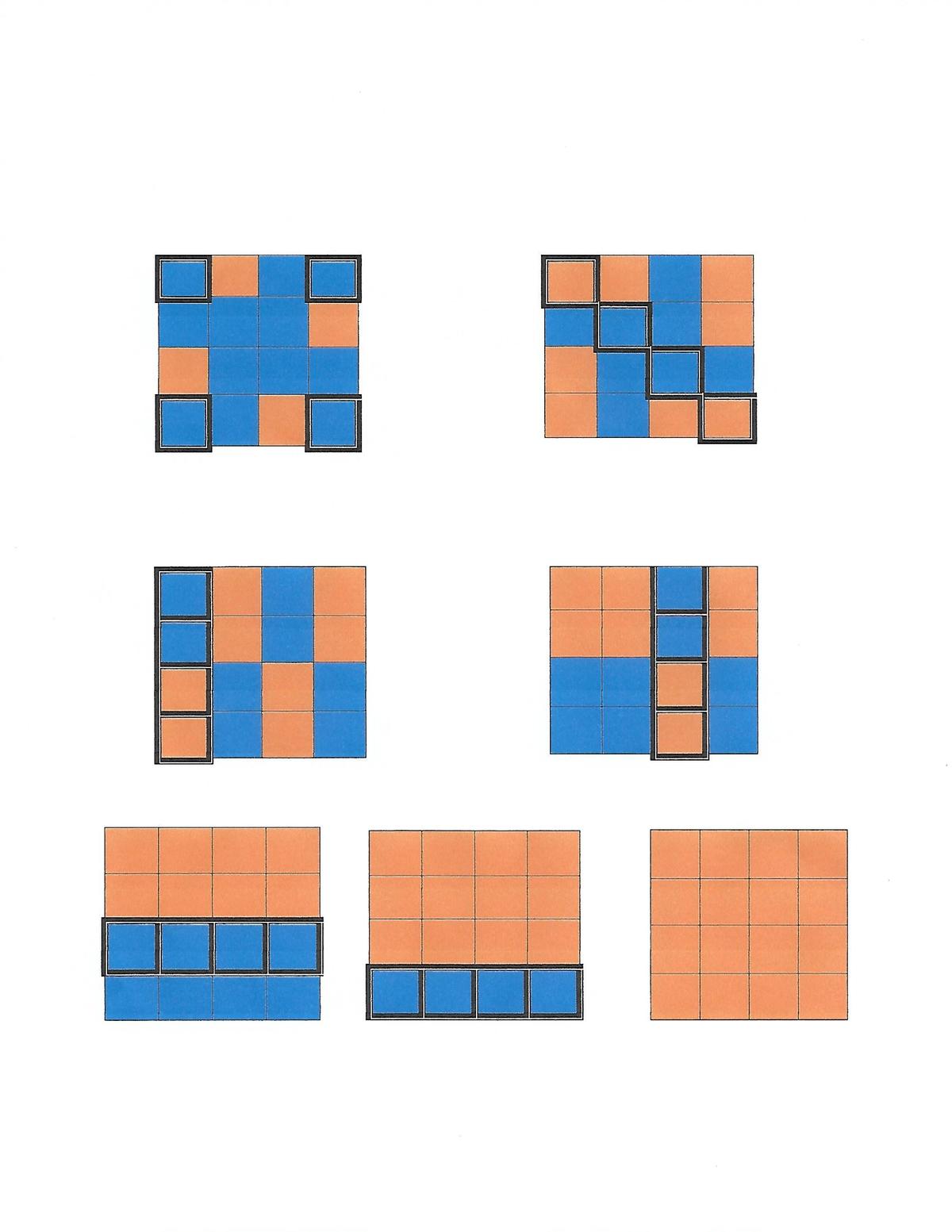
Another solution in six steps . Following the advise of Iskander and Eric, I removed step2 and step 6 to improve my original solution( the third one**). Thanks!!!
Better version of my original solution
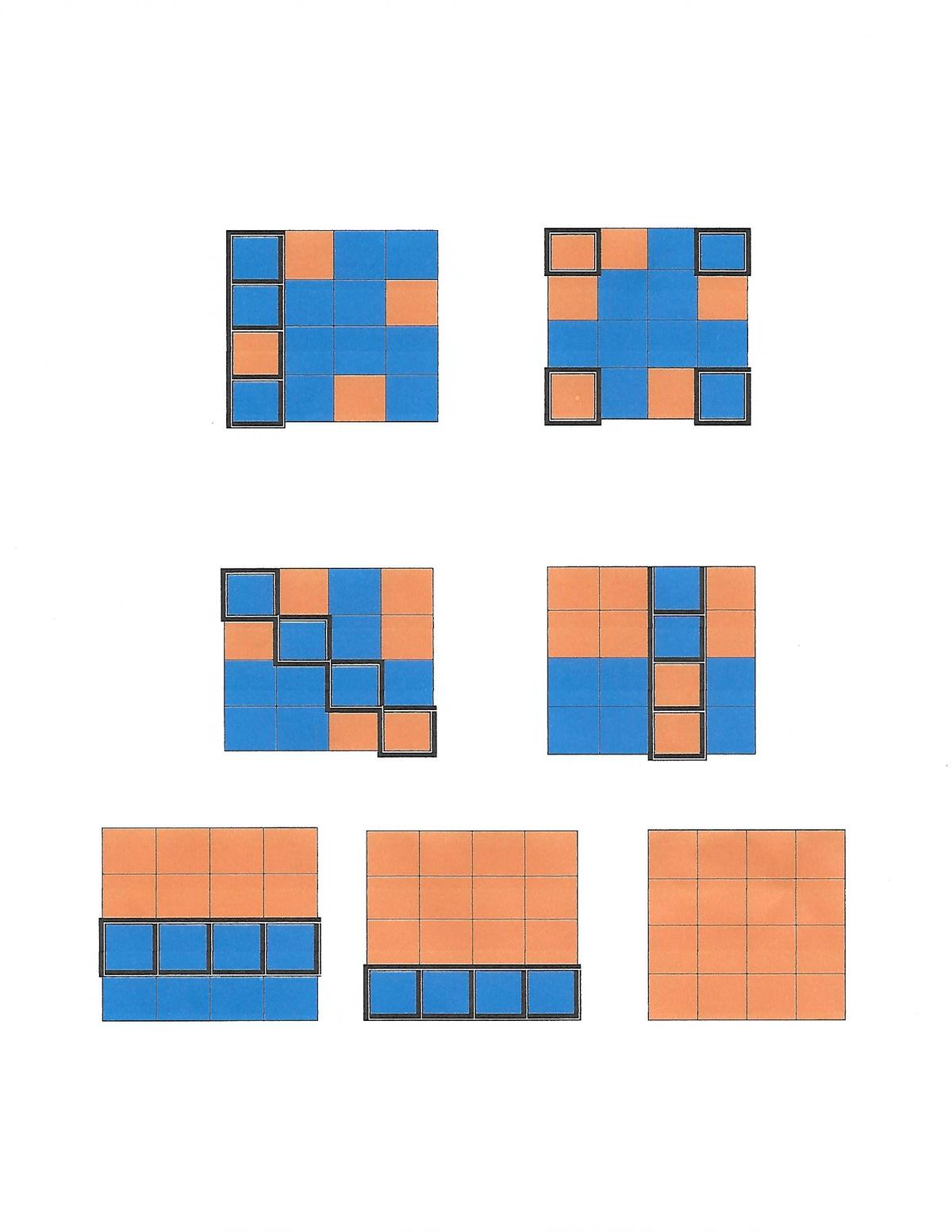
My original solution
step 2 and 6 cancel out, they're redundant
Log in to reply
Hi. In both steps we work with column 4 but the steps do not cancel each other. In step 2 we work with 3 blue squares, in step 6 with two blue squares.
Log in to reply
Sure they do. Although it might be prettier, you could skip both steps 2 and 6 and have the same solution, but faster.
Log in to reply
@Eric Valpey – I agree!!! I'm eliminating steps 2 and 6, to get a shorter solution!!! It's already posted!!! Thank you!!!
There are four unique moves which each give an all-orange board:
- Rows 3 and 4, Columns 1 and 3, four corners, and backslash (\)
- Rows 1 and 2, Columns 2 and 4, four corners, and backslash
- Rows 1 and 3, Columns 1 and 2, four corners, and forward slash (/)
- Rows 2 and 4, Columns 3 and 4, four corners, and forward slash
The technique I used was to consider that there were eleven possible moves, and that repeating a single move would undo that move (even if there had been other moves in between), the only question is whether or not a particular move was made. Since there are two states for each of those 11 possible moves (rows 1-4, columns 1-4, four corners, backslash, and forward slash), we only needed to consider 2 1 1 different combinations. In binary, these could be designated as 0 0 0 0 0 0 0 0 0 0 0 (no moves made) through 1 1 1 1 1 1 1 1 1 1 1 (every possible move made).
I iterated through the numbers 0 through 2047, applying the selected moves when considering the number as binary digits. There were four combinations that produced an all-orange board were 860, 931, 1333, and 1482. Those are 0 0 1 1 1 0 1 0 1 1 0 , 1 1 0 0 0 1 0 1 1 1 0 , 1 0 1 0 1 1 0 0 1 0 1 , and 0 1 0 1 0 0 1 1 1 0 1 .
because parity! :-D
what I mean: no matter which of the moves you make, if the number of orange tiles was odd, then it will be odd afterwards too.
for example. it was 1 orange in a 4 tile field, then flipping makes it 3 oranges.
1 is odd, 3 is odd.
another example: 0 oranges becomes 4 oranges after flipping. both even numbers.
since this is then obviously true no matter how many moves you make, it is also obvious that you can only ahieve a number of orange fields with the same parity as in the beginning.
so if it was 5 oranges in the beginning, then you can only reach an odd number of orange tiles.
so only, 1,3,5,7,9,11,13,15,17,etc. orange tiles are possible.
so what in our case? 4 oranges ate the start, aka an even number.
the number of fields is 16, so we would need an even number of orange fields too.
so it is for sure possible to fill the board with orange tiles.
while if for example the board had 15 tiles, it would be impossible to fill it completely with orange tiles, no matter how hard you try.
It make sense, but I think your idea only proves the necessity and does not prove sufficiency.Your idea of this quiz can only tell us that there may be a solution, so it still haven't solved the problem.
People like you who help make the world better.
We can imagine the process of flipping the squares. No matter how you flip it, the number of orange squares will always stay odd or even(even in this case). We also see that there are a total of 12 blue squares, which is even, like the number of orange squares. Meaning that flipping the squares to get everything orange is possible. p.s. I have limited knowledge and welcomes questions and corrections from the general public
Every flip flips 4 tiles, so the number of tiles we have to flip has to be divisible by 4 , which it is. This simple proof does not prove that there is a way to flip them all up, but that there can be.
Give each move a label:
r1 through r4 for rows top to bottom
c1 through c4 for columns left to right
d1 for top left to bottom right diagonal
d2 for top right to bottom left diagonal
k for corners
In each cell write the operations that can toggle the cell. Note that finding an all blue solution is equivalent to finding all orange because you can just toggle all rows.
There are 8 cells, including the preexisting orange ones that are only impacted by two operations. These are therefore the most constrained (least degrees of freedom) and must be dealt with first. To get all blue, the four orange ones must have experienced an odd number of operations, while the blue ones must have experienced an even number. Pick both operations that are affected by one of preexisting blue cells (to keep it even) , and then again with another preexisting blue cell.
For example, one blue cell has r1, c3 and another has r2, c1, so choose those four operations. Each operation appears only once in the preexisting orange cells. Thus the 8 more-constrained cells will all be the same color. Evaluate the board after these moves (r1, c3, r2, c1) , and it is easy to see that if you do moves d1 and k, then the whole board will be blue. Add r1, r2, r3, r4 to this to get an orange board. Two of the same operations (ie r1+r1and r2+r2) cancel out, and the order doesn't matter (commutative).
So here is a solution: r3, r4, c1, c3, d1, k
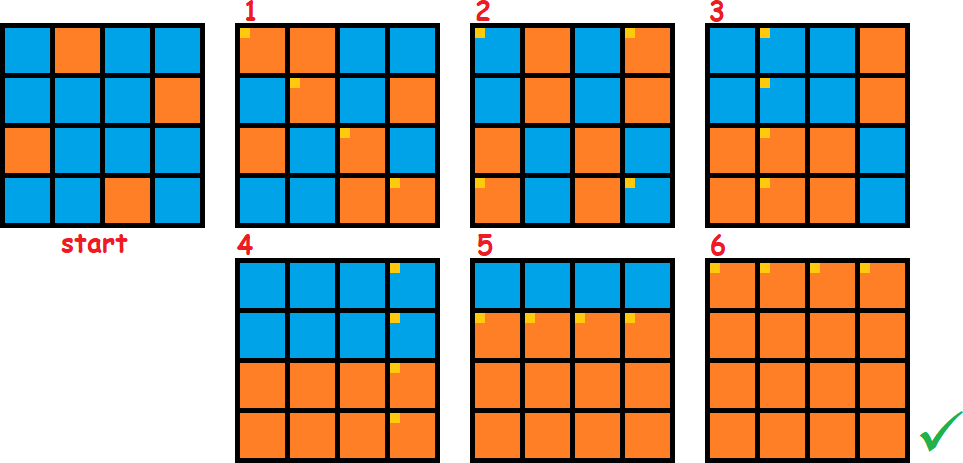
One possible solution: