Squares and Circles
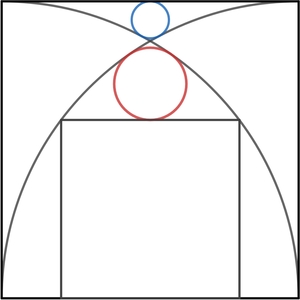
Two circles, two quarter-circular arcs, and a square are drawn inside a bigger square as shown in the figure.
Find the ratio of the radii of the blue and red circles.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
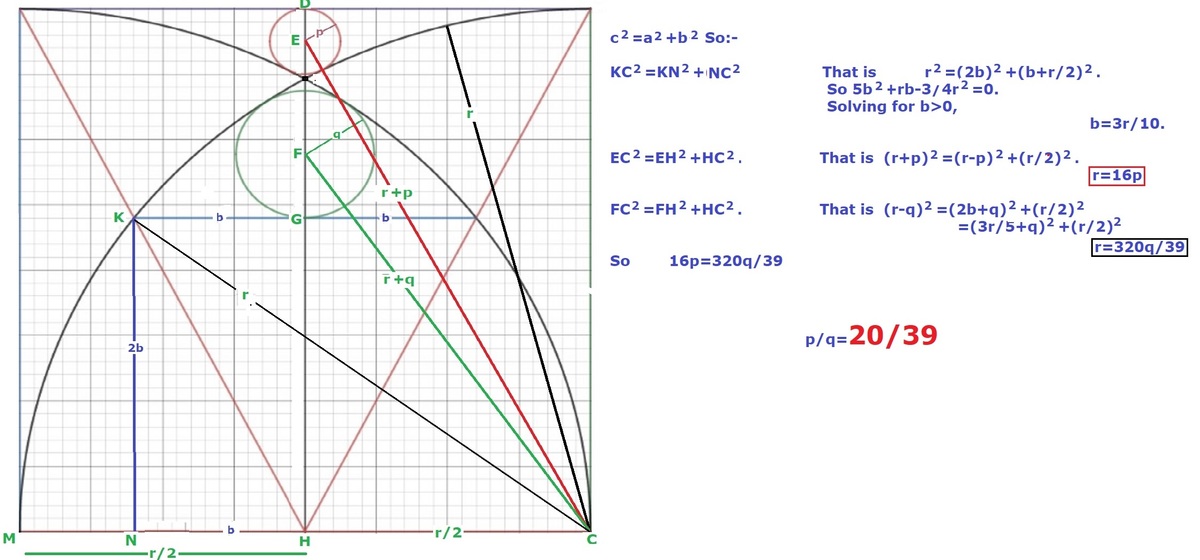
If r is the radius of the blue circle, R the radius of the large quarter circles, s the radius of the red circle, and X the side of the small square (the big square has side R ), then we obtain the following equations ( R + r ) 2 R 2 ( R − s ) 2 = ( R − r ) 2 + 4 1 R 2 = X 2 + 4 1 ( X + R ) 2 = ( X + s ) 2 + 4 1 R 2 which solve to give R = 1 6 r , X = 5 3 R and s = 3 2 0 3 9 R , so that s = 2 0 3 9 r , making the answer 2 0 : 3 9 .
I'm struggling to see how you arrived at any of those three equations...
Log in to reply
For example... The right-angled triangle formed by the centre of the blue circle, the bottom left corner of the big square and the middle of the bottom side of the big square, has sides of length 2 1 R , R − r and R + r . The other two identities are obtained similarly.
Log in to reply
Maybe I'm missing something here, but how do you know that the center of the blue circle, the bottom left corner of the big square, and the point of tangency between the blue circle and the quarter-circle are all collinear?
Log in to reply
@Jordan Cahn – The bottom-left corner of the big square is also the centre of the quarter circle tangent to the blue circle. Since the blue circle and this quarter circle are tangential, they must share the same normal at the point of tangency. Since a normal to a circle is a radius, it passes through the circle centre, so we deduce that the centres of the two circles and their point of tangency are collinear.
Log in to reply
@Mark Hennings – Got it, thanks! Sorry for the brain-freeze... I wasn't thinking of the corner as the center of the quarter-circle.
I did it just by observation. That the ratio is about 0.5 .Now 39=3x13. And 13²=12²+5². A Pythagorean triplet. And picked it up.