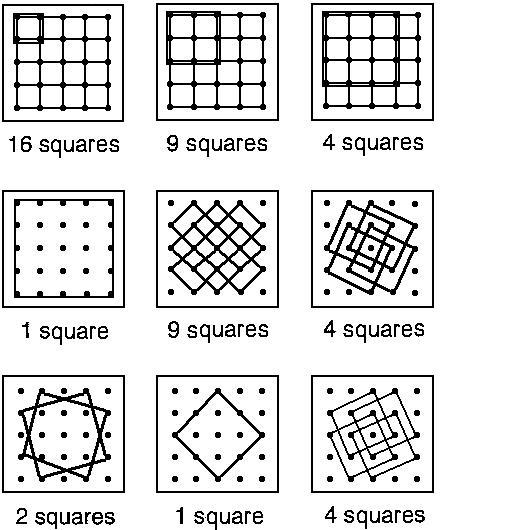
Squares in the grid
How many squares can you make using points on this 5 × 5 grid as their vertices?
Three possible squares are shown.
Note : Some of the squares can be the same size, and they can overlap one another.
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
 If we add all the numbers
1
6
+
9
+
4
+
1
+
9
+
4
+
2
+
1
+
4
=
5
0
squares.
If we add all the numbers
1
6
+
9
+
4
+
1
+
9
+
4
+
2
+
1
+
4
=
5
0
squares.
Moderator note:
If you're not someone who normally checks our Advanced problems and happen to be up for a challenge, the triangle variant of this problem is here:
By area these are 1, 4, 9, 16, 2, 5, 10, 8, 5 The ones with area 5 are all congruent, just turned opposite ways, as are the two with area 10.
Log in to reply
No need for area here.
Log in to reply
I just thought I'd share since that's how I categorized them.
Log in to reply
@Jeremy Galvagni – Nice idea, l just thought l solved it the easier way by counting :)
I also used the same Technique. :)
Log in to reply
I also used the same Technique. :).:)
Why not 25 combination 4 ??? 25 being the number of dots, choosing 4 dots (there are 4 vertices of a square) would give us the possible combination of using all those dots (4 at a time ) together.
Log in to reply
If you want this method, there is more to it. We can approach this problem using combination.
Log in to reply
Please do! That would be much more illuminating!
Log in to reply
@Joshua Nesseth – I wrote my solution. I am not writing another one :)
Yup but that will also consider 4 collinear points or any other 4 points that doesnt make a square
I didn't know that you could rotate the squares in any way, I'm an idiot.
Log in to reply
Especially since examples of rotation in two different sizes and orientations are shown in the diagram.
Gosh! Made a stupid count mistake at the first square type.
Is there a formula to find such squares from any arbitrary no. of points or is it just visualization???
Log in to reply
The solutions provided below indicate formulas, even in the comments too. I was lazy at the beginning to use any formulas. The first thing that came to my mind is counting the squares.
General solution for a p × q grid, with p ≤ q . A coordinate system can be defined with 1 ≤ x ≤ p and 1 ≤ y ≤ q .
For any square S , consider the minimum and maximum coordinates of the vertices, x min , x max , y min , y min . It is not difficult to see that d : = x max − x min = y max − y min > 0 . Define x ⋆ such that ( x ⋆ , y min ) is a vertex of the square; if there are two such vertices, choose x ⋆ as large as possible. Any valid square is now fully specified by
-
1 ≤ d ≤ p − 1 ;
-
x min + 1 ≤ x ⋆ ≤ x min + d ( d possible choices);
-
1 ≤ x min ≤ p − d ( p − d possible choices);
-
1 ≤ y min ≤ q − d ( q − d possible choices).
Therefore the number of squares is N p , q = d = 1 ∑ p − 1 d ( p − d ) ( q − d ) = d = 1 ∑ p − 1 ( d 3 − ( p + q ) d 2 + p q d ) = 4 1 p 2 ( p − 1 ) 2 − 6 1 ( p + q ) ( p − 1 ) p ( 2 p − 1 ) + 2 1 q p 2 ( p − 1 ) = 1 2 ( p − 1 ) p ( p + 1 ) ( 2 q − p ) . In this case, p = q = 5 so that we find N 5 , 5 = 1 2 4 ⋅ 5 ⋅ 6 ⋅ 5 = 5 0 .
Before solving the problem, I saw you wrote a solution and I knew you had a general formula! I tried to do derive it myself, but ultimately I just counted them all. This is a beautiful solution. I really like how you managed to specify each valid square, especially how you "limited" square by x m i n and y m i n and brought in x ⋆ , that's what I didn't know how to do. I admire your thinking and creativity!
One small thing though: regarding listing how any valid square is fully specified, doesn't it seem "more logical" to first specify x m i n and y m i n and only then x ⋆ ? Here's how I understood it:
1) You choose d .
2) You choose x m i n and y m i n .
3) You choose
x
⋆
, which must be on line
y
=
y
m
i
n
and determines the square (as shown in the figure).
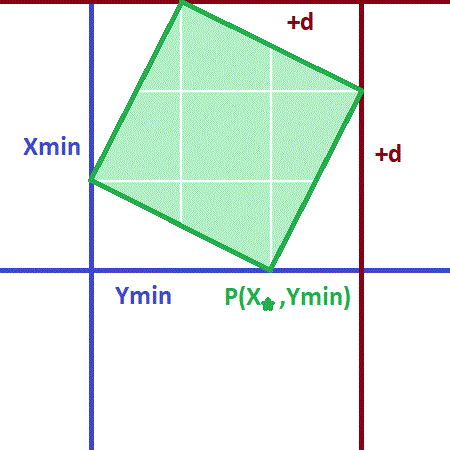 Values for
d
,
x
m
i
n
,
y
m
i
n
and
x
⋆
on the image are taken randomly.
Values for
d
,
x
m
i
n
,
y
m
i
n
and
x
⋆
on the image are taken randomly.
Log in to reply
Yes, that works fine. I used x max and y max only to show how I defined d .
By the way, Uros, thanks for posting the picture that I was too lazy to make :D
Log in to reply
Thanks, it was my pleasure! :D
If you want, check out my latest problem Archer duel , solution to it is partially inspired by this solution.
I am a high school student , and i can never derive a formula like this , i just wanted to know that have you ever done questions similar to this or its a new question for you.
Log in to reply
This one was new to me. However, I have done many "counting" problems before. The trick is to find a relatively simple set of numbers that describe the objects you study, and work out the appropriate sums.
I thought of binomial coefficient at first because im still in high school i tried to solve with dots first then tried horizontal and vertical lines and it didnt work in both cases
I am SO going to be able to see the math in the world as you do! Thank you for the motivation!
Can anyone please explain the part After d³-(p+q)d²+pqd
Shouldn't it be d²(d+1)² - (p+q) {d/6 (d+1) (2d+1)} + pqd(d+1)/2
Log in to reply
Consider sums k = 1 ∑ n k 3 , k = 1 ∑ n k 2 and k = 1 ∑ n k .
If the sum were from d = 1 to d, then your expression would be correct. However, the sum is from d = 1 to p - 1, so substitute d : = p − 1 in your result.
Each square takes up the same horizontal and vertical length, even if the square is tilted.
There are 4 × 4 = 1 6 spaces that are 1 × 1 , with only one possible type of square that can fit in this space.
In general, an n × n space has n different squares that fully occupy that space, as all the n first points on the top row can be chosen as the starting point, and each successive point is going to be the same distance in from the corner on the next face going clockwise, and starting from the rightmost point is equivalent to starting from the leftmost.
So, we have 4 × 4 × 1 + 3 × 3 × 2 + 2 × 2 × 3 + 1 × 1 × 4 = 5 0 distinct squares.
This is how I solved it. Also I'm pretty sure you meant squares instead of "suarea".
This is a neat approach. Can you add a diagram?
Although there is way too much stuff contained in "Thus..." I love it. So elegant!
Can you please elaborate your answer?
please explain more wide..!!
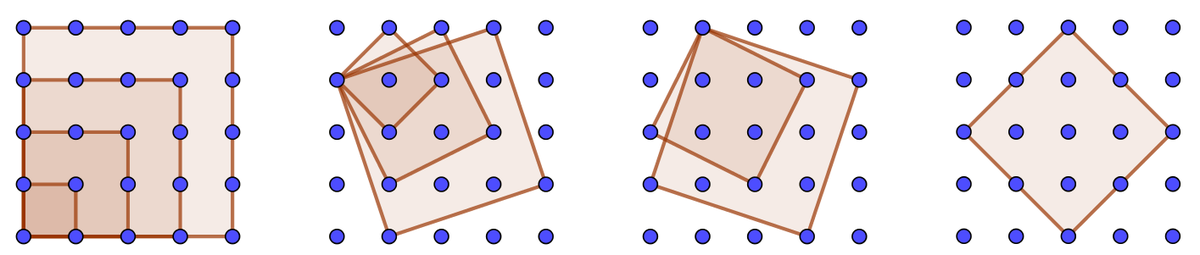 My strategy was to consider side leght/orientation combinations from vector forming the sides. In the first figure, the vectors are (1,0), (2,0), (3,0), (4,0). In the second, (1,1), (1,2), (1,3) ((1,4) is not possible). In the third, the reflections of (1,2) and (1,3). Finally in the fourth, (2,2), which is the largest without leaving the grid.
Now you just have to count how many translations each square can have. Grouping by figure, we have
(
1
6
+
9
+
4
+
1
)
+
(
9
+
4
+
1
)
+
(
4
+
1
)
+
(
1
)
=
5
0
.
My strategy was to consider side leght/orientation combinations from vector forming the sides. In the first figure, the vectors are (1,0), (2,0), (3,0), (4,0). In the second, (1,1), (1,2), (1,3) ((1,4) is not possible). In the third, the reflections of (1,2) and (1,3). Finally in the fourth, (2,2), which is the largest without leaving the grid.
Now you just have to count how many translations each square can have. Grouping by figure, we have
(
1
6
+
9
+
4
+
1
)
+
(
9
+
4
+
1
)
+
(
4
+
1
)
+
(
1
)
=
5
0
.
(4^2 + 3^2 + 2^2 + 1^2) + (3^2 + 2^2 + 1^2) + (2^2 + 1^2) + 1^2 = 50 Brackets contain different orientations.
To make a square select any 2 dots from 25 dots of the grid =25C2
The other two dots are automatically arranged so as to form a square .
But all the squares counted are repeated
5
C
2
times.
Therefore the required answer=
25C2/4C2 = 50
For a general n×n grid the number of such squares = (n×n)C2 / 4C2
I counted the small squares in the puzzle then multiplied it by the number of dots on one side and got the answer
16 x 5 = 50?
formula might be
(n-1)(n-1)+(2)(n-2)(n-2)+3(n-3)(n-3)+4(n-4)(n-4)......till it becomes zero
1 2 × 4 + 2 2 × 3 + 3 2 × 2 + 4 2 × 1
it is 50 bc i said it was 50 so here's the answer have a nice day