Stacking Blocks Fun
You want to stack blocks, as shown, in such a way that they don't fall and the overhang H ( n ) is maximized. Each block has the same length l = 1 m .
To 2 decimal places, evaluate n → ∞ lim ln ( n ) H ( n ) , where ln ( ⋅ ) is the natural logarithm.
Note: Let M be the positive integer for which the equilibrium is unstable, no matter the position of the blocks. Then H M = H M + 1 = ⋯ = 0 .
The answer is 0.50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The limit as n − > ∞ of
I n ( n ) I n ( n ) + γ
is 1 , not γ
Maybe ask for the limit of H ( n ) − 1 − I n ( n ) ? Then the correct answer would be γ .
Log in to reply
But the limit is 2 l , which is 0 . 5 , not γ .
Log in to reply
In fact, k = 1 ∑ n k + 1 1 = H ( n ) − 1 , where H ( n ) is the Harmonic Function. The limit as n − > ∞ of H ( n ) − 1 − L o g ( n ) is γ − 1 . On the other hand, the limit of the ratio L o g ( n ) H ( n ) − 1 is 1 .
Log in to reply
@Michael Mendrin – Perfect (so there is no problem right?). That expression has to be multiplied by half the length of a block in order to obtain the physical overhang fron the table of the pile of blocks.
Log in to reply
@Gabriele Manganelli – Wait a minute, is the correct answer 0 . 5 or 0 . 5 7 7 . . . ? But, yes, if L = 2 1 , then the ratio becomes 0 . 5 .
Log in to reply
@Michael Mendrin – The correct answer is 0 . 5 0 .
Log in to reply
@Gabriele Manganelli – well, check the wording of the bottom of your solution
Log in to reply
@Michael Mendrin – Sorry for the misleading way I wrote it before, thank you for your time
Log in to reply
@Gabriele Manganelli – I actually liked the way γ came up with this problem, but oh well.
This problem of building an overhanging tower of blocks is an old one, but it still boggles my mind, that it could overhang without limit.
Let 2 L be the length of a block and m its mass.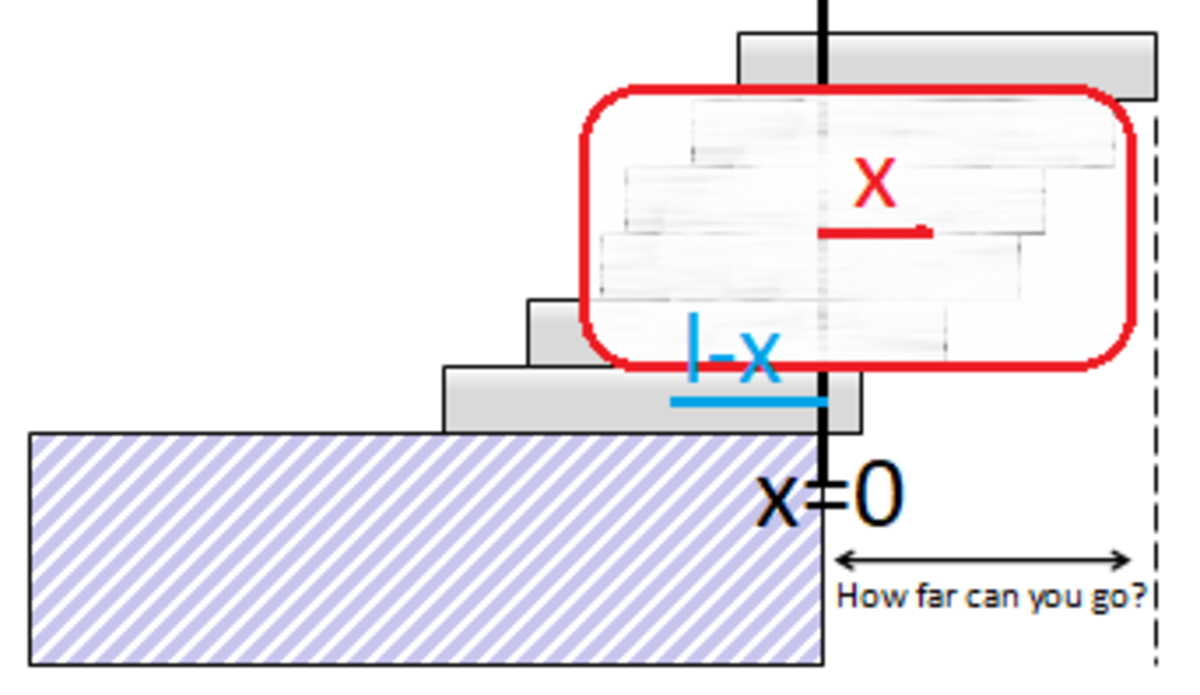
Consider the situation showed: a pile of
N
+
1
blocks can be thought as a pile of
N
above one, with center of mass displaced
x
from the border of the table, which we will choose as origin.
In the case of maximum overhang,
x
is also the position of the edge of the bottom block, whose center of mass is in
−
(
L
−
x
)
.
To achieve equilibrium the center of mass of the system should be in the position
x
=
0
, which gives
m
⋅
(
N
+
1
)
m
⋅
(
N
x
−
(
L
−
x
)
)
=
0
resulting in
x
=
N
+
1
L
.
The situation of the problem can't be solved exactly like this, however we can imagine repeating this reasonment for each block starting from the higher one, finding a relative displacement between the center of mass of two consecutive blocks of x = N + 1 L .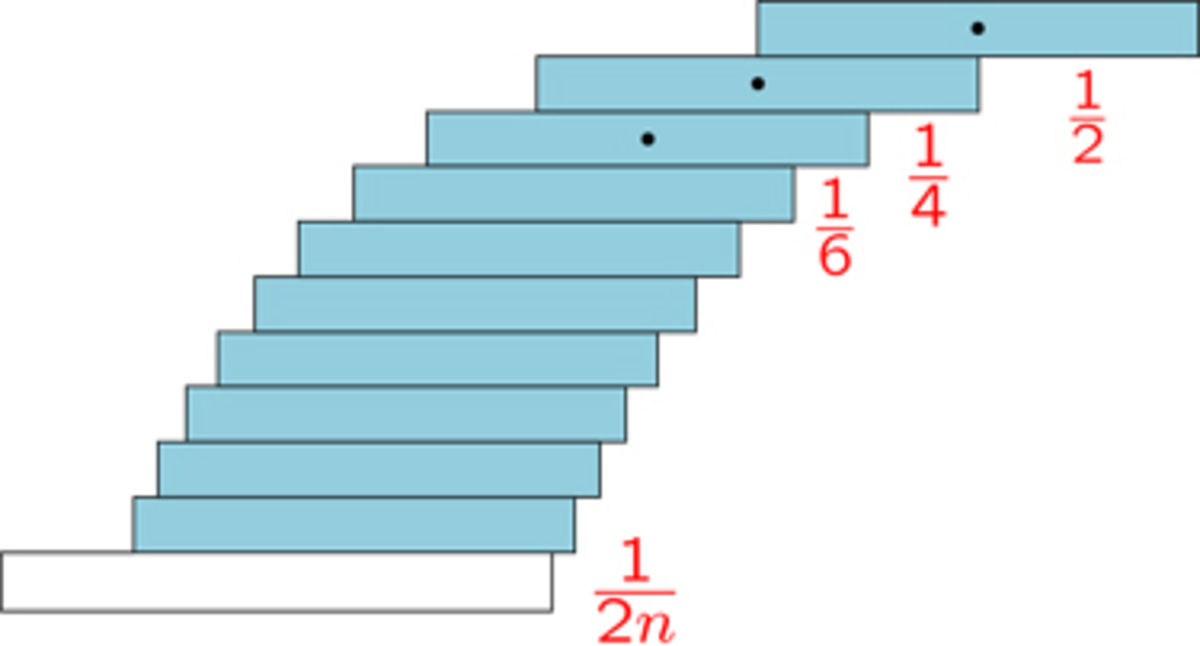
Here you can check that for example the "big block" equivalent to the higher two has a center of mass which is displaced by
L
from the one of the third block.
The overhang is therefore H ( N ) = L ⋅ 1 ∑ N k + 1 1 , the armonic series, which tends to L ⋅ ( l n ( N ) + γ ) as N tends to infinity. Plugging L = 2 1 leads to the answer 0 . 5 0 0 .
Curiosity: γ ≃ 0 . 5 7 7 … is known as Euler-Mascheroni constant .