Stacking Right Triangles

Geometry Level 2

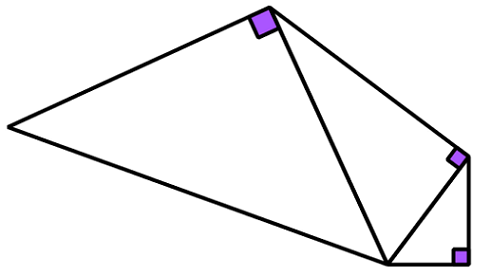
The above diagram shows three right triangles, each with all integer lengths being stacked on one another.

If the length of the smallest side of the smallest triangle is 3,
what is the length of the largest side of the largest triangle?

Note : Diagram not drawn up to scale.

The answer is 85.

1 solution

Samara Simha Reddy
Apr 25, 2016

Relevant wiki: Pythagorean Triples

$\large \displaystyle \text{ The formula used for the above triangles are, } a^2 + b^2 = c^2. \\ \large \displaystyle \text{Where all the sides of the triangle are integers}.\\ \large \displaystyle \implies 3^2 + 4^2 = 5^2, 5^2 + 12^2 = 13^2, 13^2 + 84^2 = 85^2.\\ \large \displaystyle \therefore \text{The largest side is } \color{#D61F06}{\boxed{85}}.$

Pythagoras Theorem is used. Where sum of squares of the numbers forms another square number, which is possible only with one integer

how do you get 84 to be b in $13^2$ + $84^2$ = $85^2$ .

Ayush G Rai - 5 years, 1 month ago

You know that one of the side of the biggest triangle is 13, and you also know that the triangle must be rectangle. So let's say that the ipotenuse is x and the other side is y. For the pythagorean theorem you have: $x^2=y^2+169$ . But this is equivalent to say: $x^2-y^2=169$ or $(x+y)(x-y)=169$ . Since x and y are integers you can solve a simple sistem of linear equations: $x+y=169$ and $x-y=1$ (You can easily find out why I didn't say y-x=1 or why the system isn't x+y=13 and x-y=13, or other combinations of values...). So the solutions are $x=85$ and $y=84$ !

Luca Ferrigno - 5 years, 1 month ago

very good answer....+1

Ayush G Rai - 5 years ago

Using calculator :D

Samara Simha Reddy - 5 years, 1 month ago

that is too simple????

Ayush G Rai - 5 years, 1 month ago

@Ayush G Rai – Nope. It took a while for me to find out. $\large \displaystyle \ddot\smile$ .

Samara Simha Reddy - 5 years, 1 month ago

Why $85$ WHYYYY ( I stuck in the biggest triangle )

Jason Chrysoprase - 5 years, 1 month ago

Hmmm, can you explain why 85 must be the minimum value? Or in other words, why can't the answer be smaller than 85?

Chung Kevin - 5 years, 1 month ago

You won't get other integer combined with a integer which is a perfect square.

Samara Simha Reddy - 5 years, 1 month ago

And how did you know that?

Chung Kevin - 5 years, 1 month ago

@Chung Kevin – Work out :)

Samara Simha Reddy - 5 years, 1 month ago

Stacking Right Triangles

The answer is 85.

1 solution

0 pending reports