Standard wedge - block problem.
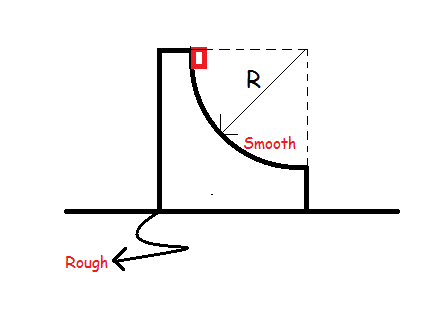 Consider a wedge of mass
m
whose upper surface is a quarter circle and is smooth. The lower part is rough. A small block of same mass is kept at the topmost position and the initial position is shown in figure. The block slides down the wedge.
Consider a wedge of mass
m
whose upper surface is a quarter circle and is smooth. The lower part is rough. A small block of same mass is kept at the topmost position and the initial position is shown in figure. The block slides down the wedge.
Find the minimum value of coefficient of friction between floor and lower surface of wedge so that the wedge remains stationery during the block's motion on it.
Details and assumptions
- Assume that block and wedge don't topple.
- The given information is complete. Nothing else is needed.
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Just wanted to thank you Jatin for the hint you gave in your previous problem. I couldn't have done your problem without it :)
Can anyone tell me how to upload a diagram????....the solution can be understood well
Log in to reply
Hi,
First, there is a mistake. Never say f = μ N 1 . You should have said that f ≤ μ N 1 , and hence, μ ≥ N 1 f . You should have said that f = F h , where F h = 3 m g sin θ cos θ is the horizontal force on the wedge.Then μ ≥ 1 + 3 sin 2 θ 3 m g sin θ cos θ . This will be satisfied for all values for theta. Hence, μ is greater than or equal to max value of RHS which is 0 . 7 5 .
On image posting:
First get a url for the image and then type:

Log in to reply
Yes....you are right...i should have written it like that.....Thanks!
OK boss! :D
Log in to reply
@Tunk-Fey Ariawan – Ha ha!
This was one of the first things told by my teacher that you should never have a habit of writing f = μ N
Log in to reply
@Jatin Yadav – In my opinion, it should be
f s ≤ μ s N and f k = μ k N .
Log in to reply
@Tunk-Fey Ariawan – Yes, you are right! We generally mean μ s by μ
@Jatin Yadav – In eq 4, shouldn't we add the force due to the weight of the small block?
In eq 4, shouldn't we add the force due to the weight of the small block?
can you please post the pic of FBD diagram
Very stupid @Brilliant member if u are truly a brilliant member He has considered them different objects and not a complete system .. He has taken normal of that mass m ...
easy question
Let the angle which the block makes with the horizontal while sliding down the wedge at any instant be θ
Let the block's velocity be 'v'
Using Energy Conservation
2 1 m v 2 = m g R sin θ . . ( 1 )
Also..as the block is in circular motion
N − m g sin θ = R m v 2 . . ( 2 )
where N is Normal Force exerted by the wedge on the block
On solving the above to equations..we get
N = 3 m g sin θ
Now..from the FBD of the wedge we get
f = N cos θ = μ N 1 . . ( 3 )
where N 1 is normal force on wedge by the ground
Again from the FBD of wedge..we get
N 1 = N sin θ + m g . . . . ( 4 )
Substituting the value of N 1 in eqn 3
μ = m g + N sin θ N cos θ
Now putting N = 3 m g sin θ
we get μ = 1 + 3 ( sin θ ) 2 2 3 sin 2 θ .. 5
To minimize μ . . . . d θ d μ = 0
⇒ 3 cos 2 θ ( 1 + 3 ( sin θ ) 2 ) − ( 2 3 sin 2 θ ) ( 3 sin 2 θ ) = 0
Now putting cos 2 θ = 1 − 2 ( sin θ ) 2 and sin 2 θ = 2 sin θ cos θ
we get
sin θ = 5 1
Substituting s i n θ in eqn 5
we get
μ = 0 . 7 5