Star Rock It
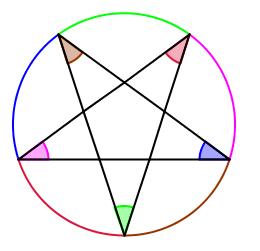 Find the sum of the angles (in degrees) in a pentagram.
Find the sum of the angles (in degrees) in a pentagram.
Do you know the general formula for an n -polygonal star?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
42 solutions
A pentagon has 5 sides, can be made from three triangles, its interior angles add up to 3 × 180° = 540° for pentagon (all angles the same), then each angle is 540° / 5 = 108° (three interior angles 36+36+36)
FOR ANY POLYGON : Sum of Interior Angles = (n-2) × 180° Each Angle (of a Regular Polygon) = (n-2) × 180° / n
Log in to reply
This is a PENTAGRAM, not a PENTAGON.
Log in to reply
That is a pentagram consisting a pentagon.
Log in to reply
@Mukul Mishra – I know, but the solution I replied on needs to be amended. It isn't complete.
@Yohan Gadde Sorry for writing the words in caps. I used caps to stress on those words, and I can't italicise or underline the words because I don't know LaTeX. My apologies for sounding rude in my previous comment.
how come you divided 108 into 3 equal parts. is there a rule stating that in a pentagram that the interior angle will be divided into 3 to get the angle of one of the spikes of the star?
I can't read, it says pentagram, not pentagon.
180degree angle subtended at circumference is half at center..
ভাইরা যা লিখেন বুজিয়ে লিখবেন...
by using incribed angle theorem we have to solve this if we ad all the angles we get 1/2 * measure of circle that is 180
I didnt understood the solution. Can you elaborate it pls?
oh i get it... it is because its just an inscribe angle, so it is must divided into two.
what's the difference between pentagon and pentagram?
The pentagon is the central figure and the sum of its 5 angles would be 360 degrees
Log in to reply
Hi see the response
for Pentagon
No of sides= 5
Sum of Interior Angles= 540°
Each Angle = 108°
540 is the correct ans. a pentagon has 5 obtuse angles, therefore must be more than more than 180. see Yohan Gadde ans.
Log in to reply
This is a PENTAGRAM, not a PENTAGON.
Log in to reply
in response to aniruddha bhattacharjee .i agree with your point that it is a pentagram, not a pentagon............pentagon is type of regular polygon and the each internal angle is 36 degree in a pentragram .so, the correct answer is 180
They are discussing the pentagon at the center of the pentagram.
we have that 180n -720 let n is the no of sides in a star
star has one 5 point and one point = 36 degree and total sum of star 36+36+36+36+36
yes 540 108+108+108+108+108=540
Oh!I like the equation.I got it easily.T.Y.
arc length from one point to another is 360/5 = 72 deg. the central angle in relation to the two sides of the star is therefore 72 degrees. the colored angle therefor is 72/2 (from the properties of inscribed angles. so each colored angle s 36 degrees. the sum theresfore is 36*5 which is 180.
great answer
When you initially look at the pentagon in the center, you can calculate the sum of the interior angles as 540. (number of sides - 2) * 180 = 540. Therefore each interior angle is 108 (540 / 5 = 108). By extending the lines of the pentagon sides to form chords, we can calculate the complementary angle of each line (chord) as 72 degrees. Since the chords intersect, we can show that the chords and the pentagon form an isosceles triangle. By definition of an isosceles triangle, the two interior angles are equal. Again, using the formula to calculate the sum of the interior angles of the isosceles triangle, we note that the sum of the interior angles is 180. We now can calculate the 3rd angle as x=180-2(72), or 36. Since there are 5 triangles, we can calculate the total sum of the angles of the pentagram as 36 * 5 (number of points) = 180 total degrees.
I don't have any good explanation but this is what I did: Just see the angles- they are less than 90 degree and some where around 45. So sum total being 90 degree would be out of question because then each angle would be 18 degree. And it cannot be 360 degree as each angle will give 72 degree. But it can be 180 degree which will make each angle to be 36 degree. Just my theory.
the sum of angle is 180 in level 1
36 +36 +36 +36 +36 = 180 degree
how it is 36??/
Log in to reply
Every interior angle of the pentagon = 108 degrees Two equal angles inside each triangle = 180-108=72 degrees One of the angles to find = 180-(2x72) = 36 degrees
the internal angle of a pentagram is 36 degree
Each angle of the pentagon of middle ar equal & they are 108. then, each angle of the pentagram can be found by the equation came from triangle , 180-(180-108)-(180-108). then multiplying the product by 5 we can get the ans.
The sum of all angles in a pentagon is 540 degrees. Given the pentagon here is equilateral, each of its angles are 108 degrees (540/5=108). We can then determine that the supplemental angle of any of the star's five longest line segments is 72 degrees (180-108=72). Given that the triangles are all isosceles triangles, we can determine that both angles closest to the pentagon are 72 degrees, leaving the other one to be 36 (180=72+72+36). 36×5 is 180 degrees, and there's your solution.
SIMPLY
USE
EXTERIOR ANGLE THEOREM
the inner pentagon angles sum is 540 and each angle is 540÷5=108, from the straight lines each complementary angle=180-108=72 so the highlighted angel is 36, so the angles sum is 36*5=180
Sum of all angles of any n-polygram is always \180 degree\ where, n is always a odd natural number, although sum of all angles doesn't depend on no. of sides (spikes).
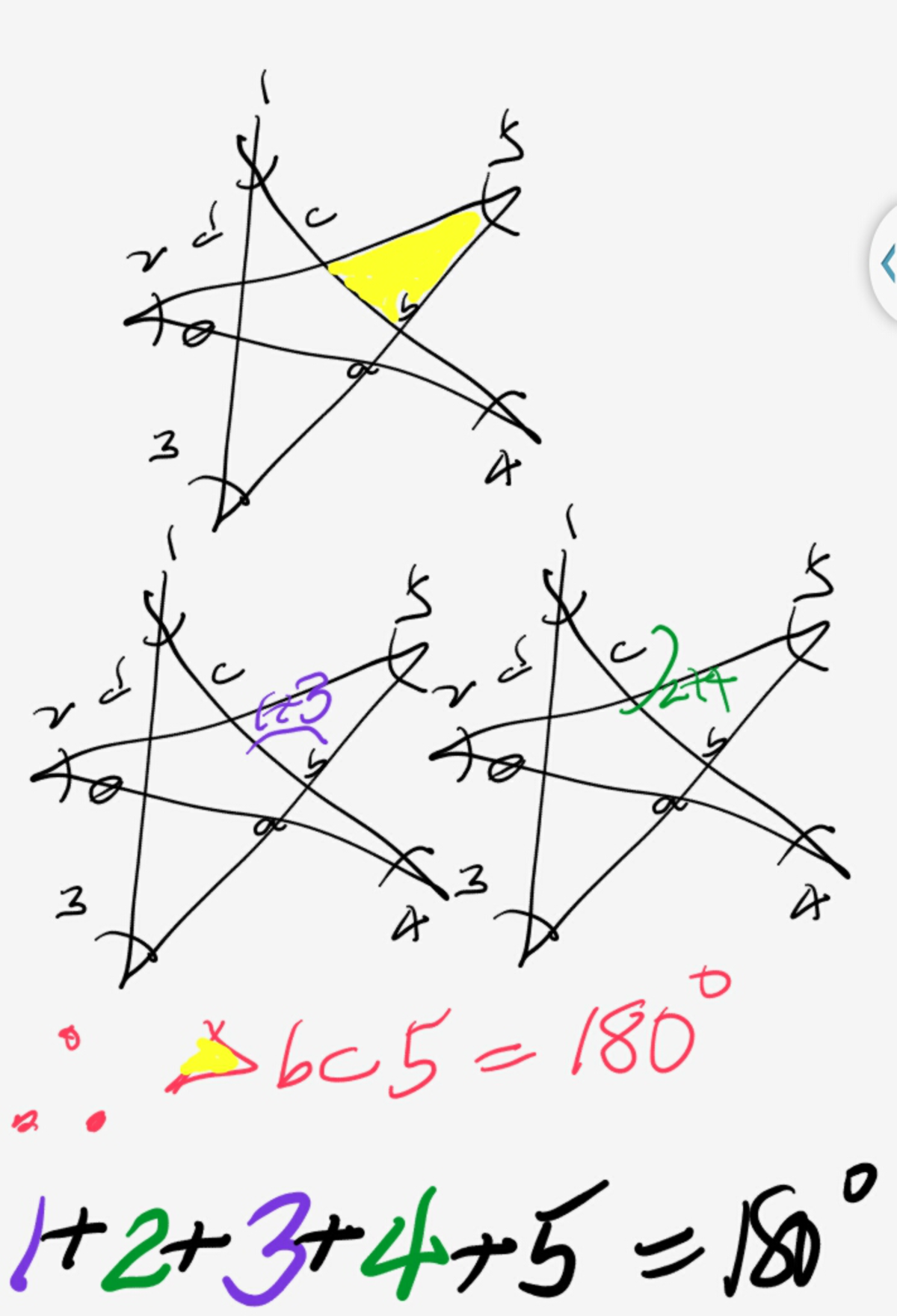
- sum of angles in a triangle = 180
- supplementary angles add up to 180
This is a star under circle since star has 36 for its each angle i.e, total 180
A pentagram is a five-pointed star (go Google it). For me, I solve this QN via a longer method. In the star, I found that there are 5 triangles (with overlap) and adding them together 180°×5 which include 2× of the sum of the coloured angles and the interior angles of the pentagon (180°×3). So u will get (180°×5-180°×3)/2=180°
The angles adjacent to the interior of the polygons measure 72 degrees, because the interior angles of a regular pentagon is 108 degrees. Therefore, the measure of the interior angle is equal to 36 degrees. Since there 5 angles, the angle sum of the five interior angles, r the angle sum of a pentagram is 180 degrees.
los 5 angulos suman 180ª por propiedad
In the Pentagram, a Pentagon is created. The measure of every angle in a regular pentagon is 108°.
Now consider one of the triangles whose base is a side of the Pentagon. Two of its angles form a linear pair with the Pentagon's angles. Thus, both angles are equal to 180° - 72°= 108°.
Therefore, the value of one of the angles is equal to 180° - (Sum of the other two angles)
= 180° - (72° + 72°) = 36°
Thus the sum of all the shaded angles is equal to 5 (36°) = 180°.
I did it a little bit of a convoluted way. First, find the internal angles of the central pentagon (180 3/5=108). Next, as the angles on a straight line add up to 180, find the angle of the equivalent corners inside the "points" (180-108=72). To find the point angle, use the rules for isoceles triangles to get a result of (180-(72 2)=36) for the point. Times this by 5 to get 180, and the sum of angles in a pentagram.
Within the pentagram is a regular pentagon, which according to the formula (n-2)×180
(5-2)×180=540°
Each interior angle of the pentagon is 540°÷5=108°
The triangles that connect to the pentagon to form the star of the pentagram are isoceles triangles, so by default two angles will be equal.
The internal angle of one of the triangles is (72+72+36). 72° is found because the line connecting the pentagon to the triangle is a straight line and therefore 180° (180-108=72)
As out of the three angles, thereis one different angle, that is the angle which has been highlighted. Multiply the angle (36°) by 5, which is the number of angles highlighted, and you get the answer, 180° 36°×5=180°
So, I agree with the formula solutions I have seen (180(n-4) or 180n-720), but the sum of the internal angles for polygonal stars depends on how they are drawn. For example, if you draw a 8-pointed star polygon by connecting every other point, the sum of the internal angles will be higher than if you connect every 3rd point. Does anyone have a formula that accounts for this? (I think I do.)
Please see a pentagon at the centre. Each angle will be 540/5 =108 since all sides are equal Now go to each triangle and see the base angles as 180-108 =72. Now one of the vertex angle is 180 - 72*2 = 36
Now answer Sum = 36*5 = 180 because of symmetry.
in pentagon every angle is 108 dividing by 3 we get 36 now the star have 5 edges so 5 * 36 = 180
For such star shaped figures, total sum = 180(N-4) . here N=5
The general formula of determining the sum of the angles in a n-polygonal star is = 180(n-4) degrees . Here n=5 so the answer is = 180 degrees. Also , the general formula of determining the value of each angle of a n-polygonal star is = 180(n-4)/n . Using this formula, we can get the value of each angle of a pentagram is 36 degrees.
this is one of those clutch theorems to have in your back pocket ... the angle is half the arc it creates inside a circle - so here we have 360 degrees (the colored arcs are a circle) and the angles making that up measure half that i.e. 180 degrees (and each of those measure 36 degrees)
shape formed by the star in the middle is pentagon so each angle of pentagon is 108 and it forms isosceles triangle with two points of star, so 2x+108=180=) x=36 so, 5*x=180
Each of the colored angles is an inscribed angle since their vertices lie on the circle. The relationship between an inscribed angle and its intercepted arc is given by the equation:
Arc = Angle * 2 or Angle = Arc * (1/2)
Since all the arcs in a circle add up to 360 degrees and we are assuming each of the intercepted arcs formed are congruent, each arc has a measure of 72 degrees by:
360/5 = 72
Since the arc has a measure of 72 degrees and the inscribed angle must be half the measure of its intercepted arc, each of the angles must be 36 degrees.
Since we have 5 angles, each of which has a measure of 36 degrees, we get:
36 * 5 = 180 degrees
pentagon, can be made from three triangles, its interior angles add up to 3 × 180° = 540° for pentagon (all angles the same), then each angle is 540° / 5 = 108° (three interior angles 36+36+36)...this symmetric star divides each big angle of pentagon equally into 3 then angle 36...................then 36*5=180
Instead of doing something so complicated, we can see that the bases of all the triangles on the outside of the inscribed pentagon are congruent, showing that the pentagon is regular. Now, we can see that a pentagon has 540 degrees, and 540/5 because of each angle gives a measure of 108 degrees for each measure. Using supplementary angles, we see that the angles on the base of each triangle is 72 degrees. 180- (72 2) gives 36 degrees for each marked angle measure, and 36 5 gives a sum of 180 degrees, which is our answer.
Each angle is 36 so 36×5=180.
Due to the way the star is constructed, the pentagon at the centre is clearly regular. If you know that the interior angles of the pentagon are all 108 degrees then the angles in the triangles of the star (excluding the highlighted ones we need to find) are all 72 degrees (as on a straight line). We can then find out the size of each highlighted angle (180-2x72), which is 36 degrees. As all the highlighted angles are the same size- the sum of the angles is 5x36 degrees, which is 180 degrees.
In general the sum of the angles (at the ends of the star) is (n-4)*180 for when n is greater than or equal to 5 and 'n' is the number of points of the star. If n=4,n=3 the formula doesn't work because you cannot construct a star from a 'base shape' in this way if 'n' is less than 5 as you either get impossible shapes, perpendicular edges (which can't draw stars) or a triangle (which is just 180 degrees).
I hope that made sense.
nice you Imagine star
I did this by using an inscibed angle off its central angle. Since there are five equal inscribed angles there are five equal central angles. 360 degrees divided by 5 is 72 degrees. Each inscribed angles is 1/2 of its central angle = 36. Now times that by 5 and you get 180 degrees.
Each interior angle = 108 which is equal to 108/3 = 36 degrees therefore each angle = 36 degree there are 5 five such angles in the given pentagram 5 angles*36 degrees = 180 degrees
We see that an entire circle is inscribed by n angles (the value of n doesn't matter). In a circle, the measure of inscribed angles is exactly half the measure of the arc inscribed. Thus, we have 360 degrees / 2 = 180 degrees.
easiest way is to imagine about a regular pentagram. just use angle sum property to find angle at one end of the star and multiply it by five
we just have to use the exterior angle property in any of the small triangles and then the angle sum property
We know that sum of all the internal angles in a quadrilateral is \rightarrow \quad \quad 180*(n-2) Therefore for a pentagon, Sum of all the internal angles =180(5-2)=180(3)=540 Now it is a regular pentagon . Therefore Each angle is equal. Let each angle be x. Therefore, 5x=540. Therefore x=108. Now observe any triangle among the five triangles whose vertical angle is included in the sum to be found. We can easily observe that the both the base angles of the triangles are in linear pair with internal angles of pentagon. So we can easily find the both the base angles to be equal to { 72 } Now as all the three angles of triangle equal to 180 degrees ,we can easily find the third angle to be equal to 36 degrees. Similiarly we can find all the three angles and finally add them as 36+36+36+36+36=180
->The inside part of the star can be seen as a regular pentagon. ->Each angle = {(5-2) 180}/5 =108 ->Now,there are 2 straight lines as we can see formed to be a triangle after the pentagon. ->The triangle is an isosceles triangle as the star is formed equally. -> So, the inside angles of the triangle ={ (180-108) 2 }+ x = 180 ->So, x = 36 .
Simple :D
The angle of a chord on the circumference is half of the angle by same at the center. Looking at the diagram all chords sum up 360 at center so the sum at circumference ie the sum of angles of the star is 180