Starting with a rectangular board

Probability Level 4

Integers $x$ and $y$ are each independently chosen uniformly and at random on the interval from $1$ to $8$ .

Then two players start with an $x \times y$ grid of squares.

They play a game where each player takes turns removing an $n \times n$ square, $1 \leq n$ . The person to remove the last square loses the game.

For example, a $5 \times 3$ game might be played as follows:

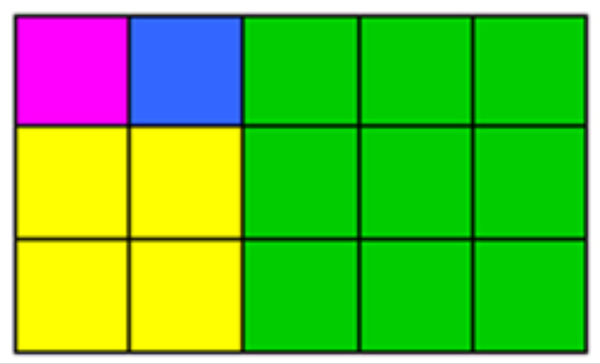
Player one takes the $3 \times 3$ green square.

Player two takes magenta.

Player one takes yellow.

Player two takes blue. (and loses)

For how many of the $64$ possible starting boards does the player who goes first have a winning strategy?

Inspiration : Conversation with @Henry U

This is a follow-up to this problem.

The answer is 53.

1 solution

Geoff Pilling
Jan 5, 2019

For an $n \times 1$ board it is straightforward to see that the second player wins for odd $n$ . This includes 7 boards.

The second player can also win for a $4 \times 2$ or a $5 \times 2$ board. This is an additional 4 boards.

This is a total of 11 boards so far...

For all other boards (53 possibilities) the player who goes first can force a win.

The matrix below shows the strategies for each case... (Thanks to @Henry U for helping me get this started)

A is a win for the first player. B is a win for the second player.

Subscripts indicate strategies. The position in the array corresponds to the dimensions of the original board.

T = Trivial win. No strategies needed.
S = Take square of side length n-1
L = Take large square leaving a 1 by x rectangle with an odd number of squares
M = Take a square surrounded by a single row of squares on three sides
<n> = Take an nxn off the end leaving the next player with a losing position
C = Split the playing field into two identical chunks each of which contains at least one 2x2 following move for move what the other player does but in the opposite chunk until one chunk only has unit block blocks left for the taking at which point you remove all but an odd number of unit blocks (note it is ok to leave a few extra unit blocks laying around as they are harmless, and any time he grabs one you grab one and proceed with the game
D = This is a tricky one. Start with the central 2x2. Then do a "tit for tat" strategy except for the first move which needs to be in the middle of the first row/column of 3. After that, with the right moves you can guarantee that an odd number of 2x2's are taken, not including the one you took on your first move. This is the best I can describe short of going into every possible permutation of moves. Thanks to @David Vreken who helped me realize the subtleties of this particular case.
W = If the first player takes a 2x2 you take a single square and vice versa
V = Same strategy as W unless he goes in one of the two middle spaces in which case you grab the other one and then proceed as in W

$\begin{array}{cccccccccccc} &1&2&3&4&5&6&7&8 \\ 1&B_T&A_T&B_T&A_T&B_T&A_T&B_T&A_T \\ 2&A_T&A_S&A_M&B_W&B_V&A_2&A_2&A_C&&& \\ 3&B_T&A_M&A_S&A_L&A_C&A_C&A_C&A_C&&& \\ 4&A_T&B_W&A_L&A_S&A_M&A_4&A_C&A_D&&& \\ 5&B_T&B_V& A_C&A_M&A_S&A_L&A_5&A_C&&& \\ 6&A_T&A_2&A_C &A_4&A_L&A_S&A_M&A_C& \\ 7&B_T&A_2&A_C & A_C &A_5&A_M&A_S&A_L&&& \\ 8&A_T&A_C&A_C& A_D& A_C& A_C&A_L&A_S \\ \end{array}$

Can you go over the strategies for an $8 \times 4$ grid? I am interpreting your instructions for $A_C$ that A begins by placing a $4 \times 4$ square in the center to split the field into two identical chunks. But if A does that, then B can respond by placing a $2 \times 2$ square in the vertical center on one side, and guaranteeing a win by making sure that the end board has an even number of $2 \times 2$ squares.

(I still had the $8 \times 4$ grid as a win for A, but with a different strategy that was a little more complex.)

David Vreken - 2 years, 5 months ago

Whoa... Looks like you are right? I'll need to take a closer look... Lemme guess... Does your strategy involve A starting with the central 2x2?

Geoff Pilling - 2 years, 5 months ago

Yes it does! :-)

David Vreken - 2 years, 5 months ago

@David Vreken – I've added a comment on more or less how I approached the 8x4 case, but it's kind of messy and leaves a bit to the imagination... Any chance you had a cleaner approach?

Geoff Pilling - 2 years, 5 months ago

@Geoff Pilling – Unfortunately I don't have a cleaner approach, and I think I would have explained it the same way as you did. The key strategy is controlling the total number of 2x2's on the board, which you already mentioned. There may be some steps left to the imagination, but the alternative is a lengthy solution describing many of the permutations of game play, and I think anyone who has read your solution this far can probably fill in the gaps themselves.

David Vreken - 2 years, 5 months ago

I agree the only losing sizes within the interval [1,8] are 1x(2n-1), 2x4 and 2x5. The key to winning seems to be controlling regions of size 2x2, 2x3 or 3x3. If there are two of them you can counter your opponent.

For larger boards, I suspect if the smallest number is at least 3 then player 1 wins. I'm not sure about 2xn for n>8. Are they all wins for player 1?

Jeremy Galvagni - 2 years, 5 months ago

Great questions!

I'd love to generalize this for n>8... And/or give a more universal strategy that works more or less for all cases... :)

To be honest, the reason I stopped at 8, was because I was getting tired of not finding a more general solution... :-/

Geoff Pilling - 2 years, 5 months ago

I was more or less in the same boat, but am also curious if there might be a way to generalize the 2xn case for all n?

Geoff Pilling - 2 years, 5 months ago

How does strategy C apply to a 5x8 rectangle? I don't see how to remove a square and leave two identical chunks.

Varsha Dani - 2 years, 5 months ago

For a 5x8, you start by removing a 4x4 from the central region, leaving a row of 4 across the top, but you don't really care about these four since they represent an even number of moves. I.e. any time you opponent takes one of the four, you can take one, and continue with the game as you left it.

Geoff Pilling - 2 years, 5 months ago

Oh, I see, you don't mean two identical disconnected regions. Ok, now it makes sense :)

Varsha Dani - 2 years, 5 months ago

Starting with a rectangular board

The answer is 53.

1 solution

0 pending reports