Step by Step

Algebra Level 5

Let F k ( 1729 ) F_{k}^{(1729)} denote the kth Fibonacci 1729-step number . Find

log ⁡ 2 ( ∑ k = 1 ∞ F k ( 1729 ) 2 k ) \log_{2} \left(\sum_{k=1}^{\infty} \frac{F^{(1729)}_{k}}{2^{k}} \right)


The answer is 1728.

View wiki
Jake Lai by Jake Lai , 21, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Jake Lai
Jan 22, 2015

The key is generating functions . For any Fibonacci n n -step sequence { F k ( n ) } k = 0 ∞ \lbrace F_{k}^{(n)} \rbrace_{k=0}^{\infty} , the generating function is

g ( x , n ) = x 1 − x − x 2 − … − x n = ∑ k = 1 ∞ F k ( n ) x k ( ∗ ) g(x, n) = \frac{x}{1-x-x^{2}-\ldots-x^{n}} = \sum_{k=1}^{\infty} F_{k}^{(n)}x^{k} \ \ \ \ (*)

Observe that we can rewrite g ( x , n ) g(x, n) as

x 2 − x n + 1 − 1 x − 1 = x ( 1 − x ) x n + 1 − 2 x + 1 \frac{x}{2-\frac{x^{n+1}-1}{x-1}} = \frac{x(1-x)}{x^{n+1}-2x+1}

Substituting in x = 1 2 x = \frac{1}{2} gives

g ( 1 2 , n ) = 1 2 ( 1 − 1 2 ) ( 1 2 ) n + 1 − 2 ( 1 2 ) + 1 = 1 4 ( 1 2 ) n + 1 = 2 n − 1 g(\frac{1}{2}, n) = \frac{\frac{1}{2}(1-\frac{1}{2})}{(\frac{1}{2})^{n+1}-2(\frac{1}{2})+1} = \frac{\frac{1}{4}}{(\frac{1}{2})^{n+1}} = 2^{n-1}

Since our n = 1729 n = 1729 , our sum is then

∑ k = 1 ∞ F k ( 1729 ) 2 k = g ( 1 2 , 1729 ) = 2 1728 \sum_{k=1}^{\infty} \frac{F^{(1729)}_{k}}{2^{k}} = g(\frac{1}{2}, 1729) = 2^{1728}

Thus,

log ⁡ 2 ( ∑ k = 1 ∞ F k ( 1729 ) 2 k ) = log ⁡ 2 ( 2 1728 ) = 1728 \log_{2} \left(\sum_{k=1}^{\infty} \frac{F^{(1729)}_{k}}{2^{k}} \right) = \log_{2} (2^{1728}) = \boxed{1728}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Proof of ( ∗ ) (*) :

The case n = 2 n = 2 (usual Fibonacci sequence), I believe, is pretty well known (?) . Here, I will prove for general positive integer n n .

( 1 − x − … − x n ) ( ∑ k = 1 ∞ F k ( n ) x k ) = ∑ k = 1 ∞ F k ( n ) x k − ∑ k = 1 ∞ F k ( n ) x k + 1 − … − ∑ k = 1 ∞ F k ( n ) x k + n (1-x-\ldots-x^{n})\left( \sum_{k=1}^{\infty} F_{k}^{(n)}x^{k} \right) = \sum_{k=1}^{\infty} F_{k}^{(n)}x^{k}-\sum_{k=1}^{\infty} F_{k}^{(n)}x^{k+1}-\ldots-\sum_{k=1}^{\infty} F_{k}^{(n)}x^{k+n}

All the

F k ( n ) x k − F k − 1 ( n ) x k − … − F k − n ( n ) x k = F k ( n ) x k − ∑ i = 1 n F k − i ( n ) x k F_{k}^{(n)}x^{k}-F_{k-1}^{(n)}x^{k}-\ldots-F_{k-n}^{(n)}x^{k} = F_{k}^{(n)}x^{k}-\sum_{i=1}^{n}F_{k-i}^{(n)}x^{k}

disappear for k > n k > n since F k ( n ) = ∑ i = 1 n F k − i ( n ) \displaystyle F_{k}^{(n)} = \sum_{i=1}^{n} F_{k-i}^{(n)} by definition, leaving

∑ k = 1 n F k ( n ) x k − ∑ k = 1 n − 1 F k ( n ) x k + 1 − … − ∑ k = 1 1 F k ( n ) x k + n − 1 \sum_{k=1}^{n} F_{k}^{(n)}x^{k}-\sum_{k=1}^{n-1} F_{k}^{(n)}x^{k+1}-\ldots-\sum_{k=1}^{1} F_{k}^{(n)}x^{k+n-1}

Expanding the sums and doing a slight rearrangment of terms, we arrive at

F 1 ( n ) ( x − x 2 − … − x n ) + F 2 ( n ) ( x 2 − x 3 − … − x n ) + … + F n ( n ) x n = ( x − x 2 − … − x n ) + ( x 2 − x 3 − … − x n ) + … + 2 n − 2 x n = x F_{1}^{(n)}(x-x^{2}-\ldots-x^{n})+F_{2}^{(n)}(x^{2}-x^{3}-\ldots-x^{n})+\ldots+F_{n}^{(n)}x^{n} = (x-x^{2}-\ldots-x^{n})+(x^{2}-x^{3}-\ldots-x^{n})+\ldots+2^{n-2}x^{n} = x

because F 1 ( n ) = 1 F_{1}^{(n)} = 1 and F k ( n ) = 2 k − 2 F_{k}^{(n)} = 2^{k-2} for all 2 ≤ k ≤ n 2 \leq k \leq n . You will see that the terms eventually cancel out.

After that arduous journey of algebraic manipulation, we finally get that

( 1 − x − … − x n ) ( ∑ k = 1 ∞ F k ( n ) x k ) = x (1-x-\ldots-x^{n})\left( \sum_{k=1}^{\infty} F_{k}^{(n)}x^{k} \right) = x

and thus

g ( x , n ) = ∑ k = 1 ∞ F k ( n ) x k = x 1 − x − … − x n \boxed{\displaystyle g(x, n) = \sum_{k=1}^{\infty} F_{k}^{(n)}x^{k} = \frac{x}{1-x-\ldots-x^{n}}}

(I hate the world.)

Jake Lai - 6 years, 4 months ago

Log in to reply

You could try to derive a general formula for the sequence:

F n = ∑ j = 1 p F n − j k j { F }_{ n }=\sum _{ j=1 }^{ p }{ { F }_{ n-j } } { k }_{ j }

If you want to torture yourself again?

Julian Poon - 6 years, 4 months ago

Log in to reply

I might be doing a generalisation of this result for SMPF :D

Jake Lai - 6 years, 4 months ago

Log in to reply

@Jake Lai – Its gonna fail in Creativity and originality Applicability and relevance. And you need to pay so much... I don't know for your school but my school never pays for us to represent them in maths or science. Except for crappy NSC, which nobody want's to go because of it's stupid and biased way of judging.

Julian Poon - 6 years, 4 months ago
Aareyan Manzoor
Mar 4, 2015

first, let F k ( 1729 ) = R k F^{(1729)}_k=R_k first we note that, R k + R k + 1 + R k + 2 + . . . . . R k + 1728 = R k + 1729 R_{k}+R_{k+1}+R_{k+2}+.....R_{k+1728}=R_{k+1729} now. let S = R 1 2 + R 2 4 + R 3 8 + R 4 16 . . . . . S=\dfrac{R_{1}}{2}+\dfrac{R_{2}}{4}+\dfrac{R_{3}}{8}+\dfrac{R_{4}}{16}..... we now calculate S = R 1 2 + R 2 4 + R 3 8 + R 4 16 . . . . . 2 S = R 1 + R 2 2 + R 3 4 + R 4 8 . . . . . 4 S = 2 R 1 + R 2 + R 3 2 + R 4 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1728 S = 2 2727 R 1 + 2 2726 R 2 . . . . . . + R 2728 + R 1729 2 + R 1730 4 . . . . . \begin{aligned} &S=&\dfrac{R_{1}}{2}&+\dfrac{R_{2}}{4}&+\dfrac{R_{3}}{8}&+\dfrac{R_{4}}{16}.....\\ &2S=&R_{1}&+\dfrac{R_{2}}{2}&+\dfrac{R_{3}}{4}&+\dfrac{R_{4}}{8}.....\\ &4S=&2R_{1}&+R_{2}&+\dfrac{R_{3}}{2}&+\dfrac{R_{4}}{4}.....\\ &.....&...&.............&.............&......\\ &2^{1728}S=&2^{2727}R_{1}&+2^{2726}R_{2}&......+R_{2728}&+\dfrac{R_{1729}}{2}+\dfrac{R_{1730}}{4}.....\\ \end{aligned} note that 2 n + 2 n − 1 + 2 n − 2 + . . . . . . + 2 + 1 = 2 n + 1 − 1 2^n+2^{n-1}+2^{n-2}+......+2+1=2^{n+1}-1 adding all 1729 equations ( 2 1729 − 1 ) S = ( 2 1728 − 1 ) R 1 + ( 2 1727 − 1 ) R 2 . . . . . . + ( 2 − 1 ) R 1728 + R 1 + R 2 + R 3 . . . . . . + R 1729 2 + R 2 + R 3 + R 4 . . . . . . + R 1730 4 . . . . . . . (2^{1729}-1)S=(2^{1728}-1)R_{1}+(2^{1727}-1)R_{2}......+(2-1)R_{1728}+\dfrac{R_{1}+R_{2}+R_{3}......+R_{1729}}{2}+\dfrac{R_{2}+R_{3}+R_{4}......+R_{1730}}{4}....... re-writing, ( 2 1729 − 1 ) S = 2 1728 R 1 + 2 1727 R 2 + . . . . . + 2 R 1728 − ( R 1 + R 2 + R 3 . . . . . . + R 1728 ) + R 1730 2 + R 1731 4 . . . (2^{1729}-1)S=2^{1728}R_{1}+2^{1727}R_{2}+.....+2R_{1728}-(R_{1}+R_{2}+R_{3}......+R_{1728})+\dfrac{R_{1730}}{2}+\dfrac{R_{1731}}{4}... for subtraction, 2 ∗ 2 1728 S = 2 2728 R 1 + 2 2727 R 2 . . . . . . + 2 R 2728 + R 1729 + R 1730 2 . . . . 2*2^{1728}S= 2^{2728}R_{1}+2^{2727}R_{2}......+2R_{2728}+R_{1729}+\dfrac{R_{1730}}{2}.... subtracing 2 equations, 2 1729 S − ( 2 1729 − 1 ) S = R 1729 + ( R 1 + R 2 + R 3 . . . . . . + R 1728 ) 2^{1729}S-(2^{1729}-1)S =R_{1729}+(R_{1}+R_{2}+R_{3}......+R_{1728}) S = R 1729 + R 1730 − R 1729 = R 1730 = F 1730 ( 1729 ) S=R_{1729}+R_{1730}-R_{1729}=R_{1730}=F_{1730}^{(1729)} note this 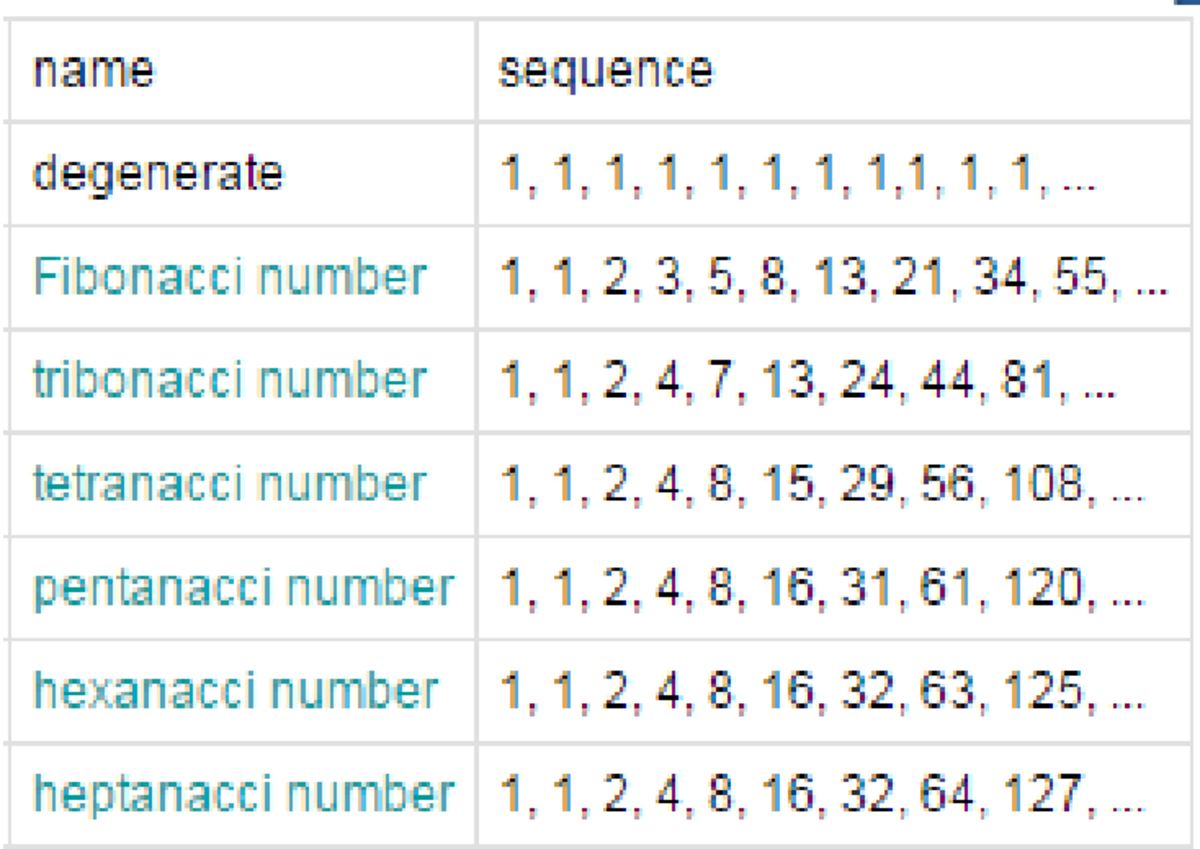we can say that F k n = { 1 , k = 1 2 k − 2 , 1 < k ≤ n + 1 ∑ x = 1 n ( F k − x n ) , k ≥ n + 1 F^{n}_k=\begin{cases} 1, &k=1\\ 2^{k-2},& 1<k\leq n+1\\ \sum_{x=1}^{n} (F^{n}_{k-x}),&k\geq n+1 \end{cases} hence, F 1730 1729 = 2 1730 − 2 = 2 1728 F^{1729}_{1730}=2^{1730-2}=2^{1728} and l o g 2 ( 2 1728 ) = 1728 log_2 (2^{1728})=\boxed{1728}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Did the same! Well, you are quite good, really at 13!

Kartik Sharma - 6 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...