Stop or Go
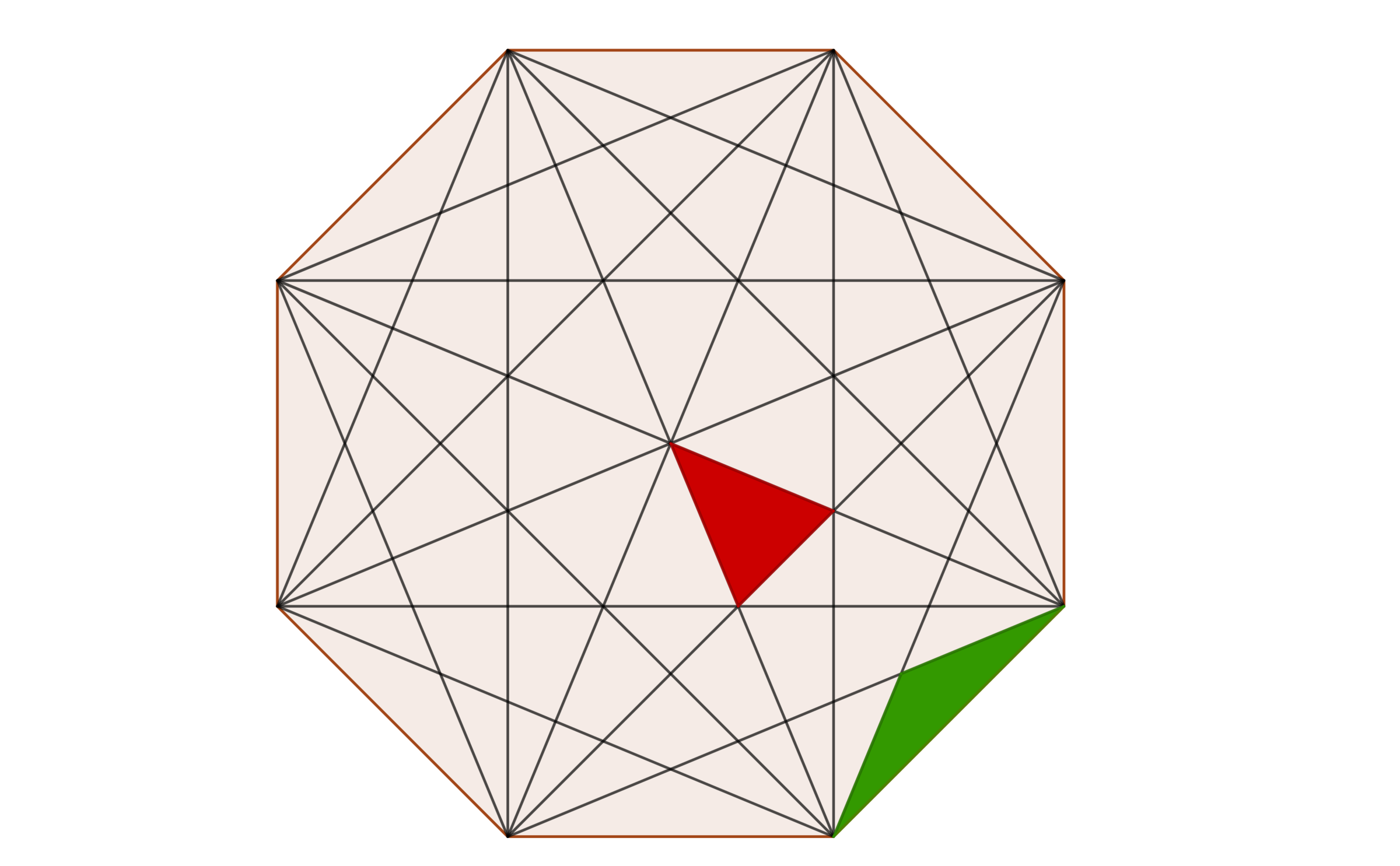
In this regular octagon, which triangle has the greater area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Log in to reply
Rotate just the greenie around center
Log in to reply
Log in to reply
@Jason Gomez – Thank you for this visual, Jason! The 1-hour soap opera just ended, lunch is more delicious with more drama, sorry I can't express my appreciation faster. Thanks again! 👏👍💪🏼🤗💖
I can see everything required from this picture, I assume the part of the explanation which confused me a lot was the 1 8 0 0 base part (still have no clue on what that meant)
Log in to reply
@Jason Gomez – Red's 45° + Green's 135° = 180° as the base of newly created double area right triangle.
@Jason Gomez – Easier to see their equality with shared height and side-by-side half base.
Log in to reply
@Saya Suka – I can see it now in both ways, was quite blind before
What do you use to make images and stuff? Look really cool :)
Log in to reply
I use notability (about 10$) on my iPad
Log in to reply
@Jason Gomez – I use this device to take down class notes and other educational stuff, so that’s the reason I bought this app (Notes is just too bad)
Log in to reply
@Jason Gomez – True facts, default note-taking apps suck...
@Jason Gomez – Oh, nice. I guessed it would be Notability, saw the similarity with Andrew Last's solutions.
Simple approach - sin(3pi/7)=sin(pi/7).
Log in to reply
Same sines, and then what? How do I know if the sides are the same without a compass? 1/4 = 3/4, right?
Where did you get the 7 π I can only get the angles in multiples of 1 6 π
Two Sides of green triangle and two Sides of red triangle - equal.
Log in to reply
Any proof of that?
Log in to reply
Simple exercise for students
@Saya Suka Could you help me in this problem , I think I am close to the solution but at the same time feel very far away
Excuse my mistake - sin(2pi/8)=sin(3 2pi/8), and green and red areas equal a a * sin(2pi/8)/2
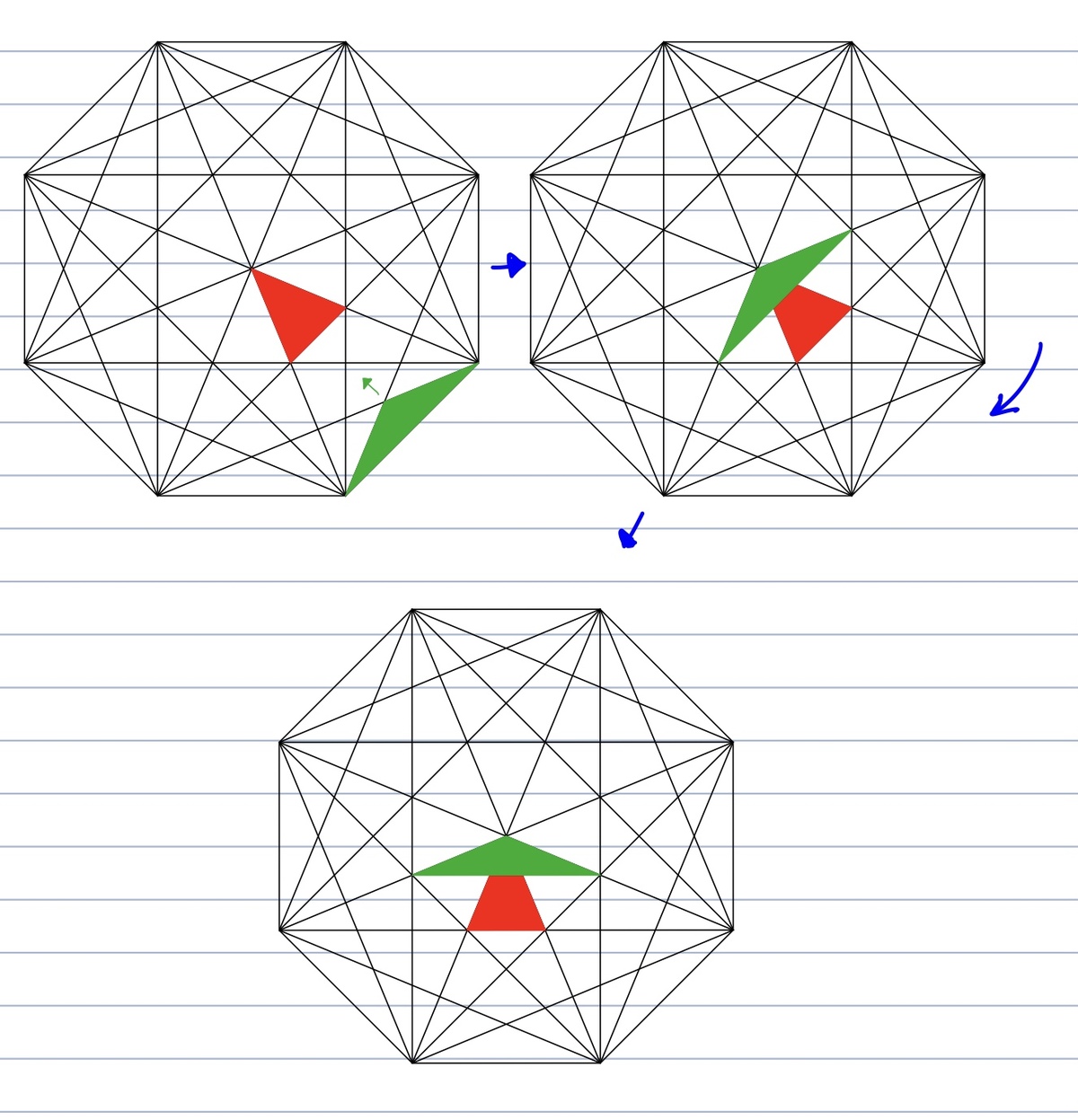
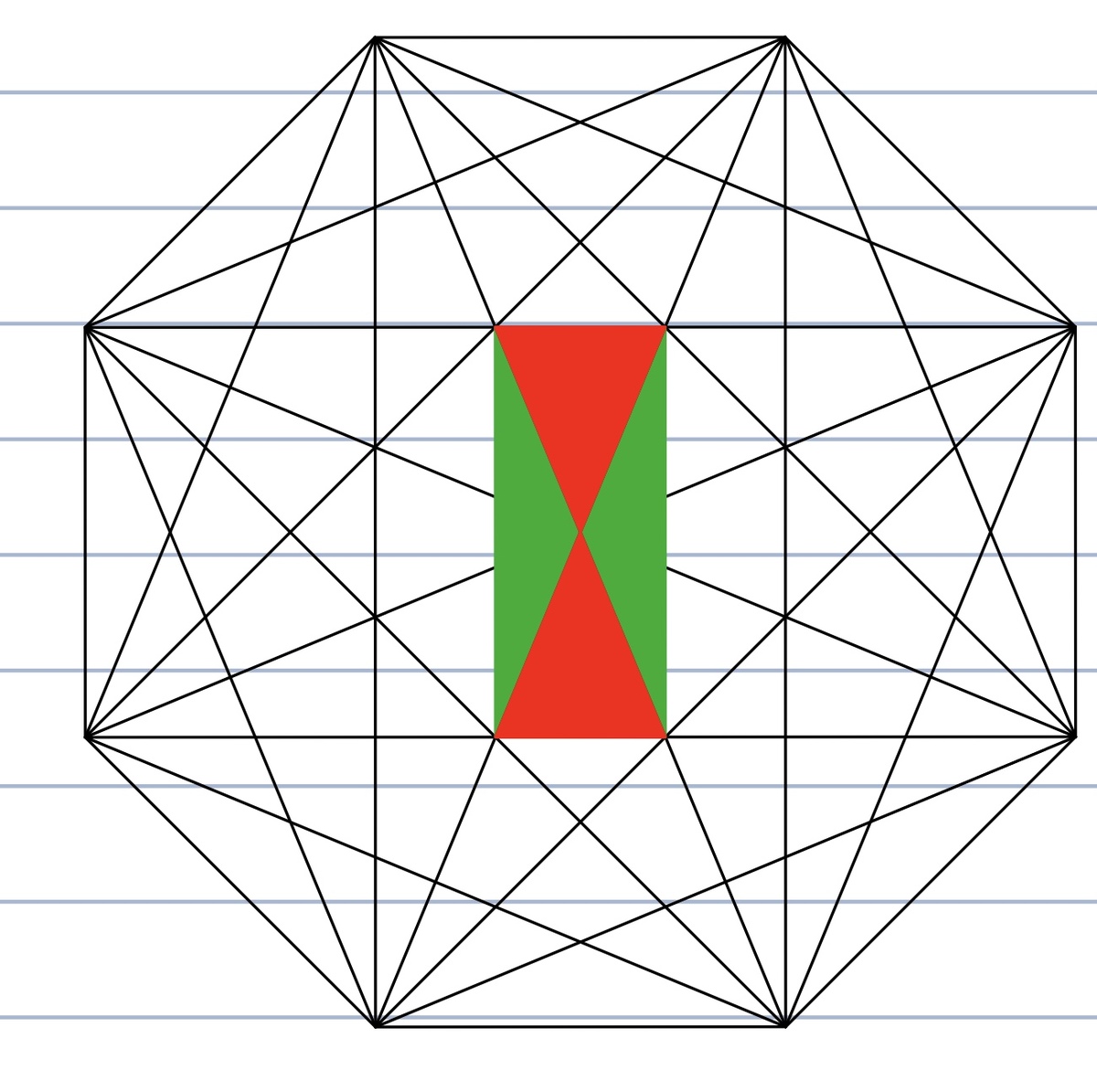
If we rotate the octagon 22.5° clockwise, both the red and green triangles will have their bases parallel horizontally. Then, it's easier seen with all the parallel lines that the green triangle is similar to the larger obtuse triangle where the red lies inside, sharing its base (spanning from one octagonal vertex to another) and its peak (highest vertex). Once the picture is seen, we can mentally slide and push the green triangle along the two parallel lines up until the green's peak meet the red's peak (which is also the octagon's center). Done with the upwards translation, we start a rotation of 90° of either direction. The triangles will produce a 180° base together (we can already see this at the end of the previous translation with red's peak taking one angle of 45° –as clearly from the word octagon– and noting that the green's peak occupying 3 times of the red's peak angle) and the new triangle formed by them has twice the base length and the same height.