Storm Water Detention Tank with Two Orifices for Outflow
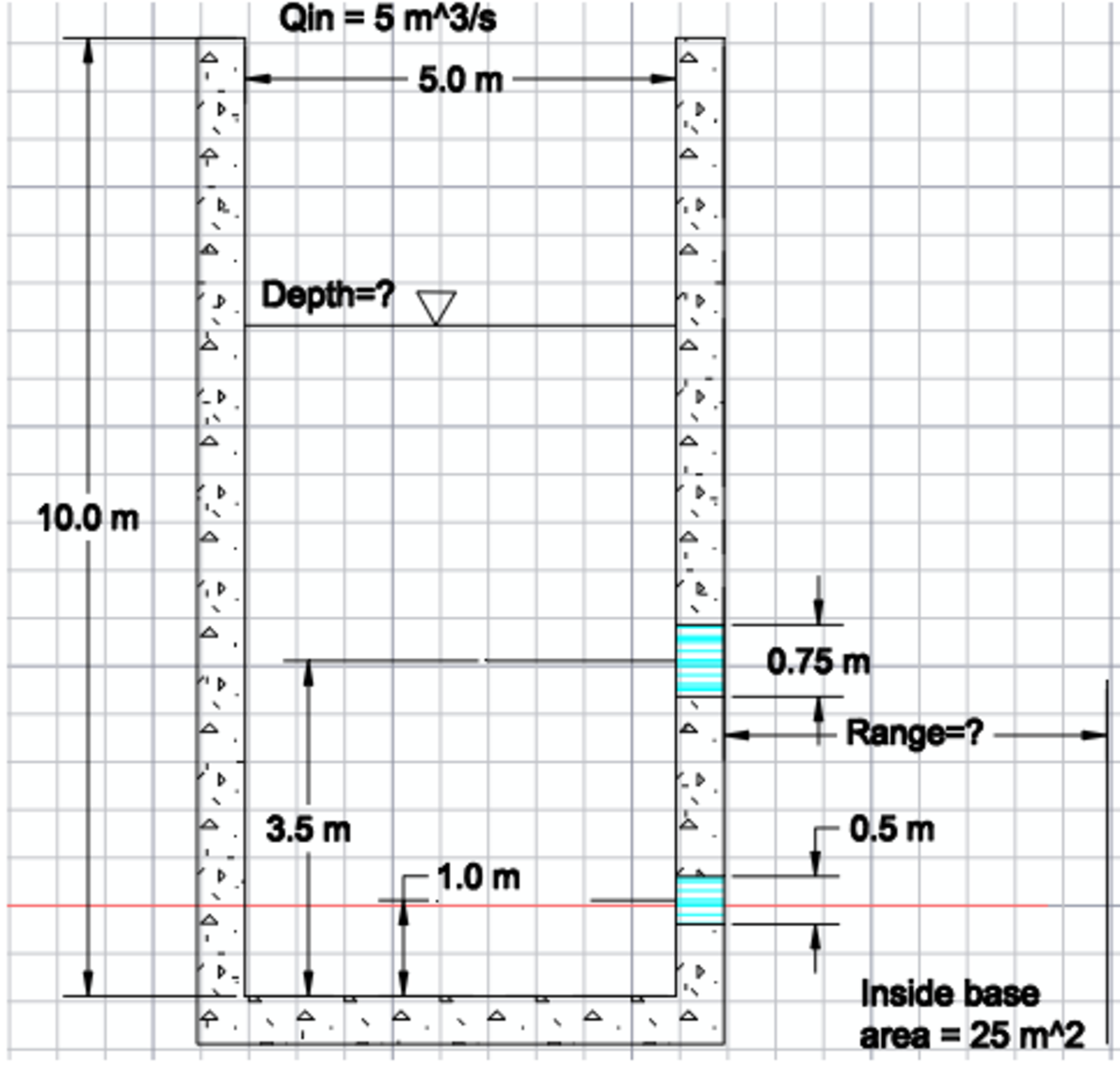 A storm water detention tank collects storm water from a paved area at a maximum, constant rate of 5 m^3/s at t=0 seconds. The tank is 10 meters high and has an inside base area of 5 m by 5 m. The 1st orifice has a diameter of 50 cm and is 1 m above the tank base. The 2nd orifice has a diameter of 0.75 m and is 3.5 m above the tank base. What is the range from the tank the water from the 2nd orifice meets with the ground at t=30 seconds? Assume steady flow occurs within the tank and neglect any weir flow from orifices before orifice flow fully develops. The ground surrounding the tank is the same elevation as the inside of the tank bottom. Take g=9.81 m/s^2, and Cd=0.62 (entrance coefficient). Please provide your answer to the nearest 1/10th of a meter.
A storm water detention tank collects storm water from a paved area at a maximum, constant rate of 5 m^3/s at t=0 seconds. The tank is 10 meters high and has an inside base area of 5 m by 5 m. The 1st orifice has a diameter of 50 cm and is 1 m above the tank base. The 2nd orifice has a diameter of 0.75 m and is 3.5 m above the tank base. What is the range from the tank the water from the 2nd orifice meets with the ground at t=30 seconds? Assume steady flow occurs within the tank and neglect any weir flow from orifices before orifice flow fully develops. The ground surrounding the tank is the same elevation as the inside of the tank bottom. Take g=9.81 m/s^2, and Cd=0.62 (entrance coefficient). Please provide your answer to the nearest 1/10th of a meter.
The answer is 2.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
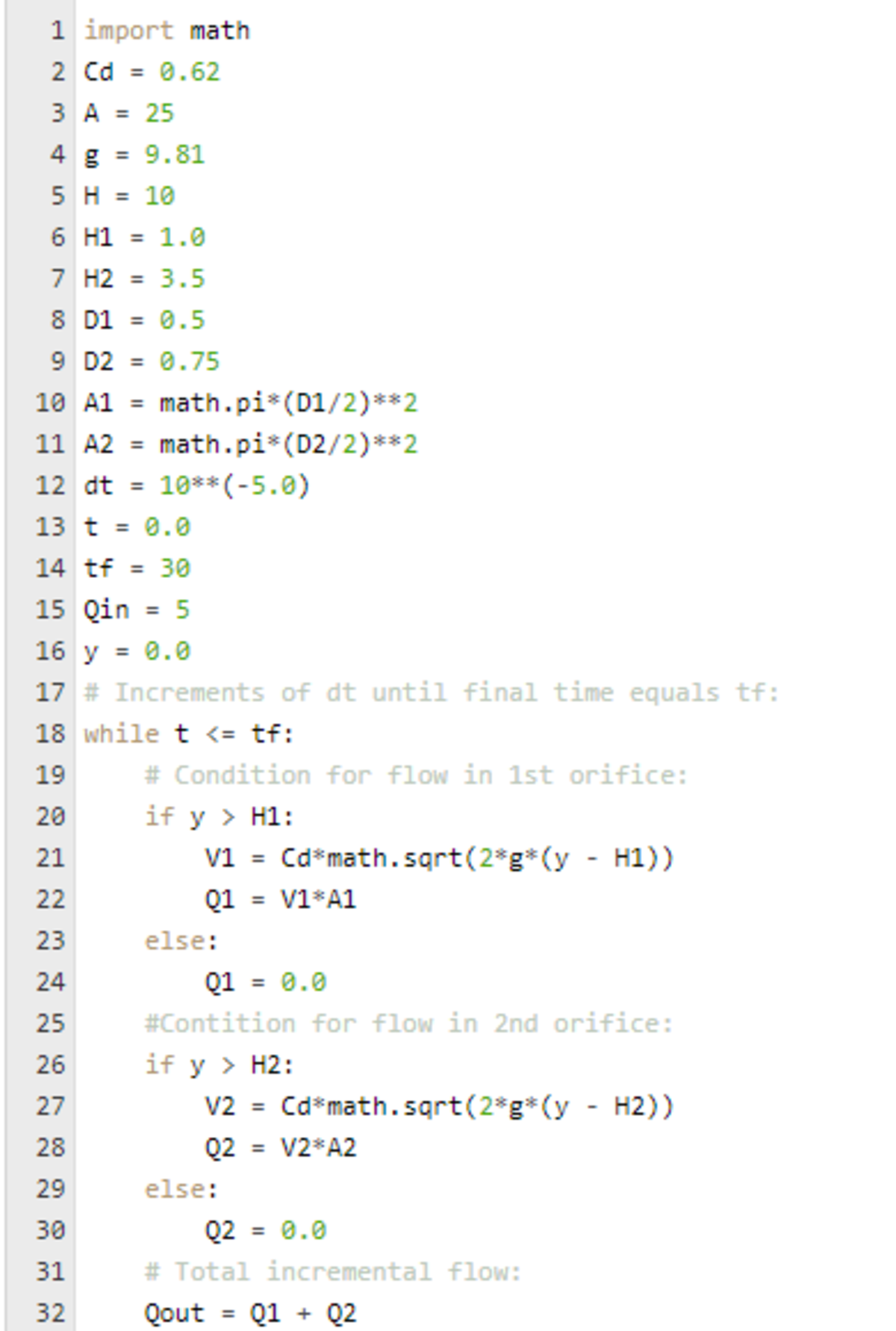
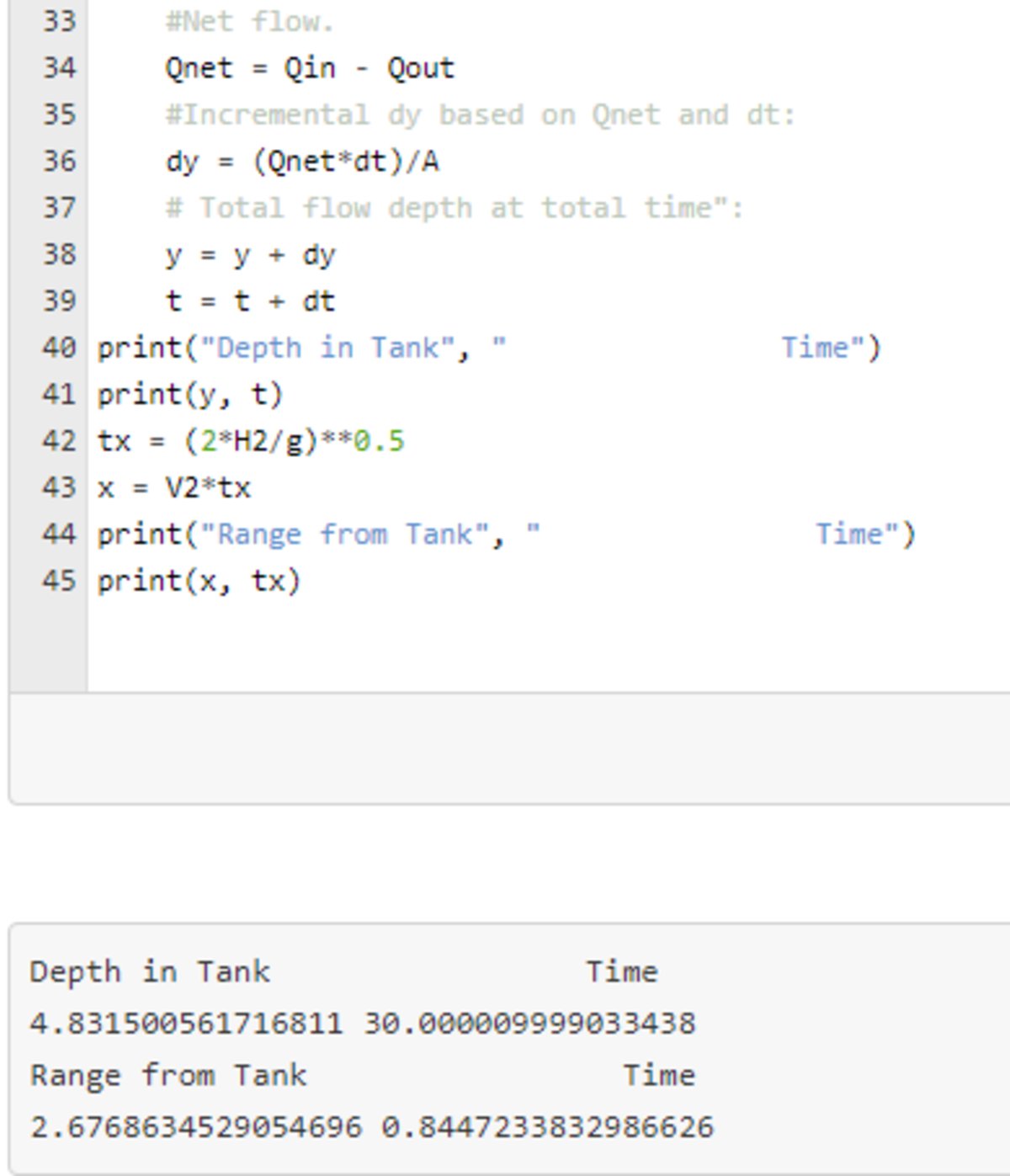
This was a fun problem. I ran a time simulation using Toricelli's Law and some conditional statements. Results are printed at the end. Water flows through an orifice if the water level is higher than the orifice. And then the flow speed and flow rate depend on the water level relative to the orifice center.