Storming Tiling
Let a be a tile just like a domino but instead. You have a board split up into unit squares to cover only using strominos. Each unit square on the board can be overlapped using strominos once or twice but not more. What is the maximum number of strominos you can use to tile up the board so that at least each unit square is covered once?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
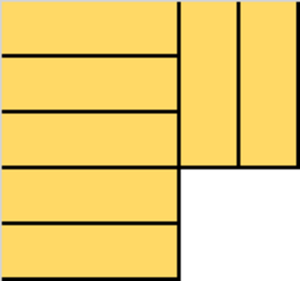
Since the board has 2 5 squares, we can use at most 8 strominos. The following configuration shows this is possible:
Now, we can't simply overlay another copy of this (using 1 6 strominos); this would leave the centre square uncovered, which isn't allowed.
The interesting part of this problem is showing that the only way to cover the board using 8 strominos is to leave the centre square uncovered. To show this, first label the board as follows:
Each stromino covers a 1 , a 2 and a 3 . There are nine 2 s on the board, so in a covering of eight strominos, one of these must be left uncovered.
Now relabel the board:
Each stromino covers an A , a B and a C . There are nine B s on the board, so in a covering of eight strominos, one of these must be left uncovered.
The only square labelled with both a 2 and a B is the centre square; therefore this one must be left uncovered in a tiling by eight strominos.
Finally, note that we can easily cover the centre square if we use seven strominos:
Overlaying the two configurations gives a permitted tiling using the maximum 1 5 strominos.