Story of Sinx and Flux
A particle with charge
q
=
+
1
0
is position at
N
(
x
,
y
,
z
)
=
(
3
,
2
,
1
)
at that orange dot as shown in figure. Find the flux through the surface area enclosed by two equation
y
=
0
and
y
=
s
i
n
x
(
0
≤
x
≤
2
π
)
for the one cycle only, from point
A
to point
B
.
 Details and Assumptions
1) Electric permittivity
ϵ
o
=
1
Details and Assumptions
1) Electric permittivity
ϵ
o
=
1
The answer is 0.185.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath
I have attached the solution of the question which you reported today. Just take
C
1
=
C
and
C
2
=
C
0
.
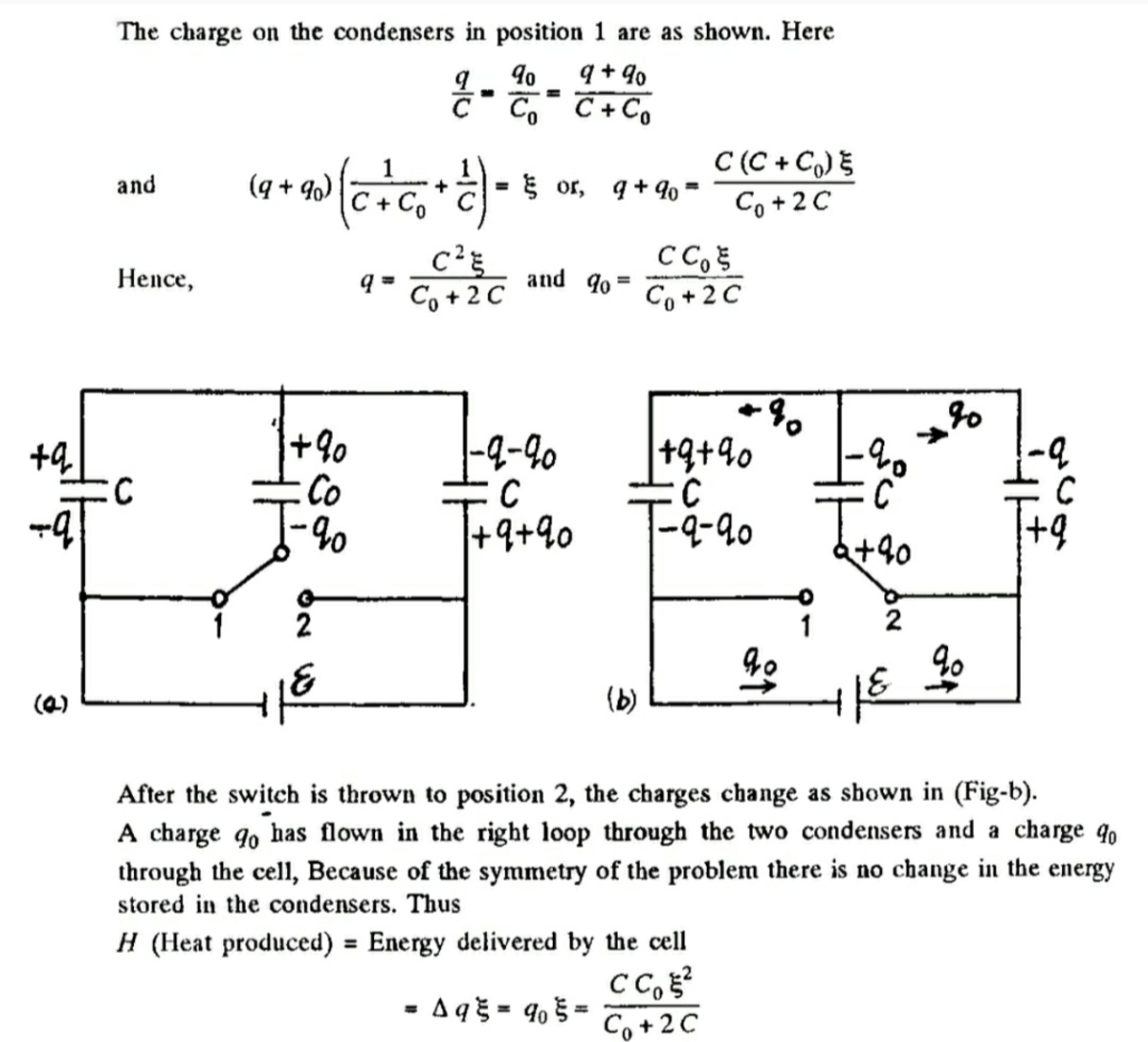
Thank you for your comment. Firstly, I did not ask for the solution. Secondly, I request you to carefully read what I mentioned in the report. The notion of heat being generated in the circuit is completely incorrect. The energy supplied by the source is simply stored in the capacitors. The form of energy supplied is not heat energy, but it is electrical energy.
When the position of the switch changes, the charges get re-distributed and therefore there is no change in the total energy of the capacitors. Even your solution says this, as did I. So, if the cell supplies electrical energy, and if the electrical energy stored in the capacitors is conserved, then how is heat generated? In electrical circuits comprising of inductors, capacitors and resistors, the only element capable of generating heat is a resistor. This circuit has none, so no heat can be generated. Hope I am able to explain this. Basically, the solution you posted is conceptually flawed.
I solved for the charges on the capacitors and verified that energy is conserved. I did not need a solution.
Also, since energy is conserved, the cell does not supply extra energy when the position of the switch changes. The charges simply re-distribute so that the law of conservation of charge remains obeyed.
Log in to reply
Comment has been edited.
Log in to reply
Hmm so I think I need to change the name of question as electrial energy generated?? Correct??
Log in to reply
@A Former Brilliant Member – Yes, the question needs re-phrasing. Moreover, the answer is also wrong, I think. A better question would be to not ask for total energy differences between position A and B since they are the same but instead ask for the difference in charge in one of the capacitors.
Consider a point on the X-Y plane having a position vector:
r p = x i ^ + y j ^
The location of the charge is:
r c = 3 i ^ + 3 j ^ + k ^
The vector joining these two points and directed away from the charge is:
r = r p − r c
An elementary area around this point can be defined as:
d S = − d y d x k ^
The electric field at the point P is:
E = 4 π q ∣ r ∣ 3 r
The flux through the elementary area is:
d ϕ = E ⋅ d S
Substituting all expressions and simplifying and integrating leads to the following expression for flux through the given area:
ϕ = 4 π q ⎝ ⎜ ⎛ ∫ 0 π ∫ 0 sin x ( ( x − 3 ) 2 + ( y − 2 ) 2 + 1 ) 3 / 2 d y d x + ∫ π 2 π ∫ sin x 0 ( ( x − 3 ) 2 + ( y − 2 ) 2 + 1 ) 3 / 2 d y d x ⎠ ⎟ ⎞ ≈ 0 . 1 8 5