Straight Line Through A Grid
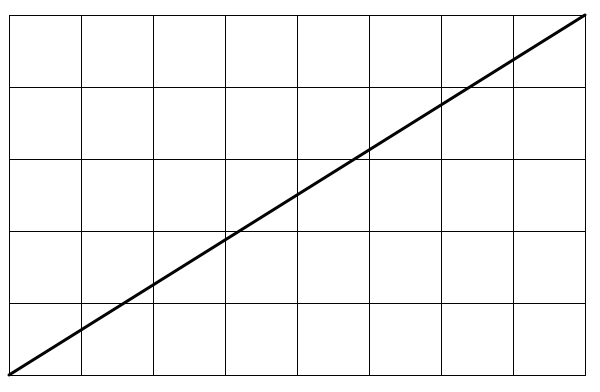
If we draw a line connecting the corners of a square grid, how many squares does it cut through?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you look at the image and count, you will get that the answer is 12. How can we generalize the result?
Look at the line. When does it enter a new square? It enters a new square whenever it crosses a grid line, whether vertically or horizontally. It starts out (in the corner) of a square, and then it has to cross 4 + 7 grid lines, before ending in the corner of the rectangle. Thus, it will go through 1 + 4 + 7 = 1 2 squares.
More generally, for a m × n grid, where g cd ( m , n ) = 1 , then the line will not hit any other corners, and hence each time it crosses a gridline, it will go into a new square. Thus, the number of squares is 1 + ( m − 1 ) + ( n − 1 ) = m + n − 1 .
How do we deal with the case where g cd ( m , n ) = 1 ?