Straight To Circumference?

Geometry Level 2

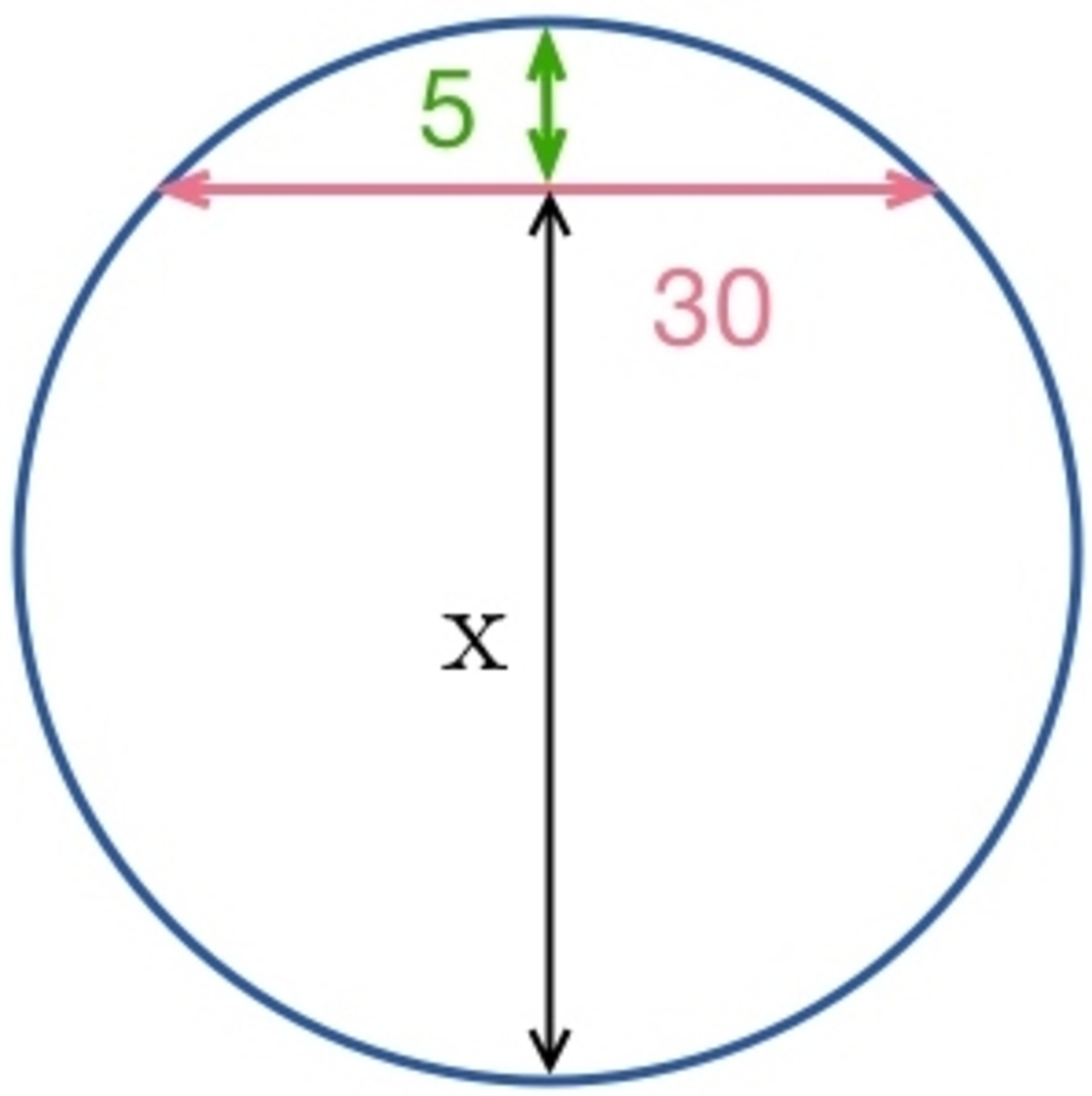
A circle has a chord $30 \text{ cm}$ long and the radius of the circle is $5\text{ cm}$ more than the perpendicular distance from the center of the circle to the chord. What is the circumference of the circle?

Give your answer to 3 decimal places.

The answer is 157.0796327.

4 solutions

E Tyson Ewing Iii
May 31, 2016

The radius drawn perpendicular to a chord bisects a chord. A right triangle can be made by drawing the radii perpendicular to the chord and to an endpoint of the chord. Let the sides of the triangle be $x$ , $15$ , and $x+5$ . Setting up and equation, using the pythagorean theorem, we have:

${x^{2} + 15^{2} = (x+5)^{2}}$

${x^{2} + 225 = x^{2} +10x + 25}$

${200 = 10x}$

${20 = x}$

Thus, the radius of the circle is $25 cm$ , since the radius is $x+5$ , and the circumference is $\boxed{157.0796327}$

@E Tyson Ewing III

Can you please explain what you meant to say "edge of a circle" in the statement of the problem? And how could you assume the two other sides of the right triangle as x, x+15?

Sandeep Bhardwaj - 5 years ago

In the high school geometry class that I teach, I have made it a habit of saying edge of the circle when referring to the circumference.

The triangle is made by the radius, the radius perpendicular to the chord, and the chord itself. Since the perpendicular radius bisects the chord, a side of the triangle has length 15 cm. Since the chord is 5 cm away from the circumference of the circle, we can call its distance from the center x and the length of the radius x + 5. Hope this clarifies things for you.

E Tyson Ewing III - 5 years ago

Okay, thanks for clarifying. Since "edge" of a circle is not defined, in general, so I've edited the problem for clarity.

Sandeep Bhardwaj - 5 years ago

@Sandeep Bhardwaj – No problem. Thanks for editing the problem. I've been busy with finals.

E Tyson Ewing III - 5 years ago

Also, the sides are not x and x + 15. They are x, 15, and x + 5.

E Tyson Ewing III - 5 years ago

Michael Fuller
Jun 16, 2016

If two chords intersect in a circle, then the products of the measures of the chord segments are equal. This tells us $15 \times 15 = 5x \Rightarrow x=45$

The diameter of the circle is $d=5+x=50$

The circumference is therefore $\pi d = 50 \pi \approx \large \color{#20A900}{\boxed{157.08}}$

Matteo Monzali
May 31, 2016

The angle subtended to the chord is $\alpha=2*\tan^{-1}(\frac{15}{5})$ so the radius is $r=\frac{30}{2 * sin \alpha}=25$ and the circumference $C=2 \pi r \approx 157$

Your answer is correct. However, there is a tiny mistake.

If $x = tan^{-1}(15/5)$ , then $r = 30/(2*sin(x)) = 25$ .

E Tyson Ewing III - 5 years ago

Thanks I confused the radius with the diameter

Matteo Monzali - 5 years ago

I know. My students do it all the time. That's why I led with "Your answer is correct."

E Tyson Ewing III - 5 years ago

Amed Lolo
Jun 24, 2016

connect interestion points between the circle and the chord to center of the circle and the highest point of the circle.project a perpendicular line from the highest point to the center of the chord ,,this line will reach to center of circle there will be a right angle triangle it's members (R,,15,,15-R) so R^2=15^2+(15-R)^2 so 10R=250 ,,,,R=25 so the circumference =50π=157.0796###

Straight To Circumference?

The answer is 157.0796327.

4 solutions

0 pending reports