Strange cyclic quadrilateral
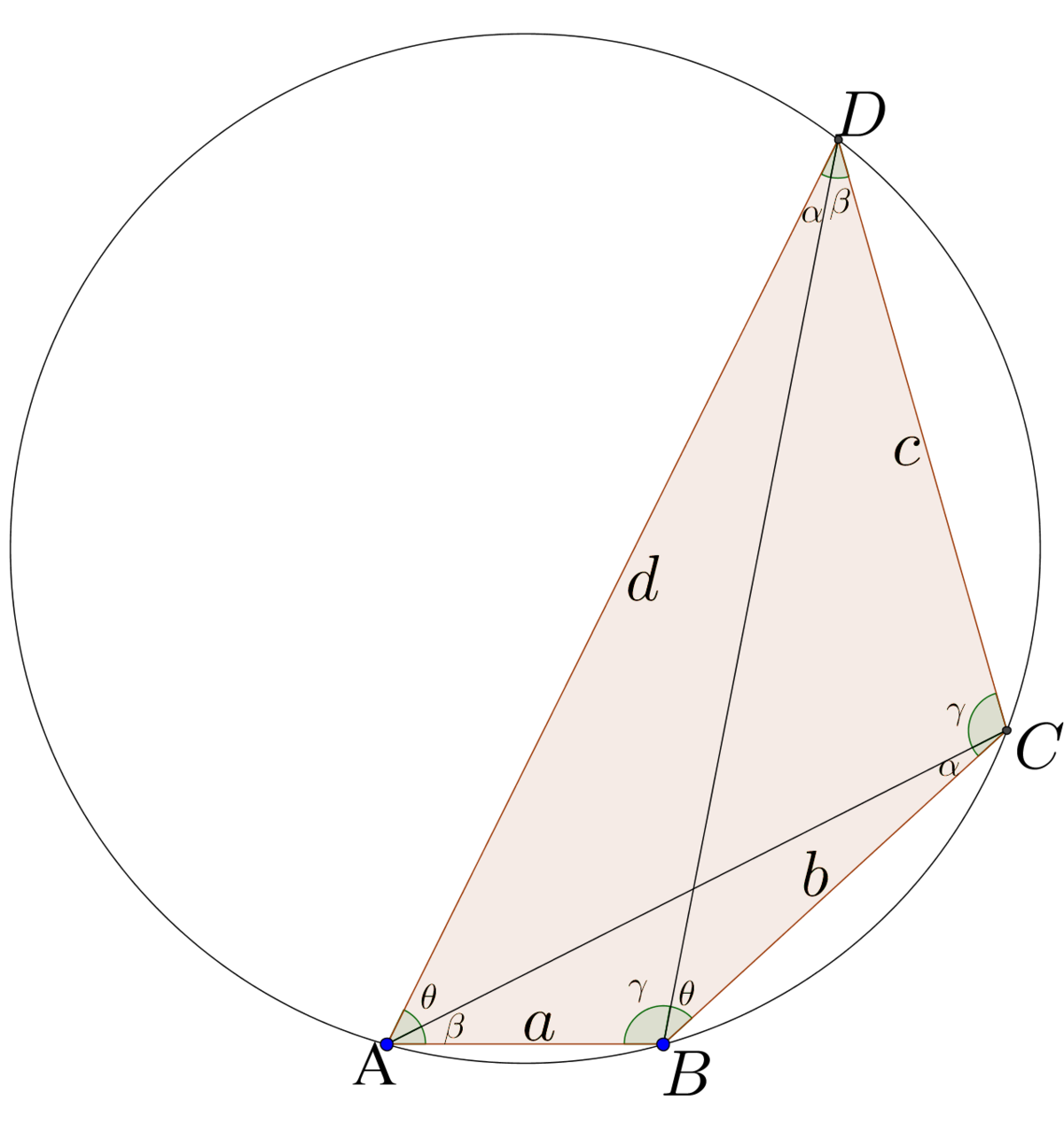 Let
A
B
C
D
be a
cyclic quadrilateral
, where
A
B
=
a
,
B
C
=
b
,
C
D
=
c
,
D
A
=
d
and
a
<
b
<
c
<
d
. Let
∠
B
C
A
=
∠
B
D
A
=
α
,
∠
B
A
C
=
∠
B
D
C
=
β
,
∠
A
B
D
=
∠
A
C
D
=
γ
and
∠
C
A
D
=
∠
C
B
D
=
θ
.
Let
A
B
C
D
be a
cyclic quadrilateral
, where
A
B
=
a
,
B
C
=
b
,
C
D
=
c
,
D
A
=
d
and
a
<
b
<
c
<
d
. Let
∠
B
C
A
=
∠
B
D
A
=
α
,
∠
B
A
C
=
∠
B
D
C
=
β
,
∠
A
B
D
=
∠
A
C
D
=
γ
and
∠
C
A
D
=
∠
C
B
D
=
θ
.
Let the equation x 4 − 2 4 x 3 + 2 0 1 x 2 − 6 9 8 x + 8 4 4 = 0 has roots a , b , c and d .
If the value of sin α + sin θ + sin γ + sin β can be written as n m , where m and n are positive integers with n -square-free, find m + n .
Note: Such quadrilateral indeed exists, the image is up to scale.
The answer is 74317.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Alan Enrique Ontiveros Salazar What was strange about this cyclic quadrilateral though?
Log in to reply
Maybe not strange about a particular cyclic quadrilateral, but the fact that such an explicit expression in terms of the coefficients of the 4 th degree polynomial for the answer even exists, which I had guessed had to be the case from the beginning. Working out the details had me thinking for some time. Kudos for Mark Henning's clear exposition of the solution.
I think this is a truly a classic problem.
Log in to reply
Both the numerator and the denominator inside the square root of the expression for R are symmetric polynomials in a , b , c , d . As such (this is standard theory), they must be expressible in terms of the elementary symmetric polynomials a + b + c + d , a b + a c + a d + b c + b d + c d , a b c + a b d + a c d + b c d and a b c d . Calculating the details is a matter of determination!
Log in to reply
@Mark Hennings – At first I thought maybe it worked for just that polynomial in particular, and then later realized it's more like what you just said. How else can such a "neat" value for the solution be accounted for? I can't recall the last time I encountered such a connection between the coefficients of a 4 t h degree polynomial with the value of a trigonometric expression in relation to a geometrical problem. Very interesting.
I agree. Took me a day to realise that the question can actually be solved without finding the roots explicitly. My approach was slightly different (not shorter though).
Log in to reply
@A Former Brilliant Member – I have to admit that at first, I said, "Is this even real?" Took me a while to confirm that it was.
It was just the title of the problem, no special reason.
By the (extended) Sine Rule, applied to appropriate triangles (all of which have the same circumcircle as the cyclic quadrilateral):
sin α a = sin β b = sin θ c = sin γ d = 2 R
where R is the radius of the circumcircle of the cyclic quadrilateral. Thus X = sin α + sin β + sin γ + sin θ = 2 R a + b + c + d Now a , b , c , d are the zeros of the polynomial f ( X ) = X 4 − 2 4 X 3 + 2 0 1 X 2 − 6 9 8 X + 8 4 4 , and hence a + b + c + d = 2 4 , so that X = R 1 2 .
The circumradius of a cyclic quadrilateral with sides a , b , c , d is
R = 4 1 ( s − a ) ( s − b ) ( s − c ) ( s − d ) ( a b + c d ) ( a c + b d ) ( a d + b c )
where s = 2 1 ( a + b + c + d ) is the semiperimeter. But a 2 + b 2 + c 2 + d 2 a 2 b 2 c 2 + a 2 b 2 d 2 + a 2 c 2 d 2 + b 2 c 2 d 2 ( a b + c d ) ( a c + b d ) ( a d + b c ) ( s − a ) ( s − b ) ( s − c ) ( s − d ) = = = = = = = ( a + b + c + d ) 2 − 2 ( a b + a c + a d + b c + b d + c d ) 2 4 2 − 2 × 2 0 1 = 1 7 4 ( a b c + a b d + a c d + b c d ) 2 − 2 a b c d ( a b + a c + a d + b c + b d + c d ) 6 9 8 2 − 2 × 8 4 4 × 2 0 1 = 1 4 7 9 1 6 a b c d ( a 2 + b 2 + c 2 + d 2 ) + ( a 2 b 2 c 2 + a 2 b 2 d 2 + a 2 c 2 d 2 + b 2 c 2 d 2 ) 8 4 4 × 1 7 4 + 1 4 7 9 1 6 = 2 9 4 7 7 2 f ( s ) = f ( 1 2 ) = 6 7 6 and hence R = 4 1 6 7 6 2 9 4 7 7 2 = 5 2 7 3 6 9 3 and hence X = 7 3 6 9 3 1 2 × 5 2 = 7 3 6 9 3 6 2 4 making the answer 7 4 3 1 7 .