Strange hexagon

Probability Level 5

Find the number of triangles (excluding degenerate triangles) in the given figure.

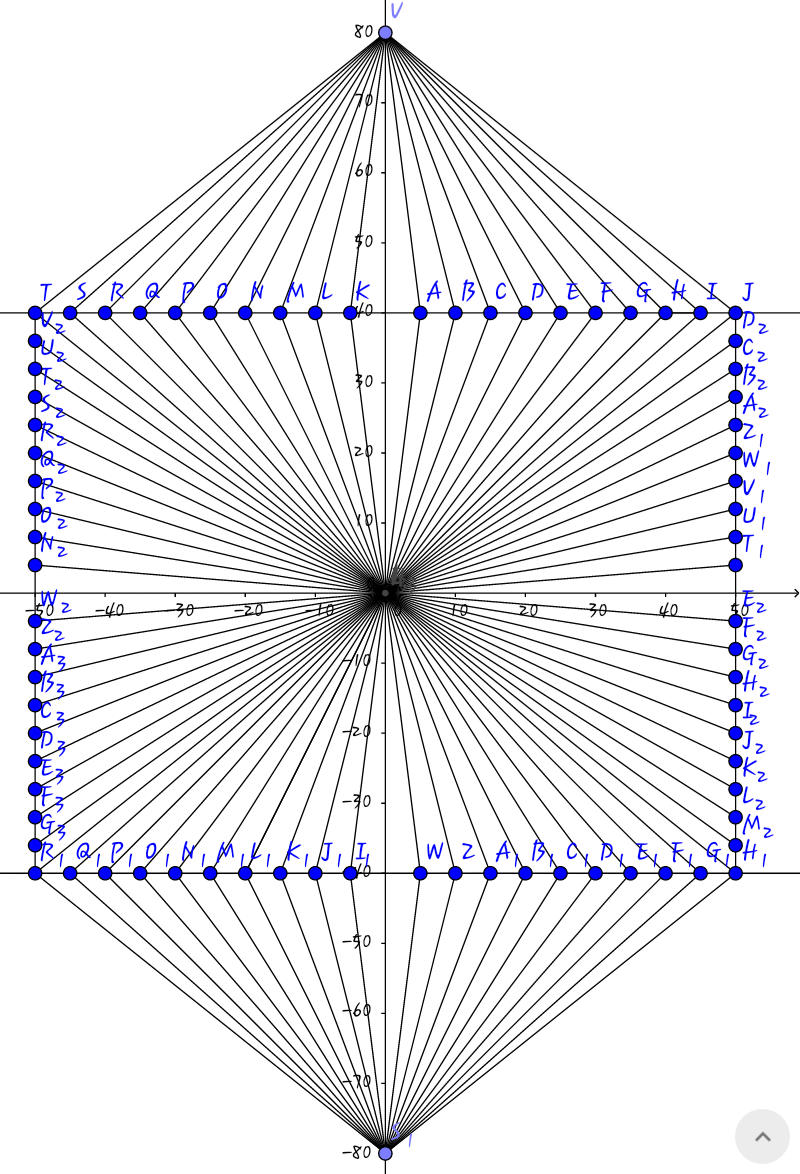
In the given figure, $VTR_1S_1H_1J$ is a hexagon, such that :-

There are $19$ defined points on $TJ$ (excluding $T$ and $J$ ) which are connected to $V$ and $O$ (the geometric center of the hexagon) by line segments such that $V$ is on opposite side of $TJ$ as compared to $O$ .

Similarly, there are $19$ defined points on $R_1H_1$ (excluding $R_1$ and $H_1$ ) which are connected to $S_1$ and $O$ (the geometric center of the hexagon) by line segments such that $S_1$ is on opposite side of $R_1H_1$ as compared to $O$ .

There are $19$ defined points on $TR_1$ (excluding $T$ and $R_1$ ) which are connected to $O$ by line segments such that $TR_1$ is on opppsite side of $O$ as compared to $JH_1$ .

There are $19$ defined points on $JH_1$ (excluding $J$ and $H_1$ ) which are connected to $O$ by line segments such that $TR_1$ is on opppsite side of $O$ as compared to $JH_1$ .

Please zoom in if the image is small to see.

The answer is 1304.

1 solution

Ashish Menon
Apr 2, 2016

In triangle $VTJ$ , there are $210$ triangles. Similarly, $R_1H_1S_1 , R_1OH_1, JOH_1,JOT, TOR_1$ have $210$ triangles.

Now, in triangle in $OR_1S_1$ , there $10$ triangles. In this counting I have excluded the individual triangles which I counted in previous procedure.
Now, we see that $OS_1H_1 , VJO , VTO$ are exactly the same like $OR_1S_1$ , so each of them have $10$ triangles .

Now in square $TR_1H_1J$ , there are $4$ triangles namely, $TJR_1 , TJH_1 , TR_1J , JH_1R_1$ .

So, the total number of triangles are $(210 × 6) + (10 × 4) + 4 = \boxed{1304}$ triangles.

Why is it 310? Am I missing something? If it needs to be non-degenerate it should include V, so there would be $\binom{21}{2}=210$ ways of getting triangles from the remaining points.

Vishnu Bhagyanath - 5 years, 2 months ago

@Ashish Siva

Vishnu Bhagyanath - 5 years, 2 months ago

Nothing wrong, its my bad, I will get ir fixed, thank you :-). I took 310 instead of 210

Ashish Menon - 5 years, 2 months ago

@Ashish Menon – It's been much longer than 15 minutes, care to explain why it is 310?

Vishnu Bhagyanath - 5 years, 2 months ago

@Vishnu Bhagyanath – Sorry again, I am wrong

Ashish Menon - 5 years, 2 months ago

@Ashish Menon – I initially intended something else

Ashish Menon - 5 years, 2 months ago

thank you sir

Rohit Nandwani - 1 year, 3 months ago

Strange hexagon

The answer is 1304.

1 solution

0 pending reports