Stretch

A soap bubble stretches between two identical unit rings (with radius 1).
What is the maximum separation between the two rings before the bubble pops?
The answer is 1.325486.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Amazing solution
by calculus of variations you mean treat the integrand as a Lagrangian L ( x , y , y ′ ) ?
so we get ∂ y ∂ L = d x d ( ∂ y ′ ∂ L )
If the LHS is zero then I can follow your statement about the constant we get. Why is the derivative with respect to y equal to zero?
Thanks
Log in to reply
Yes. That is right. However, when L does not depend explicitly on x , a first integral of this equation is L − y ′ ∂ y ′ ∂ L = c o n s t . and that is the equation I am using.
Log in to reply
I need help.
∂ y ∂ L − d x d ∂ y ′ ∂ L L ′ y ′ 1 − ( ∂ y ′ ∂ L ) ′ L ′ − ( ∂ y ′ ∂ L ) ′ y ′ = 0 = 0 = 0
I'm not sure if I integrated both sides with respect to d x I'd get the the expression you use. What am I missing?
Log in to reply
@Uros Stojkovic – Given that ∂ y ∂ L − d x d ( ∂ y ′ ∂ L ) = 0 we see that d x d ( y ′ ∂ y ′ ∂ L ) = y ′ ′ ∂ y ′ ∂ L + y ′ d x d ( ∂ y ′ ∂ L ) = y ′ ′ ∂ y ′ ∂ L + y ′ ∂ y ∂ L = d x d L − ∂ x ∂ L and so, if L does not depend explicitly on x , we have d x d ( L − y ′ ∂ y ′ ∂ L ) = 0 as required.
Log in to reply
@Mark Hennings – I didn't know about the fact that derivative of a function f ( x , y 1 ( x ) , y 2 ( x ) , ⋯ , y n ( x ) ) can be expressed as:
d x d f = ∂ x ∂ f + ∂ y 1 ∂ f y 1 ′ + ∂ y 2 ∂ f y 2 ′ + ⋯ + ∂ y n ∂ f y n ′
It nicely combines concept of total derivative and chain rule. Thanks for explanation.
I got as far as working out the surface was a catenary of revolution. I then thought it should be solved for when the waist point went to zero - wrong. Awesome solution.
Mathematically understood, btw, can u explain it in a manner of physics? THX
Log in to reply
Surface tension in the soap film will create a surface of minimum area.
Log in to reply
Thanks, but that's not what I would like to ask. What really bothers me is the behavior of the surface once the distance is beyond the maximum. In other word, I want to know, how the bubble breaks in detail.
Log in to reply
@Yuan Xue – It's complicated,and I am not sure I can fully answer your question - I am a mathematician, not a physicist.
Approaching the critical value of L , the area of the stable catenoid is greater than that of two disks (one on each ring). At the point of collapse, the soap film appears to transition first to the unstable catenoid shape, and to then collapse to the two disk state. Try this .
Log in to reply
@Mark Hennings – Thanks a lot, the article really helps.
The soap film will be a surface of revolution such that y ( − 2 1 L ) = y ( 2 1 L ) = 1 and such that the surface area ∫ − 2 1 L 2 1 L 2 π y 1 + ( y ′ ) 2 d x is minimized. Standard Calculus of Variations arguments tell us that 1 + ( y ′ ) 2 y is constant. Solving the equation a 2 ( 1 + ( y ′ ) 2 ) = y 2 we obtain y = a cosh ( a x + u )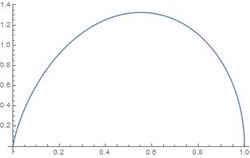 for some constant
u
. Since
y
(
−
2
1
L
)
=
y
(
2
1
L
)
=
1
we deduce that
u
=
0
and that
y
(
x
)
=
a
cosh
(
a
x
)
where
1
=
a
cosh
(
2
a
L
)
, and hence
L
=
2
a
cosh
−
1
a
−
1
0
<
a
<
1
Plotting the graph of
y
=
2
x
cosh
−
1
x
−
1
, we solve numerically to find that the maximum value of
L
is
1
.
3
2
5
4
9
, achieved when
a
=
0
.
5
5
2
4
3
4
. Note that, for smaller values of
L
, there are two different values of
a
, and therefore two different surfaces that satisfy the equation. It turns out that the "small
a
" solution is an unstable minimum.
for some constant
u
. Since
y
(
−
2
1
L
)
=
y
(
2
1
L
)
=
1
we deduce that
u
=
0
and that
y
(
x
)
=
a
cosh
(
a
x
)
where
1
=
a
cosh
(
2
a
L
)
, and hence
L
=
2
a
cosh
−
1
a
−
1
0
<
a
<
1
Plotting the graph of
y
=
2
x
cosh
−
1
x
−
1
, we solve numerically to find that the maximum value of
L
is
1
.
3
2
5
4
9
, achieved when
a
=
0
.
5
5
2
4
3
4
. Note that, for smaller values of
L
, there are two different values of
a
, and therefore two different surfaces that satisfy the equation. It turns out that the "small
a
" solution is an unstable minimum.