Strike a chord
Consider concentric circles with respective radii
π
and
2
π
. Choose two points on the larger circle independently and uniformly at random, and then join them to form a chord. If
P
is the probability that this chord intersects the smaller circle at at least one point, then find
⌊
1
0
0
0
P
⌋
.
Notation:
⌊
⋅
⌋
denotes the
floor function
.
The answer is 333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
It's very good that you specify exactly how you draw the random chord, as otherwise you fall to Bertrand's paradox .
Log in to reply
Yes, I had that paradox in mind when specifying how the chord was constructed. :)
If two points are chosen randomly and independently form the area of circular ring.Then what will be the probability that the line joining two points will intersect or touch the smaller circle.
Log in to reply
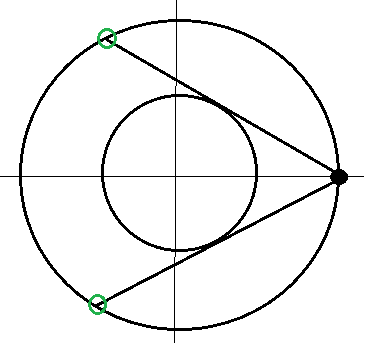
Yes, looking at the picture that has been added, (not by me), which is not actually an accurate reflection of the problem, the follow-up problem you suggest did occur to me as well. This will be a much harder problem. I would condition the distance of the first point from the origin, then with respect to the second point I would condition the length of the chords passing through the first point as a function of the polar angle. So we might be looking at a double integral, but I'll have to think about this some more to see if there is an easier approach.
P.S.. Do you think I should ask to have the diagram (and its caption) changed? It is a bit misleading.
Log in to reply
When I first saw the diagram then I thought the problem is this but later I read the question again then I got it.
Log in to reply
@Kushal Bose – Ok, I better ask for the diagram to be adjusted, then.
@Calvin Lin Sorry to bother you, but while I'm grateful that a diagram has been added to my problem, it is not an entirely accurate depiction of it, (although as Kushal and I have noted it might lead to an interesting follow-up problem). Would you be able to change it so that the line is actually a chord of the larger circle, and perhaps also eliminate the caption? Thanks in advance. :)
Log in to reply
@Brian Charlesworth – How's the picture now?
Log in to reply
@Calvin Lin – Looks great. Thanks for making the change. :)
Easily you can realise that a circle inscribed in a equilateral triangle inscribed in another circle has a ratio of radius of 1 to 2. Since the inscribed equilateral triangle separates the circle into 3 equal arcs, the probability is 1/3
 Not perfectly drawn
Not perfectly drawn
Use trigonometry to calculate the greatest angle ( A ) at which a c h o r d - whose 1st point starts at the base of a centre line - will intersect the smaller circle, relative to the centre. I.e. 2 π is the hypotenuse, and π is the opposite edge of the angle we are looking for (which represents the intersecting range for one half of the circles).
2 π π = 0 . 5 = sin A
A = 3 0
There are 90 degrees of possibilities, in either direction, for a potential position of the 2nd point on the circumference of the larger circle, ranging from the top of the centre line to a position that is infinitely close to the 1st point (at the base of the centre line).
As both halves of both circles have the same proportions, we don't need to unnecessarily extend the calculation for the probability ( P ) for this problem beyond 90 degrees. Both sides are equivalent, and we already have the intersecting range that would apply to the other half (30 degrees).
P = 9 0 3 0 = 3 1
The greatest integer equal to or less than 1 0 0 0 P
⌊ 3 1 0 0 0 ⌋ = 3 3 3
Actually, there's no need for trigonometry. It's obvious that it's a half of an equilateral triangle.
Log in to reply
Why is it obvious?
Log in to reply
Suppose a random point A on the larger circle and then draw a line that is tangent to a smaller circle in a point B. Name the origin of the circles C. Because the angle ABC is right and AC (e.g. the hypotenuse) is two times as long as AB, it follows that the triandle ABC is a symmetric half of an equilateral triangle - the angle BAC is therefore 30 degrees. Not saying that there was anything wrong with your approach.
Log in to reply
@Scrub Lord – This was actually my solution. I do normally prefer to use the bare minimum to solve a given problem. But this approach works equally well when applied to concentric circles of varying ratios (it just wasn't necessary).
Nice explanation, though. You should have written a solution, so that others can learn from it.
Why is 1/3 not multiplied by 2?
Log in to reply
Oh, I missed this comment. Sorry about that.
I assume that you're asking this because I've only calculated the angle (30 degrees) for half of the circle.
If 60 degrees is the total intersecting range for both halves, 180 degrees is the potential range for the 2nd point.
60/180 = 1/3
We don't need to multiply by 2 because the proportion for half the problem is the same as the proportion for the entire problem.
Is 1/3 not the probability of the angle being witgin the 30 degrees and thus in the smaller circle? So 2/3 is the actual probability (60/90, since the angle can be greater than 30 degrees but not less), right? Can you tell me what I did wrong?
Log in to reply
In this problem, we're looking to find the probability that a chord will intersect the smaller circle, which is every angle within A (labelled on my diagram).
2/3 (60/90) is the probability that the chord won't intersect the smaller circle.
Choosing a random angle at point A is not the same as choosing a random point on the circumference. At least, it is not obvious that they lead to the same range of probabilities. On the other hand, a bit of investigation does give a (to me) surprising result.
I can see that choosing a point B on the right hand half of the circumference of the larger circle is the equivalent of choosing an angle between 0 and 180 degrees representing the angle ACB (where C is the centre of the circle). Call this angle X. The method shown above chooses an angle at point A between the horizontal axis and the chord AB. Call this angle Y. As Y goes from 0 to 90 degrees, X goes from 0 to 180 degrees. The two methods of selecting a point would only produce an equal 'spread' of possibilities if X/180 = Y/90 for every angle Y. That is, X=2Y for every Y.
However the internal angles of the isosceles triangle ACB are (90 - Y), (90-Y) and X which must sum to 180. Hence 2(90 - Y) + X = 180 which solves to X = 2Y. Therefore the above method of selecting a random point (by choosing a random angle at A) is indeed equivalent to selecting a random point on the half-circumference. My apologies for doubting it.
The region of interest is the one between the green points in the diagram. First, find out the slopes of the tangent lines which intersect the smaller circle. Equation of a tangent line is below:
y = m ( x − 2 π )
The equation of the lesser circle is:
x 2 + y 2 = π 2
Plug the first equation into the second:
x 2 + m 2 ( x 2 − 4 π x + 4 π 2 ) = π 2 x 2 ( 1 + m 2 ) + x ( − 4 π m 2 ) + 4 π 2 m 2 − π 2 = 0
This is a quadratic equation in x, for which there are generally two solutions. However, we are particularly interested in the case in which there is only one solution. Use the usual ( b 2 − 4 a c = 0 ) trick to get:
1 6 π 2 m 4 − 4 ( 1 + m 2 ) ( 4 π 2 m 2 − π 2 ) = 0
Solving this equation yields m = ± 3 1 . Now we need to see where this line intersects the larger circle. Plugging the m value into the equation for the larger circle gives:
x 2 + 3 1 ( x − 2 π ) 2 = 4 π 2
Solving this equation yields x = − π . By inspection, when the x coordinate has a value of − 2 R , this corresponds to θ = ± 1 2 0 ∘ . There is an angular separation of 120 degrees between these two angles, meaning that the region of interest occupies exactly one third of the entire angular space.
⌊ 1 0 0 0 / 3 ⌋ = 3 3 3
Nice solution. Thanks for posting it. I had started working on my solution before you had posted yours, but we've taken different approaches so I'll leave mine up as duplication is not an issue.
Log in to reply
Yeah, yours is quite simple. I like it. I tend to lean very heavily on the "analytic geometry" side of things, but there's often a simpler way. By the way, are you going to re-post that rope / hole problem?
Log in to reply
Thanks. It will be interesting to see if someone can come up with yet another approach. As for the rope question, I'm hoping to get it reposted some time. I had to delete it as I had been working with different scenarios and got my numbers crossed up, which Mark Hennings pointed out to me. He used a different DE than I did, so I first want to make sure that our two methods yield the same answer for the next data set I come up with.
Log in to reply
@Brian Charlesworth – I have submitted an approach that is different. The answer I got was correct, but the simplicity of my approach (compared to the other solutions) has me wondering whether I just got the correct answer by accident, and have fallen foul to a principle that I'm not aware of.
Log in to reply
@Jonathan Quarrie – No "fouls"; your solution looks good. :) You've taken roughly the same approach as I did, the difference being that you look at the angle A at the point on the larger circle and I look at the angle at the center.
Did the same :))
Similar to @Steven Chase 's solution:
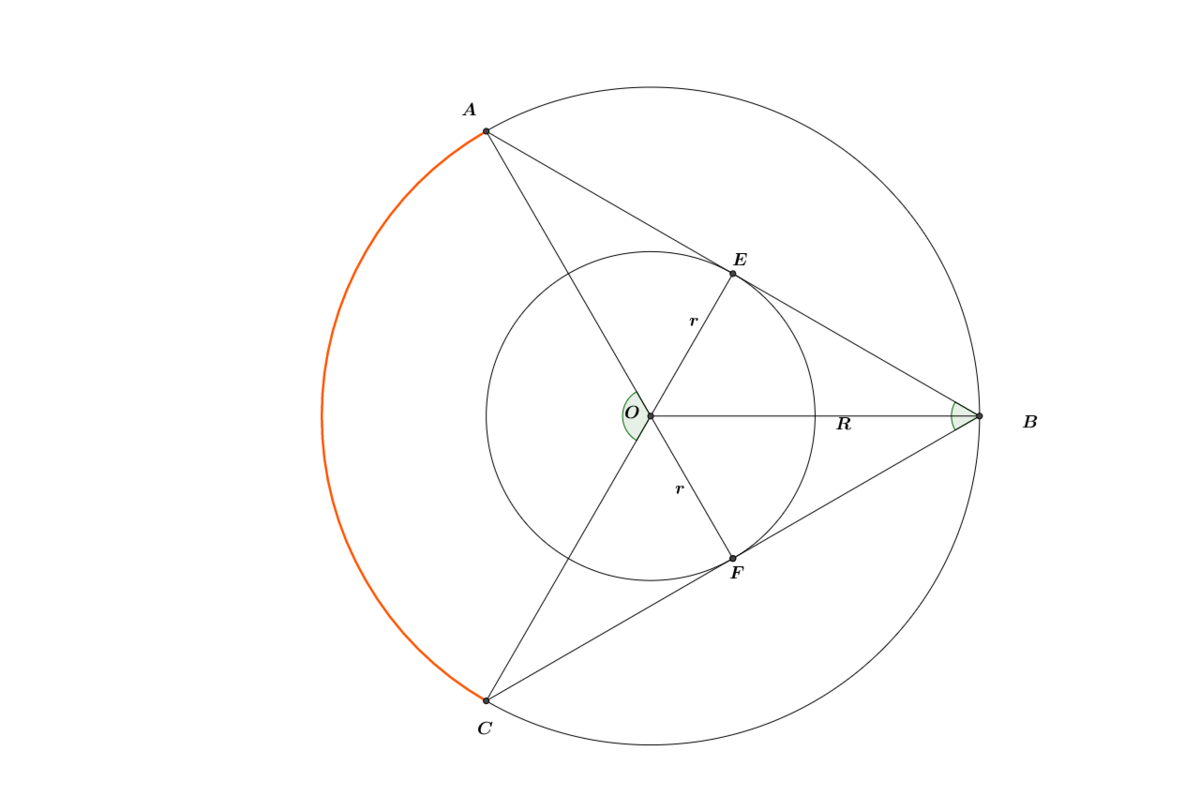
Let the 2 circles be centered at O . Once the first point B is chosen, the second point has to lie in the minor arc A C for the chord to intersect the small circle.The probability of the point lying on the arc is given by,
P = Perimeter of the large circle Length of minor arc AC = R ⋅ 2 π R ( ∠ A O C ) = 2 π ∠ A O C
Consider the Δ O E B right angled at E
∠ O B E = sin − 1 R r
by symmetry we have,
∠ A B C = ∠ E B F = 2 ∠ O B E ∠ A B C = 2 sin − 1 R r ∠ A O C = 2 ∠ A B C Angle subtended by an arc at the center is double the angle subtended by it on any other point on the circle ∠ A O C = 4 sin − 1 R r
thus the required probability is,
P = 2 π 4 sin − 1 R r
In the given problem r = π and R = 2 π , thus R r = 2 π π = 2 1
P = 2 π 4 sin − 1 2 1 = 3 1 ⌊ 1 0 0 0 P ⌋ = 3 3 3
Let
A
and
Z
be the points picked. Rotate the figure so that
A
is at the top.
Z
remains uniformly distributed around the circle.
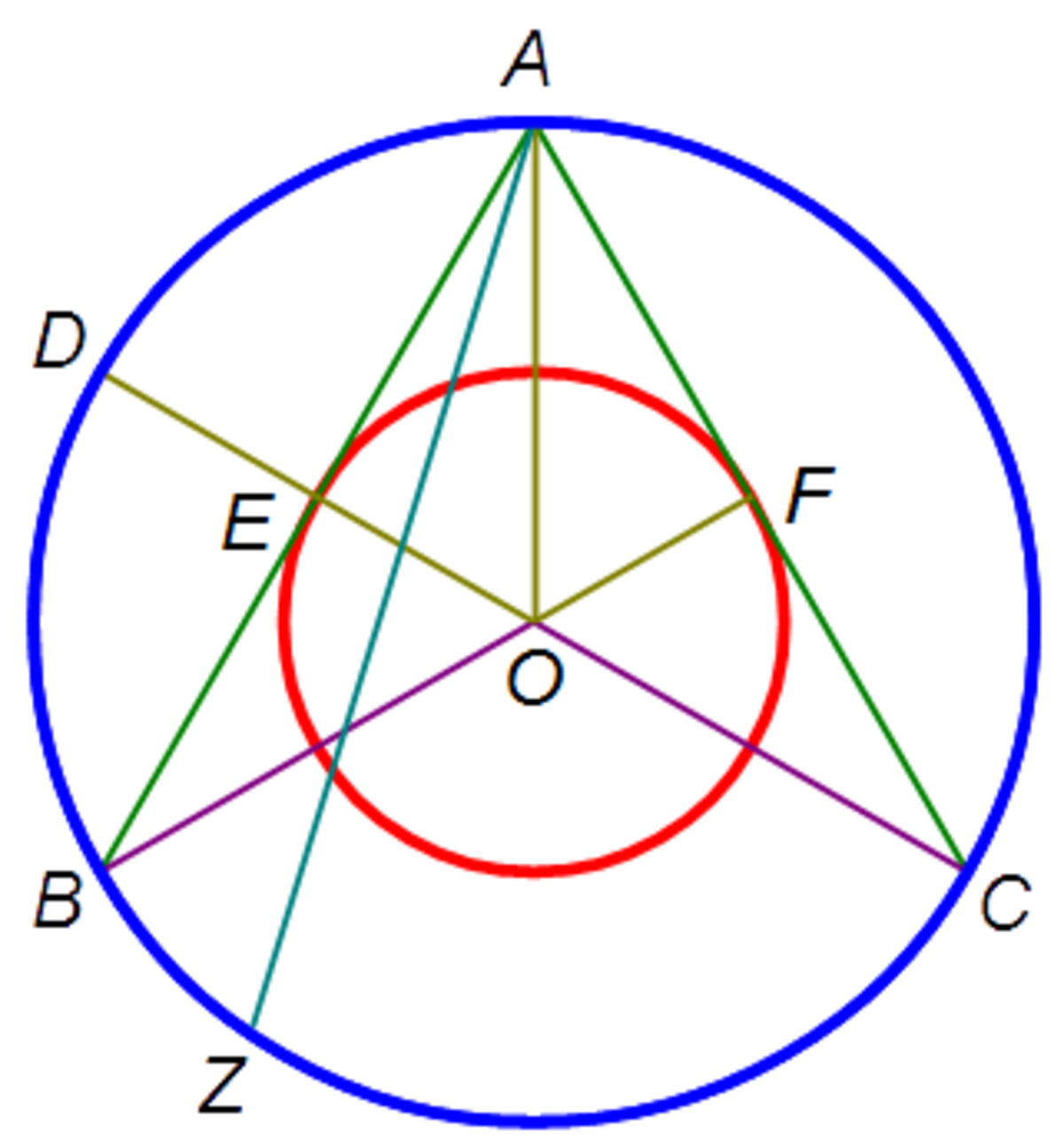
Let A B be a chord that is tangent to the inner circle. Draw the diameter C D through the point of tangency E . Obviously C E = 3 π and E D = π . By the intersecting chord theorem, A E = 3 π , therefore A E O is a 90-60-30 triangle. So is A F O by the same argument. Therefore ∠ B A C = 6 0 ∘ , hence ∠ B O C = 1 2 0 ∘ .
A Z intersects the inner circle whenever Z is on the minor arc B C . Since ∠ B O C = 1 2 0 ∘ , this is 3 1 of the circle, therefore P = 3 1 .
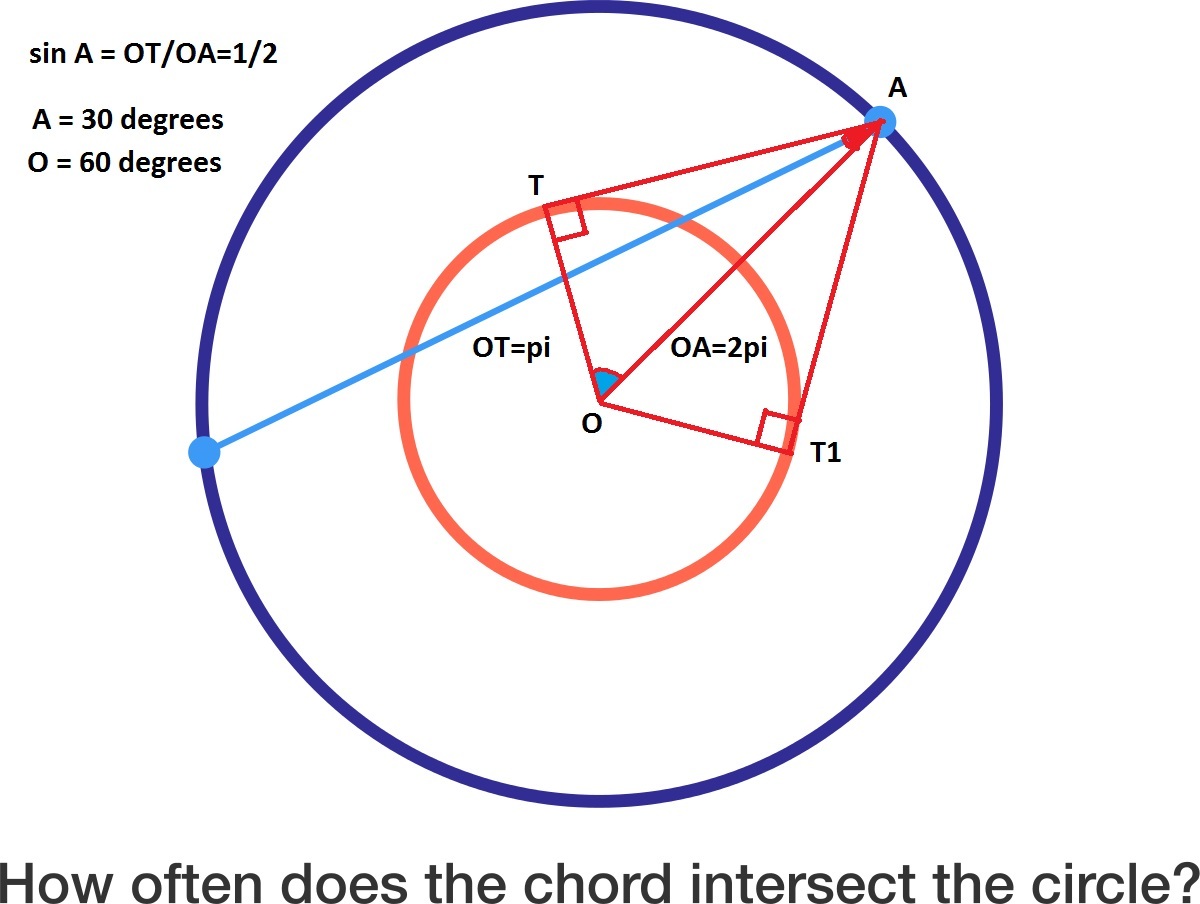
I used 2-dimensional geometric probability by angles. The central angle TOT1 is 120 degrees.
P=120/360=1/3
1000xP=1000/3
The answer is 333.
This was weird, because the solution came to me intuitively and I barely know how to justify it. It is based on the Euler-inequality, that states that for a triangle's circumradius R, and inradius r, R ≥ 2 r and it is equal if and only if it's an equilateral triangle. This last part was something that seemed really obvious, and it pops out when you actually take a random point on the outer circle and draw the equilateral triangle that touches the inner circle. Since this triangle divides the outer circle in three equal parts, all the lines that don't cross the triangle, and thus the second chosen point is covered by the triangle from the first one's viewpoint, are the ones that also intersect the circle. These are the points in one third of the outer circle, thus 1000*1/3 floored, 333.
Good intuition. Your explanation justifies it well. :)
The radii of the circles R and r do not matter much; only the ratio r / R = 1 / 2 is relevant here.
If both points are chosen uniformly on the circle, the arc distance θ between them will be uniformly distributed on [ 0 ∘ , 1 8 0 ∘ ] .
The chord between the points reaches it smallest distance to the center of the circle at its midpoint. The distance between that midpoint and the center of the circle is well-known to be d = R cos 2 θ . (For proof, connect the two points and the midpoint to the center of the circle, and analyze one of the two right triangles.)
We require d ≤ r , which means R cos 2 θ ≤ 2 R , cos 2 θ ≤ 2 1 , 2 θ ≥ 6 0 ∘ , θ ≥ 1 2 0 ∘ . Thus we find that θ ∈ [ 1 2 0 ∘ , 1 8 0 ∘ ] , which is one-third of the interval.
Conclusion: P = 1 / 3 and ⌊ 1 0 0 0 P ⌋ = 3 3 3 .
Points on the larger circle are uniquely definded by θ 1 , θ 2 ∈ [ 0 , 2 π ] , if the two circles are centered in O in the x y plane. Given the first point P 1 on the bigger circle, it's proven, with a bit of trigonometry, that the angle between the two lines passing from P 1 to the tangent points on the smaller circle is 3 π . Now, the two tangent lines also intersect the bigger circle, creating an arc 'containing' all the points P 2 that, if connected to P 1 , create chords that intersect the smaller circle. Due to the fact that the probability density function is 4 π 2 1 ( ∫ 0 2 π ∫ 0 2 π 4 π 2 1 d θ 1 d θ 2 = 1 ) and that the arc is 3 2 π (I omit the proof), the probability can be calculated as
P = ∫ 0 2 π ∫ 0 3 2 π 4 π 2 1 d θ 2 d θ 1 = 3 1 ≈ 0 . 3 3 3
Solution area angle must be between 0 and 60. Therefore the arc can be 2pi/3 of the circle; which is 1/3 ==> 0.3333... probability.
not so sure, depends on how we consider uniform random... may be also 0.5 if chord is differently chosen
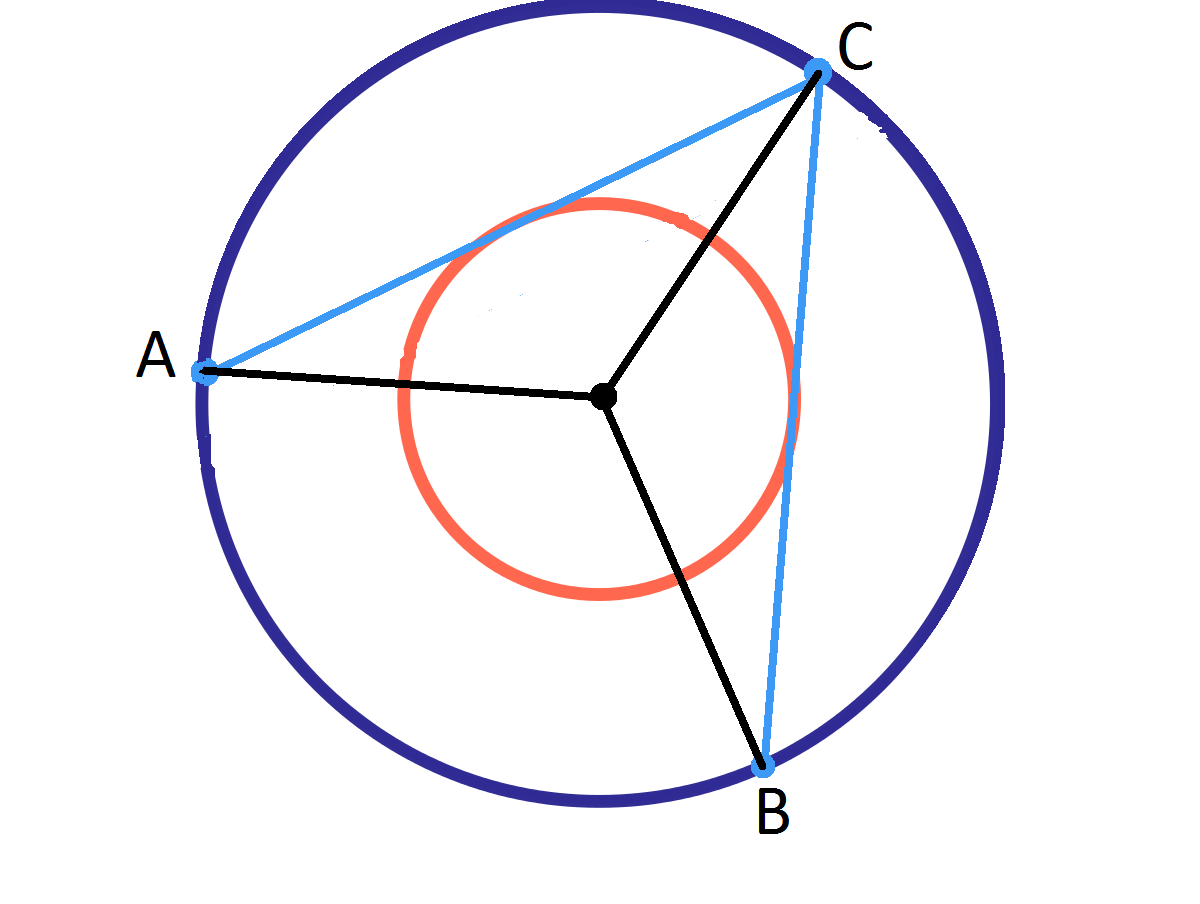 Call the first point A, 2nd point B, 3rd point C and the center D. The 2 random points formed in the outer circle of radius 2r form an angle in the interval [0, 360] with the center of the two circles. In order for the 2 points to cross the smaller circle of radius r, the second point must be between the 2 tangent lines between the inner circle and the first point. We can draw line AB and line AC. We know the line creates a right angle with the point of intersection, center and the first point. We see the hypotenuse is the bigger radius 2r and one of the legs is the smaller radius r. This is the ratio of a 30-60-90 triangle, therefore we know that the 2 angle formed is
6
0
⋅
2
and
6
0
⋅
4
, or
1
2
0
and
2
4
0
. This is an interval of size 120, therefore the probability is 120/360 or 1/3. multiplying by 1000 and taking the floor, we get
3
3
3
.
Call the first point A, 2nd point B, 3rd point C and the center D. The 2 random points formed in the outer circle of radius 2r form an angle in the interval [0, 360] with the center of the two circles. In order for the 2 points to cross the smaller circle of radius r, the second point must be between the 2 tangent lines between the inner circle and the first point. We can draw line AB and line AC. We know the line creates a right angle with the point of intersection, center and the first point. We see the hypotenuse is the bigger radius 2r and one of the legs is the smaller radius r. This is the ratio of a 30-60-90 triangle, therefore we know that the 2 angle formed is
6
0
⋅
2
and
6
0
⋅
4
, or
1
2
0
and
2
4
0
. This is an interval of size 120, therefore the probability is 120/360 or 1/3. multiplying by 1000 and taking the floor, we get
3
3
3
.
Suppose in general the two circles have radii k and 2 k . Center them both at the origin O . Now without loss of generality, once the first random point is chosen, we can rotate the larger circle so that this point sits at A ( 0 , 2 k ) . Now draw a chord A B (down and to the right) that is tangent to the smaller circle at P . Then Δ O P A is right-angled at P with hypotenuse length ∣ O A ∣ = 2 k and adjacent leg length ∣ O P ∣ = k . As cos ( ∠ A O P ) = 2 k k = 2 1 we see that ∠ A O P = 6 0 ∘ , and so by symmetry ∠ A O B = 1 2 0 ∘ .
Thus if the second point B is chosen so that ∠ A O P < 1 2 0 ∘ then the chord A B will not intersect the smaller circle, and if 1 2 0 ∘ ≤ ∠ A O P ≤ 1 8 0 ∘ the chord will intersect the smaller circle at at least one point. By symmetry the same result will occur if the chord is drawn down and to the left. In each case there is a 1 8 0 1 8 0 − 1 2 0 = 3 1 probability that the chord will not intersect the smaller circle, so since there is a one-to-one mapping between the random choice of B and ∠ A O B we can conclude that P = 3 1 , and that ⌊ 1 0 0 0 P ⌋ = 3 3 3 .