Stringent Numbers 2
Logic
Level
3
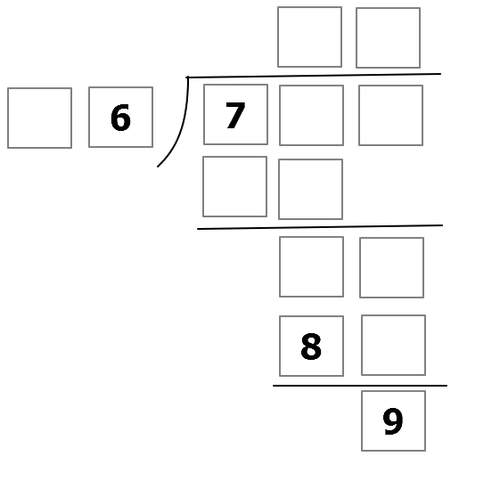The above shows a long division between 2 integers, with the last box at the bottom representing the remainder of the quotient. Each box represents a single digit non-negative integer.
What is the sum of all the missing numbers?
The answer is 48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The division is between the numbers 729 and 16, which has a quotient of 45 and a remainder of 9.
(? = unknown digits)
Since ?6 can't be 0, it can be 16, 26, 36, 46, 56, 66, 76, 86, or 96. However there is a part where in a number is multiplied to ?6 in order to form 8? . Only 16 has a multiple which satisfies 8? which is 16 x 5 = 80. Therefore 16 is the divisor.
Working Backwards, the last digit of the quotient is 5 because of the 8? (which is 80). Then, above it is 89 (since 80 + 9)[ the last digit of the dividend will be 9]. Then above it is 7? - ?? = 8, since the ?? should be a multiple of 16 and less than 7? it is 64 (7 x 4). So 7? - 64 = 8 , the ? there is 2.
So the Dividend: 729
the Divisor: 16
And the digits in the blank boxes are 1 + 4 + 5 +2 + 9 + 6 + 4 + 8 + 9 + 0 = 48
So the answer is 48.