Subway Surfers Fans, jump in now !
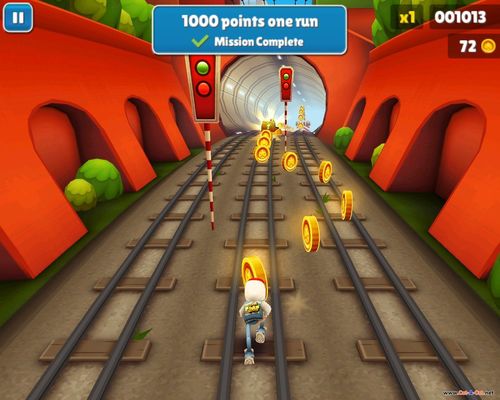 In the game
Subway Surfers
you have to collect coins in 3 lanes as seen in the picture. Let's call them as lanes A,B and C.
In the game
Subway Surfers
you have to collect coins in 3 lanes as seen in the picture. Let's call them as lanes A,B and C.
Because of the barriers in the way, he has to jump or roll to dodge a barrier.
In a particular run, the player jumped 100 times.
Then the number of jumps he made in the lanes A,B and C was J A , J B , J C respectively.
How many possibilities are there for the ordered triple ( J A , J B , J C ) ?
Details and assumptions :-
∙ It's possible that no jumps were made in some lane.
∙ The player makes an integer number of jumps in each lane.
∙ The number of jumps in any lane can't be negative obviously.
The answer is 5151.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Short, sweet, nice and beautiful,
Though not 'as-usual' colourful!
Subway Surfers, what an idea!,
Hats off, Adi bhaiya!!
You are awesome, thanks a lot
From you, gr8 inspiration I got
You're an ideal, so good an' wise
Come ter earth, b'fore me eyes.
Thas' why I write this line,
Dedicated to you, yo're divine!
How proud I am to be your fan,
You're more than awesome, man!
We're lucky to meet you here,
Shall we find sum1 so gr8 anywhere
B'fore Krishna Ar sees this, lemme tell you
you both're genius, I think this will do!
Log in to reply
Reminds me my old times when I too used to make poems .... This deserves the "All likes" pic I had made....
 i
i
and also,,,,
 img
img
How long did it take you to make this? :O
Log in to reply
@Sean Ty It took about 5 mins to bind,
When I wrote the 1st line, 2nd came in mind,
"bhaiya" is a word here, should you find,
That means 'big brother', sort of that kind!!
I'm very sure he just made this while writing.... All the rhyming was instantaneous, like while writing the line, next line comes to the mind.... Because that is what used to happen with me :P
Log in to reply
@Aditya Raut – Amazing. Same thing happens to me, except the words don't come instantly. Wow
@Aditya Raut why di you use three in the stars and bars formula .Shouldnt it be 2?
Log in to reply
It is 2, the number of groups is 3, I guess...
I had made it "100+3-1" which was simply "100+2", i made that by number of groups in stead of number of bars. Reaches same finally !
Same method, but a silly mistake while calculating. Used 102/2=56 and then fed up gave 2 random tries and then seeing the solution, got the mistake. Anyways, great question!
Simply use combinatorics with repetition let x 1 + x 2 + x 3 = 1 0 0 since x 1 , x 2 , x 3 , ≥ 0 , then we have C ( 1 0 0 + 3 − 1 , 1 0 0 ) = C ( 1 0 2 , 1 0 0 ) = 1 0 2 ! / ( 1 0 0 ! 2 ! ) = ( 1 0 2 × 1 0 1 ) / 2 = 5 1 5 1
Let us draw 1 0 0 stars which are for the jumps he made and let us have 2 bars for the number of lanes.We are considering only 2 bars because when we put these bars in between the stars we will have divided the 1 0 0 stars in 3 groups as desired.Now,if we have 1 0 0 stars then we can put the bars in 9 9 places.So,we have 9 9 places to put the bars in and 2 bars.Thus,we can divide the 1 0 0 stars in ( 2 9 9 ) ways.But by doing this we are not taking into account the cases which include 0 jumps in 1 or 2 lanes.Let us say that in two lanes there were 0 jumps.Thus,the cases are A , B , C = 0 , 0 , 1 0 0 ) ( 0 , 1 0 0 , 0 ) ( 1 0 0 , 0 , 0 ) . Now,let us say that he didn't jump in 1 lane.Thus,the sum of the jumps into other lanes is 1 0 0 . These cases are ( 0 ) , ( 1 , 2 , 3 , 4 . . . . . . 9 8 , 9 9 ) , ( 9 9 , 9 8 , 9 7 , 9 6 . . . . . . 1 ) ( 1 , 2 , 3 , 4 . . . . . . 9 9 , 9 9 ) , ( 0 ) , ( 9 9 , 9 8 , 9 7 , 9 6 . . . . . . 1 ) ( 9 9 , 9 8 , 9 7 . . . . 1 ) , ( 1 , 2 , 3 . . . . . . . . . . . . 9 9 ) , ( 0 ) . The total is 9 9 ∗ 4 9 + 3 + 9 9 ∗ 3 = 5 1 5 1 .
Stars and bars method. I studied beggars and coins method, a similar one.
Use a Generating Function
Mathematica:
Coefficient[Sum[x^i, {i, 0, 100}]^3, x, 100]
Okay, nice thinking way. This has simpler "non-computer" solution too this time though :P
Log in to reply
A harder question is How many possibilities are there for the unordered set {J A, J B, J_C}?
Just have to find the no. of non negative integral solutions of a+b+c=100 that is (100+3-1)C(3-1)=102C2=5151
Yes thats the method, but same method posted above has >10 upvotes and this one 0
We want the ordered triples whose sum is 1 0 0 .
100 stars, 2 bars, bars could be adjacent
(2 bars will divide in 3 groups, the 3 numbers)
According to the Stars and Bars Formula for ' n ' stars and ' k ' bars, you have to choose n places for the stars, which is same as choosing k places for bars, from the total n + k places available. Simply ( k n + k )
We get that the required number will be
( 2 1 0 0 + 2 ) = ( 2 1 0 2 ) = 2 1 0 1 × 1 0 2 = 1 0 1 × 5 1 = 5 1 5 1