Sufficiently Distinct?

Logic Level 1

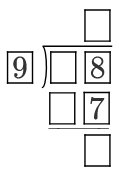
The above shows an incomplete long division. Which of the following digits was not used in this division?

1 2 3 4

1 solution

A Former Brilliant Member
Aug 9, 2016

Relevant wiki: Arithmetic Puzzles - Fill in the Blanks

$\LARGE{ \begin{array}{rll} \phantom{0}\ \boxed{{3}} && \\[-2pt] \boxed{{9}}\ \enclose{longdiv}{\boxed{{2}} \ \boxed{8}}\kern-.2ex \\[-2pt] \underline{\boxed{{2}} \ \boxed{7}} && \\[-2pt] \boxed{{1}} \end{array} }$

Steps: We know that any number multiplied by 9 should give 7(as last number).Only one possiblities satisfy i.e. 3.
This gives $9×\boxed{3}=\boxed{2}7$ .

Now we need to find divident.We know that a single number from 1-9 will be filled in the box.But only possibility is 2.Because if we will any number greater than 2 reminder will be of two digit and that is not possible according to question. :)

Therefore, the only number which is not used from the given options is $\boxed{4}$ .

Moderator note:

Can you show how you complete the long division? Is the solution unique? Why or why not?

To- Challenge Master note: We know that any number multiplied by 9 should give 7(as last number).Only one possiblities satisfy i.e. 3.
This gives $9×\boxed{3}=\boxed{2}7$ .

A Former Brilliant Member - 4 years, 10 months ago

Right! You should add that to your solution =D =D