Sum of angles??
What is the sum of angles in degrees of the orange colored angles in the given figure?
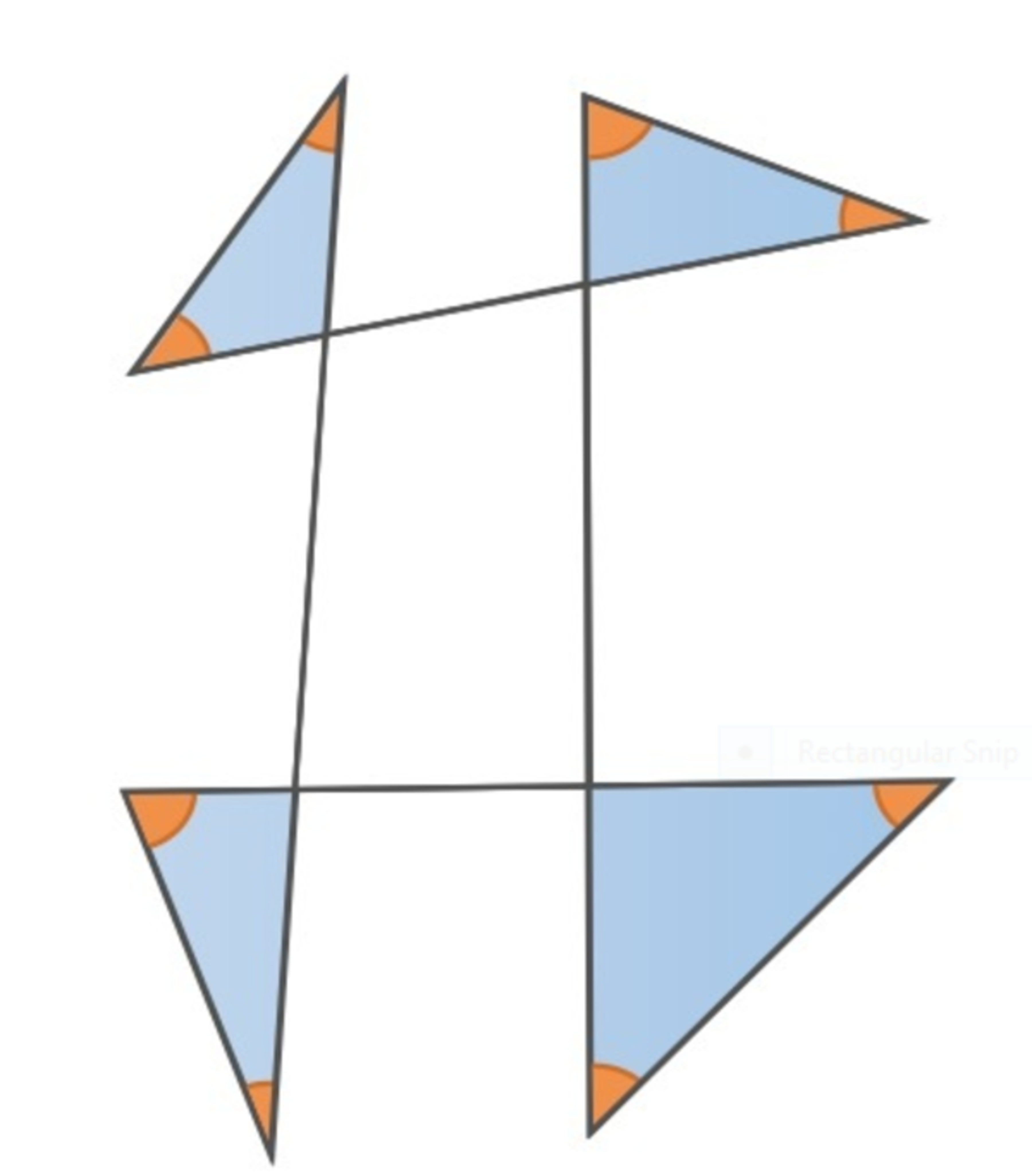
The answer is 360.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If you walked all the way along this path back to your starting point, you would have turned round exactly once.
Log in to reply
Chris, l didn’t get your point.
Log in to reply
It's just another way of showing the angles sum to 3 6 0 ∘ . Every time you turn while following the path, you turn in the same direction, so the "total turn" is the sum of the orange angles. But you end up facing the same direction you started in.
Log in to reply
@Chris Lewis – Thank you for the clarification. I agree with your analysis.
EDIT : Acknowledging @Steven Adler 's comment that the central figure in this problem is not a parallelogram but rather, a quadrilateral. This is to avoid confusion from anyone. Forgive me for late edit in the explanation.
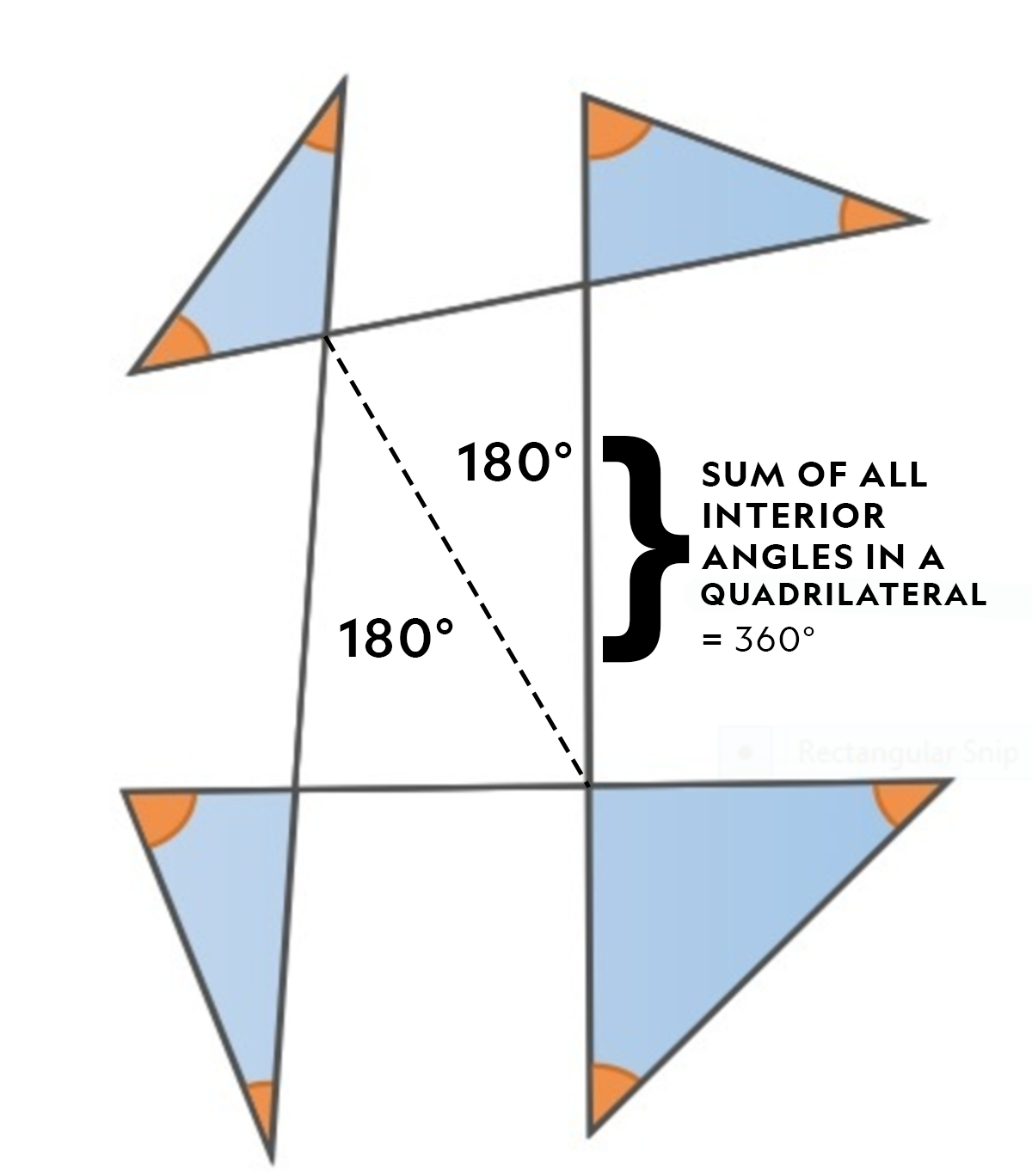
We know that the sum of all interior angles of any quadrilateral amounts to 3 6 0 ∘ . So, what I did in my solution was to cut down the quadrilateral into two triangles for simplicity's sake. We then know that all triangles have interior angles summing up to 1 8 0 ∘ . We can now use this information to find the sum of all angles colored orange from the figure above.
Let's also take the fact that vertically opposite angles are equal. This means that each o r a n g e indicated angles of the outer triangles equals the b l u e angles (or corners) of the quadrilateral divided into two triangles as shown below.
So, the sum of given angles will be:
( 2 × 1 8 0 ∘ ) + ( 2 × 1 8 0 ∘ ) − 3 6 0 ∘ = 3 6 0 ∘
The sum of the interior angles of ANY quadrilateral, not just parallelograms, is 360. There is no indication that the figure in the problem is in fact a parallelogram.
Log in to reply
Hmmm... I was inclined to believe that every quadrilateral is a parallelogram. But may you please differentiate exactly the difference between a quadrilateral and that of a parallelogram?
Log in to reply
No, parallelograms have opposite sides parallel, and therefore equal. All rectangles and rhombi, and therefore all squares, are parallelograms. But not all parallelograms are rectangles (if they have angles not equal to 90) or rhombi (if all 4 sides are not equal length). Quadrilaterals which are not parallelograms include trapezoids, irregular quadrilaterals, concave quadrilaterals (including darts), and convex kites which are not rhombi. A quadrilateral is any 4 sided polygon.
Log in to reply
@Steven Adler – Oh yes. I forgot about figures like trapezoids that at least one pair of lines, if extended, intersect each other. Thank you for the clarification sir. It's always the best to refresh these concepts daily. :D
Log in to reply
@John Bryan Galiza – You are quite welcome. There is a nice Venn diagram on the web if you Google types of quadrilaterals. All squares are kites, and all darts are kites, but no squares are darts!
@John Bryan Galiza , thank you for sharing your solution.
The sum is 360 degrees for ANY polygon with a triangle at each vertex.
For any N-gon:
There are N surrounding triangles.
Sum of all triangle angles is 180N
Subtract sum of all interior angles of N-gon, 180(N-2). These are the vertical angles subtracted from each surrounding triangle.
180N - 180(N-2) = 180N - 180N + 180x2 = 360
QED
Thank you for sharing your solution.
You are welcome.
Consider a regular 180-gon. Almost a circle. Each triangle around it is a (very) obtuse isosceles triangle with angles of 178, 1 and 1 degree. Total of angles in question is 180x2x1 = 360 degrees. Total of the interior angles of the regular 180-gon is 178x180 = 32,040 degrees. This is 180(180-2).
Sum of angles:
4 × 1 8 0 ∘ − 3 6 0 ∘ = 7 2 0 ∘ − 3 6 0 ∘ = 3 6 0 ∘ ,
Keep in mind that sum of angles in a quadrilateral is A + B + C + D = 3 6 0 ∘ and sum of angles in a triangle is 1 8 0 ∘