Sum of Gaps 2
Given that π = 4 k = 1 ∑ ∞ 2 k − 1 ( − 1 ) k + 1 , what is the value of
n = 1 ∑ ∞ ( π − 4 k = 1 ∑ n 2 k − 1 ( − 1 ) k + 1 ) ?
The answer is -0.5708.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
What are you using to pass from sumation to integral on the second step?
Log in to reply
I am just integrating the first identity from 0 to 1 , and then reordering terms.
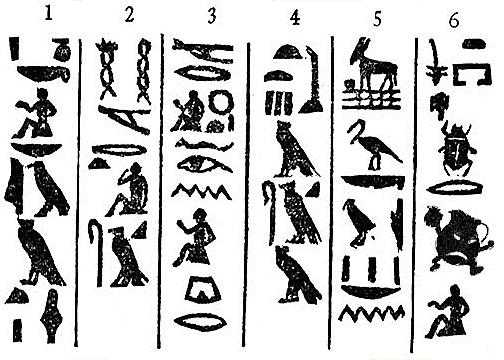
Mark, if you don't mind my asking, but what does that cartouche say? The best I can decipher its meaning is "Mark [...] of many books" I've asked an Egyptologist about this, who assumes that it's meant to be read phonetically, not semantically. He says that the best he can come up with is "Meretanure", but I have my doubts if that's what you intended for it to mean. I'm really puzzled with the inclusion of that pot in the middle.
Log in to reply
It reads (i)m(y)-r Tnw - "he who is in charge of numbers" - the nearest I can come up with as an epithet for "mathematician". The phonetic reading was correct (the "pot" can be read, inter alia, as "nw"). The Egyptians were prepared to overlook spelling in favour of aesthetics, and were willing to double letters (particularly to reinforce a disyllable like "nw").
If you read the symbols in order, they spell out: m- r - T - nw - n - w followed by triple strokes indicating a plural, and a papyrus roll indicating an abstract concept (in this case, a number). The letter "T" represents a "tj" sound.
The m-r pattern ("he who is in charge of") at the front is a standard abbreviation describing an official's role ("he who is in charge of the king's seal", "he who is in charge of the double granaries") frequently found on funerary inscriptions.
You can read the epithet (it is not a cartouche, which is the surrounding circle that encloses a pharoah's name) as
"imy r tjenu"
As you might guess, I have spent a little time learning to read Middle Egyptian. You are never alone in a museum if you are translating inscriptions - someone is bound to come and ask you what they say! There was the time the security guard in the museum in Geneva wanted to know (in French) (a) what I was doing going behind the statues - to read the inscriptions - and then (b) what they said.
Log in to reply
Correct, technically it's not a cartouche, since it doesn't have that border, otherwise it's arranged just like one. Nevertheless, it's a bit puzzling to read it either way, and as you have just said, "Egyptians were willing to overlook spelling in favor of aesthetics". Context becomes everything. I'll forward your comments about this to the Egyptologist that I've asked about this and see what he has to say about this.
What makes this difficult is determining which parts are to be read phonetically and which are to be read in logogrammic form. So, that pot was meant to be read phonetically as "nw" after all. That means you weren't trying to say "Mark", which would have needed a different "pot" for that, so to speak.
But you have co-authored a number of books, haven't you?
Log in to reply
@Michael Mendrin – The word "Tnw" is capable of many different spellings, with a number of possible extra symbols being added for dramatic/semantic effect. The spelling I have used is one of those listed in Raymond Faulkner's delightful handwritten(!) dictionary of Middle Egyptian (about the only resource available unless you have access to 19th Century German dictionaries, at least if you are looking for paper copy).
Log in to reply
@Mark Hennings – well, I'm hardlly an expert on this, but this Egyptologist I know loves this kind of stuff, so let me pass it on to him.
Log in to reply
@Michael Mendrin – Definitely that cartouche..."ahem"... hieroglyphic moniker, is pretty distinctive. It looks like some kind of imprimatur stamp.
@Michael Mendrin – Determining what is syllabic, what is determinative, what is logogrammic and (even) what is simply an Egyptian pun is part of the fun! Inscriptions on stone are particularly cryptic, since the engravers had space as a premium, and took all sorts of spelling/abbreviating/punning liberties. Add to that the fact that there are no vowels anywhere (like pre-diaspora Hebrew), and no punctuation, and you get the idea!
Books - now there's a change of subject. I have coauthored two graduate level books and, more recently, soloed a school-level Mathematics textbook.
Log in to reply
@Mark Hennings – well, there you go... I had assumed that hieroglyphic for a roll-tied papyrus combined with the strokes for "many" was intended to mean "many books" semantically, but, unfortunately, that combination also appears in many places as part of words, so I was left in the dark about that. But, so, here, you intended to refer to "many numbers" instead of "many books", and that pot symbol does semantically have the meaning related to "creation", i.e., loosely speaking, if I may, "He who is a cook of many numbers". Although, the meaning is supposed to be closer to a maker of pottery.
Log in to reply
@Michael Mendrin – There you start to see the game. The pot "nw" appears in the spelling of Nut, the Egyptian goddess of the sky. Nut is part of the creation process. Can that give the letters "nw" the meaning of creation...? I don't think so, in this case: "nw" is used pretty consistently in a syllabic manner. Your Egyptologist might have a different view.
Log in to reply
@Mark Hennings – Give me some time to get his opinion. But in the Gardiner list of hieroglyphics, that pot, designated as W24, does have the semantical meaning, "to construct, mold". I'll ask him again about this. What complicates things is that ancient Egyptian language is hardly static throughout its dynastic eras. At least within each era, there are certain stylistic norms, so that meaning and context can thereby be more accurately inferred. How much of the hieroglyphics is meant to be strictly read in syllabic manner, varies, but generally with the passing dynasties, even more so. I'm sure we probably can make a math problem out of this as to why this tends to be. Do you know of any ideogrammic language that "went backwards" to more pictorial form? ..uh... yeah, there is, emoticons. We have emoticons today.
Log in to reply
@Michael Mendrin – I am a little out of practice, it seems. The "nw" pot is more fluid that I indicated. It is a determinative (a non-syllabic, non-logogrammic symbol indicating a word-type) representing building, so it used with words like "qd" (to build, or fashion .. pots). It can then also be used as a pun (it is the determinative for "qd", so can be used to represent the sound "qd" as well) - it is used in the spelling for "qdd" to sleep.It also appears in some spellings of words, where it was used to replace other, similar, small round glyphs (for aesthetic reasons, maybe).
Surrounded as it was, in my avatar, by "n" and "w" symbols, the reading of W24 there was clear.
@Michael Mendrin – Certainly Egyptian evolved over the centuries, but there was a long time when Middle Egyptian was the standard, at least in formal writing. Also, don't forget that, in parallel to the hieoglyphic writings, Egyptian was written in hieratic too. This was the way the language was written on papyri, and is a much more cursive form of the script. Since there is more room on a piece of papyrus, there is more space for fuller spelling forms, so the syllabic nature of the language is more evident. It is wrong to think of Egyptian writing as fundamentally pictorial/ideogrammatic - it is a syllabic writing, with ideogrammatic aids.
Log in to reply
@Mark Hennings – Yes, I will assume you're going with the Middle Egyptian standard, which was the first to be deciphered and is now the most well documented, its use spanning roughly after the end of the Old Kingdom towards the end of the New Kingdom. Your point about the existence of hieratic writing as distinct from the well known hieroglyphic form (the latter clearly more suitable for inscriptions which are more durable) is also well taken. Even so, use of English has varied quite a bit in just a couple centuries of America's existence, even though English had always been its primary language. But now I'm being way too pedantic. Give me a chance to re-digest all this.
"It is wrong to think of Egyptian writing as fundamentally pictorial/ideogrammatic - it is a syllabic writing, with ideogrammatic aids." is a good summary of this Middle Egyptian standard.
Log in to reply
@Michael Mendrin – As they didn’t say in Thebes: “ ir n.k hrw nfr”, or “have a nice day”.
Log in to reply
@Mark Hennings – oh that was pretty cool, Mark
@Mark Hennings – I have word back from that Egyptologist. His first reaction was kind of interesting... he says
"m wr haty f s-wa'b ma'-khrw w'b tw2=ti r khww m-kht f rdi.(t) 'shw . s"
with great heart his makes-clean justified purified from sins after he let read it
He, too, wasn't clear initially whether or not it's supposed to be a cartouche, which does change how it's read, namely if it's a cartouche, it's a name and is to be read largely syllabically, or if it's not a name but a phrase (or a title) instead, in which case the hieroglyphics may be used as characters of meaning, along with phonetics and determinatives. He agrees with your observation that
"It is wrong to think of Egyptian writing as fundamentally pictorial/ideogrammatic - it is a syllabic writing, with ideogrammatic aids."
Even so, he says, "Welcome to the complications of reading ancient Egyptian hieroglyphics!" and adds that it's extremely difficult to "compose new texts in hieroglyphs" accurately enough that we could definitely say would have been well understood by the ancient Egyptians. We simply do not know enough about the context and modes of the ancient past to do a very good job of that, even though we today can read and understand it fairly well. Kind of like what happens when one is able to listen to and understand foreign language well, but not be able to speak it fluently.
Nevertheless, given these limitations, he does agree with you that your hieroglyphic moniker can be interpreted as
"he who is in charge of numbers"
given that it's a modern composition subject to "variant meanings" possible, including this title.
As he said, "this has been a fun romp!"
Log in to reply
@Michael Mendrin – I did consult with an Egyptologist at Oxford, who told me that there was no contemporary word for mathematician - the nearest thing would simply be “sS”, or scribe. Since “Tnw” does seem to have a meaning of number related to censuses of cattle, he did agree that my usage was reasonable, with the same caveats about not being sure about the meaning as your Egyptologist...
When I type-set the epithet, there was no cartouche, but the Brilliant avatar thing has cropped it and put it in a circular frame, which looks a little like a cartouche, I guess.
Of course, many king’s names have meanings, and not just syllabic value. Ramesses (Ra bore him), Tutankhamen (image of the life of Amun), Hatshepsut ( foremost of the female officials), to name a few. Other parts of a king’s titulary are entirely meaning-based. “kA nAxt mry imn” (strong ox beloved of Amun) is one of Ramesses II five names.
I am glad that you and he had some fun with it!
Log in to reply
@Mark Hennings – You're right, about the Brilliant avatar thing making it look like an cartouche. I must admit that had been my first impression of it, and it was my fault for having gotten David (the Egyptologist) off on the wrong foot. It's such a popular thing to do, people looking up online "create your own cartouche!" to get totally anachronistic simulacrums. However, after I had studied yours, I realized that there was something more to it, but still missed the fact it isn't really a cartouche.
I'll pass your word to David, and thank you. He thanks you as well.
@Mark Hennings – David wants to share this with you:
Tiny details matter!
How did you deduce first identity?
Log in to reply
I am summing a geometric progression...
Log in to reply
I understood that, but I'm wondering how did you come up with it?
https://photos.app.goo.gl/s44ckcDS8bW5b8Qf6
If someone (mod) can convert it to a solution that would be a lot helpful.
Two thirds of the way down, the series ∑ k = 1 ∞ 2 k + 1 k ( − 1 ) k is an alternating series, the absolute values of whose terms are converging to 1/2, not 0, so shouldn't it diverge?
Log in to reply
Yeah, while solving it I thought of it, but my mind was confident to take the risk.
Have a look at my solution - you are attempting to manipulate divergent series, which is a dodgy thing to do...
Log in to reply
Yeah, while solving it I thought of it, but my mind was confident to take the risk.
It maybe dodgy as Mark says, but it's intriguing nevertheless. If we say that the divergent series
k ∑ ∞ ( − 1 ) k
"has an average of − 2 1 ", it works out neatly, i.e.,
2 ( − 2 1 + k = 1 ∑ ∞ 2 k + 1 ( − 1 ) k + 1 ) = 1 − 2 π
so it's fun to have a look at this "improper" approach
I’d highly suggest checking out Desmos or Wolfram Alpha.
I used Desmos.
Adding up consecutive terms, we see that the ( 2 n ) th gap is ∑ k = n ∞ ( 4 k + 1 4 − 4 k + 3 4 ) = ∑ k = n ∞ ( 4 k + 1 ) ( 4 k + 3 ) 8 . Likewise, the ( 2 n − 1 ) th gap is − ∑ k = n ∞ ( 4 k + 1 ) ( 4 k − 1 ) 8 . The sum of these two gaps is − ∑ k = n ∞ ( 4 k − 1 ) ( 4 k + 1 ) ( 4 k + 3 ) 3 2 , and the grand total of all gaps is − ∑ k = n ∞ ( 4 k − 1 ) ( 4 k + 1 ) ( 4 k + 3 ) 3 2 k = 2 1 ( 2 − π ) ≈ − 0 . 5 7 1 .
\sum _{n=1}^{\infty } \left(\pi -4 \sum _{k=1}^n \frac{(-1)^{k+1}}{2 k-1}\right)
is \sum _{n=1}^{\infty } 2 (-1)^n \Phi \left(-1,1,n+\frac{1}{2}\right)
Using Wolfram Mathematica 11.3.
Evaluating that expression numerically to machine precision, the answer is -0.570796326795 which is the answer given by Mark Hennings
Used Double Sum in WolframAlpha
(1) -0.5658 with 100 terms
(2) -0.5683 with 200 terms
(3) -0.5688 with 250 terms
(4) -0.5698 with 500 terms
(5) -0.57017 with 800 terms
Answer = -0.570
Far to be as elegant as Mark Hennings solution,
Just compute the formulas using a programming language
1 2 3 4 5 6 |
|
output: -0.5707967703631267
Hence the answer is aproximatively − 0 . 5 7 0 8
Since k = 1 ∑ n ( − 1 ) k + 1 x 2 ( k − 1 ) = 1 + x 2 1 − ( − x 2 ) n 0 < x < 1 we deduce that k = 1 ∑ n 2 k − 1 ( − 1 ) k + 1 = ∫ 0 1 1 + x 2 1 − ( − x 2 ) n d x = 4 1 π − ( − 1 ) n ∫ 0 1 1 + x 2 x 2 n d x so that π − 4 k = 1 ∑ n 2 k − 1 ( − 1 ) k + 1 = 4 ( − 1 ) n ∫ 0 1 1 + x 2 x 2 n d x for all integers n ≥ 1 . Thus S N = n = 1 ∑ N ( π − 4 k = 1 ∑ n 2 k − 1 ( − 1 ) k + 1 ) = 4 n = 1 ∑ N ( − 1 ) n ∫ 0 1 1 + x 2 x 2 n d x = − 4 ∫ 0 1 ( 1 + x 2 ) 2 x 2 ( 1 − ( − x 2 ) N ) d x from which it is clear that the infinite sum is S = − 4 ∫ 0 1 ( 1 + x 2 ) 2 x 2 d x The substitution x = tan θ gives S = − 4 ∫ 0 4 1 π sin 2 θ d θ = − 2 ∫ 0 4 1 π ( 1 − cos 2 θ ) d θ = 1 − 2 1 π