Sum of Sine Squares

$\begin{aligned} X & = \sin^2{18^\circ} + \sin^2 {30^\circ} \\ & = \frac {1}{2} (1 - \cos{36^\circ} )+ \frac{1}{4} \\ & = \frac{3}{4} -\frac{1}{2} \cos{36^\circ} \\ & = \frac{1}{2} + \frac{1}{2}\dot{}\color{#3D99F6}{\frac{1}{2}} - \frac{1}{2} \cos{36^\circ} \\ & = \frac{1}{2} + \frac{1}{2} \left(\color{#3D99F6}{\cos{36^\circ} + \cos{108^\circ}} - \cos{36 ^ \circ}\right) \quad \color{#3D99F6}{\text{[See Note]}} \\ & = \frac{1}{2} + \frac{1}{2} \cos{108^\circ} \\ & = \frac{1}{2} + \frac{1}{2}(2\cos^2{54^\circ}-1) \\ & = \cos^2{54^\circ} \\ & = \boxed{\sin^2{36^\circ}} \end{aligned}$

---

$\color{#3D99F6}{\text{Note:}}$

$\begin{aligned} \cos 36^\circ + \cos 108^\circ & = \cos 36^\circ + \cos (3(36^\circ)) \\ & = \cos 36^\circ + 4\cos^3 36^\circ - 3 \cos 36^\circ \\ & = 2 \cos 36^\circ (2\cos^2 36^\circ - 1) \\ & = 2 \cos 36^\circ \cos 72^\circ \\ & = 2 \cos 36^\circ \sin 18^\circ \\ & = \frac{2 \cos 36^\circ \sin 18^\circ \cos 18^\circ}{\cos 18^\circ} \\ & = \frac{\cos 36^\circ \sin 36^\circ}{\cos 18^\circ} \\ & = \frac{\sin 72^\circ}{2 \cos 18^\circ} \\ & = \frac{\cos 18^\circ}{2 \cos 18^\circ} \\ & = \boxed{\frac{1}{2}} \end{aligned}$

So instead of using identities, I resorted to using actual values and miraculously arrived to a solution. The reason I selected this approach was because 30º is a special angle and its sine can be easily computed; it's one half (simply draw an equilateral triangle, bisect one of the angles, and use the pythagorean theorem to determine the ratio of the sides). Therefore, I was able to collapse the problem a little bit.

$\sin^{2} (18) + \sin^{2} (30) = \sin^{2} (\theta)$ $\sin^{2} (18) + (\frac{1}{2})^{2} = \sin^{2} (\theta)$ $\sin^{2} (18) + \frac{1}{4} = \sin^{2} (\theta)$

Now, the sine of 18º is not as easily computable as that of 30º, but it can still be done. Take the following 72, 72, 36 triangle:

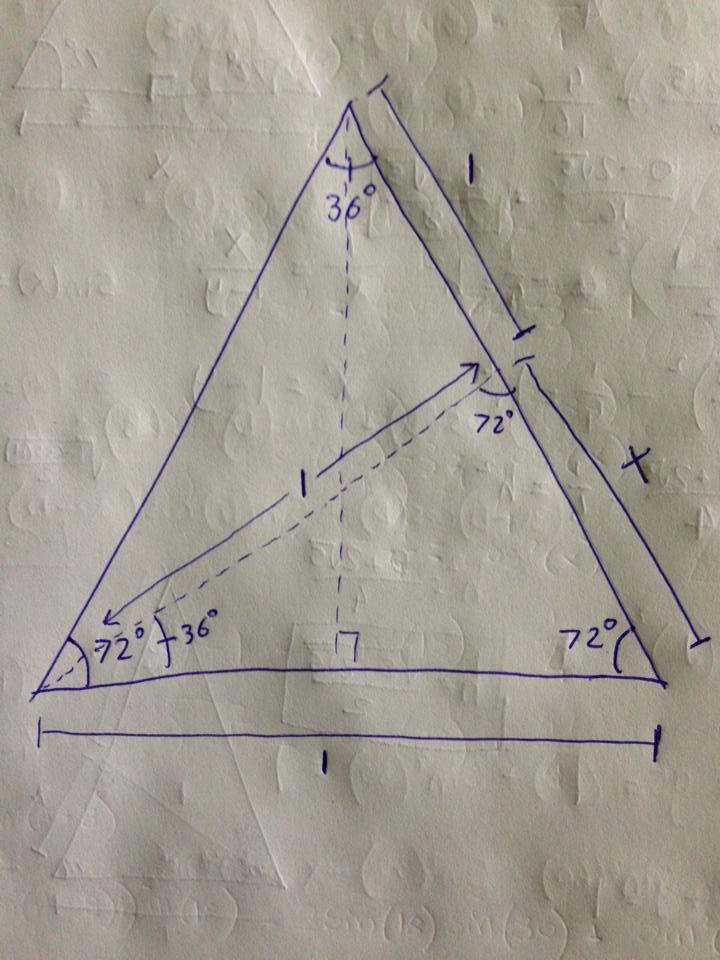
The non-vertical dotted line bisects the 72º angle on the left, thus creating a smaller 72, 72, 36 triangle at the bottom of the big triangle. I arbitrarily gave a length of 1 to the line that both triangles share. That line is opposite to one of the 72º of the small triangle; therefore, the line that is opposite to the other 72º angle of the small triangle should also have a length of 1; that happens to be the non-vertical dotted line. There is a third triangle: a 36, 36, 108 triangle that rests on top of the smaller 72, 72, 36 triangle. The non-vertical dotted line is opposite to one of the 36º angles of this new triangle; therefore, the line that is opposite to the other 36º angle of the new triangle should have the same length as the non-vertical dotted line, which happens to be 1. As a result the distance from the top of the big triangle to the point where the rightmost line of the big triangle and the non-vertical dotted line intersect is 1. The remaining portion of the rightmost line of the big triangle I simply labeled "X".

The two triangles that have 72º, 72º and 36º as their angles are similar. Therefore, we can write a simple ratio relating the lengths of the sides.

$\frac{opposite 72 big}{opposite 36 big} = \frac{opposite 72 small}{opposite 36 small}$ $\frac{1+X}{1} = \frac{1}{X}$

Cross multiply and simplify:

$(1+X)(X) = (1)(1)$ $X + X^{2} = 1$ $X^{2} + X - 1 = 0$

To solve for "X", use the quadratic formula. Keep in mind that "X" is a distance; therefore, only the positive value matters.

$X = \frac{-1 + \sqrt{1^{2} - 4(1)(-1)}}{2(1)}$ $X = \frac{-1 + \sqrt{1 + 4}}{2}$ $X = \frac{-1 + \sqrt{5}}{2}$

Now, to calculate the sine of 18, bisect the 36º angle of the big triangle. Because the big triangle is isosceles, the line that bisects the 36º angle also bisects the line with length 1 at the bottom. This new 18, 72, 90 triangle thus has a side of length 0.5 that is opposite the 18º angle and a hypotenuse of "1 + X". Because we now know the value of "X", we can compute the sine of 18.

$\sin \theta = \frac{opposite}{hypotenuse}$ $\sin (18) = \frac{ \frac{1}{2} }{1+X}$ $\sin (18) = \frac{ \frac{1}{2} }{1+ \frac{-1 + \sqrt{5}}{2} }$ $\sin (18) = \frac{ \frac{1}{2} }{ \frac{2}{2}+ \frac{-1 + \sqrt{5}}{2} }$ $\sin (18) = \frac{ \frac{1}{2} }{ \frac{2 -1 + \sqrt{5}}{2} }$ $\sin (18) = \frac{ \frac{1}{2} }{ \frac{1 + \sqrt{5}}{2} }$ $\sin (18) = \frac{1}{1 + \sqrt{5}}$ $\sin (18) = {\frac{1}{1 + \sqrt{5}}} \times {\frac{1 - \sqrt{5}}{1 - \sqrt{5}}}$ $\sin (18) = \frac{1 - \sqrt{5}}{ 1 - 5}$ $\sin (18) = \frac{1 - \sqrt{5}}{ -4 }$ $\boxed{ \sin (18) = \frac{\sqrt{5}-1}{ 4}}$

Now, back to the problem.

$\sin^{2} (18) + \frac{1}{4} = \sin^{2} (\theta)$ $(\frac{\sqrt{5}-1}{ 4})^{2} + \frac{1}{4} = \sin^{2} (\theta)$ $\frac{(\sqrt{5}-1)^{2}}{ 16} + \frac{1}{4} = \sin^{2} (\theta)$ $\frac{5 - 2\sqrt{5} + 1}{ 16} + \frac{4}{16} = \sin^{2} (\theta)$ $\frac{6 - 2\sqrt{5}}{ 16} + \frac{4}{16} = \sin^{2} (\theta)$ $\frac{10 - 2\sqrt{5}}{ 16} = \sin^{2} (\theta)$ $\frac{5 - \sqrt{5}}{8} = \sin^{2} (\theta)$ $\sin (\theta) = \frac{\sqrt{5 - \sqrt{5}}}{\sqrt{8}}$

We will now introduce the variable "U"

$U = 2\theta$ $\theta = \frac{U}{2}$ $\sin (\frac{U}{2}) = \frac{\sqrt{5 - \sqrt{5}}}{\sqrt{8}}$

Now, use the half angle identity. I am only concerned with the positive value because all of the angles are in the first quadrant.

$\sqrt{\frac{1 - \cos (U)}{2}} = \frac{\sqrt{5 - \sqrt{5}}}{\sqrt{8}}$ $\frac{1 - \cos (U)}{2} = \frac{5 - \sqrt{5}}{8}$ $8(1 - \cos (U)) = 2(5 - \sqrt{5})$ $4(1 - \cos (U)) = 5 - \sqrt{5}$ $4 - 4\cos (U) = 5 - \sqrt{5}$ $- 4\cos (U) = 1 - \sqrt{5}$ $\cos (U) = \frac{1 - \sqrt{5}}{-4} = \frac{\sqrt{5} - 1}{4}$

That number looks awfully familiar. As a matter of fact, we earlier determined that this number is the value for the sine of 18º (see the boxed value above).

$\cos (U) = \sin (18)$ $\sin (90 - U) = \sin(18)$ $90 - U = 18$ $U = 90 - 18$ $U = 72$ $2\theta = 72$ $\boxed{\theta = 36}$

We will prove that $\sin^2 18 ^ \circ + \sin ^2 30 ^ \circ = \sin^2 36 ^ \circ$ .

Here is a "pure synthetic geometry" proof of this result. Consider an icosahedron inscribed in a sphere of radius 1. Let the top vertex by $T$ and the bottom vertex by $B$ .

The bases of the 5 triangles that meet at $T$ would form a regular pentagon. Let these vertices be $T_1, T_2, T_3, T_4, T_5$ , and let this plane be $\Pi _T$ .

The bases of the 5 triangles that meet at $B$ would form a regular pentagon. These 2 pentagons are rotated from each other. Let these vertices be $B_1, B_2, B_3, B_4, B_5$ , where $B_1$ is between $T_1$ and $T_5$ . Let this plane be $\Pi _S$ .

Consider the projection of $T_1$ down onto $\Pi _ S$ and call it $P$ . Then, by definition $T_1 P B_ 1$ forms a right triangle at $P$ . We already have $T_1 B_1 = 2 \sin 36 ^\circ$ and $P B_1 = 2 \sin 18 ^\circ$ from the above discussion. Thus, we just have to show that $T_1 C = 2 \sin 30 ^\circ = 1$ .

This is pretty obvious and is left as an exercise to the reader.

Hint: Let $O$ be the center of the sphere. How do the points $T, O, S$ relate to planes $\Pi_T, \Pi_S$ ?

First we will prove that $\cos 72^\circ= \frac{\sqrt{5}-1}{4}$ . To do this we are going to use the fact that the complex fifth roots of 1, which are different from 1, are $w_{1}, w_{2}, \bar{w}_{1},$ and $\bar{w}_{2},$ where $w_{1}= \cos 72^\circ+i\sin 72^\circ$ and $w_{2}= \cos 144^\circ+i \sin 144^\circ.$ Then $(x-w_{1})(x-\bar{w}_{1})(x-w_{2})(x-\bar{w}_{1})=$ $= \frac{x^{5}-1}{x-1}= x^{4}+x^{3}+x^{2}+x+1.\:\:\:\:(*)$ Since $w_{1}+\bar{w}_{1} = 2\cos72^\circ$ , $w_{2}+\bar{w}_{2} = 2\cos 144^\circ$ , $w_{1}\bar{w}_{1} = 1$ , and $w_{2}\bar{w}_{2} = 1$ then the equation (*) can be written like this $(x^{2}- 2\cos 72^\circ x+1)(x^{2}- 2\cos 144^\circ x+1)= x^{4}+x^{3}+x^{2}+x+1.$ Expanding the product in the left side of the equation and making corresponding coefficients equal, we obtain the following equations

$\cos 72^\circ + \cos 144^\circ =-\frac{1}{2}$ and $\cos 72^\circ \cos 144^\circ =-\frac{1}{4}.$

Therefore $\cos 72^\circ$ , and $\cos 144^\circ$ will be the positive and the negative solutions, respectively, of the equation $z^{2} + \frac{1}{2}z-\frac{1}{4}=0.$ Therefore $\cos 72^\circ =\frac{\sqrt{5}-1}{4}$ . Now what follows is a lot easier $\sin^{2} 18^\circ+\sin^{2} 30^\circ =\cos^{2} 72^\circ+\sin^{2} 30^\circ=(\frac{\sqrt 5-1}{4})^{2}+(\frac{1}{2})^{2}=$ $=\frac{5-\sqrt 5}{8}= \frac{1-\frac{\sqrt 5 -1}{4}}{2}=\frac{1-\cos 72^\circ}{2}=\sin^{2} 36^\circ$

and then the answer must be $\sin^{2} 36^\circ.$

$\begin{aligned}\sin^{2}{18^\circ}+\sin^{2}{30^\circ}&=\sin^{2}{18^\circ}+\frac{1}{4}\\\\&=\sin^{2}{18^\circ}+\frac{-\cos{18^\circ}}{-4\cos{18^\circ}}\\\\&=\sin^{2}{18^\circ}+\frac{\cos{90^\circ}-\cos{18^\circ}}{-4\cos{18^\circ}}\\\\&=\sin^{2}{18^\circ}+\frac{-2\sin{54^\circ}\sin{36^\circ}}{-4\cos{18^\circ}}\\\\&=\sin^{2}{18^\circ}+\frac{-4\sin{54^\circ}\sin{18^\circ}\cos{18^\circ}}{-4\cos{18^\circ}}\\\\&=\sin{18^\circ}\left(\sin{18^\circ}+\sin{54^\circ}\right)\\\\&=2\sin{18^\circ}\sin{36^\circ}\cos{18^\circ}\\\\&=\color{#20A900}{\sin^{2}{36^\circ}}_\square\end{aligned}$

Let $\theta = 18^\circ$ $\Leftrightarrow 5\theta=90^\circ \Leftrightarrow \theta=90^\circ -4\theta \Leftrightarrow \cos\theta=\sin4\theta=4\sin\theta\cos\theta\cos2\theta$ $\Leftrightarrow 4\sin\theta\cos2\theta=1; [\because \cos\theta \ne 1]$ $\Leftrightarrow 4\sin\theta\cos(5\theta-3\theta)=1 \Leftrightarrow 4\sin\theta\cos(90^\circ-3\theta)=1$

$\therefore 4\sin\theta\sin3\theta=1$ ..........(i)

Now let

$\sin^2\alpha=\sin^{2}18^\circ+\sin^{2}30^\circ \Leftrightarrow \sin^2\alpha=\sin^{2}\theta+\frac{1}{4}$

$\Leftrightarrow 2\sin^2\alpha=2\sin^{2}\theta+\frac{1}{2}$

$\Leftrightarrow 1-\cos2\alpha=1-\cos2\theta+\frac{1}{2} \Leftrightarrow \cos2\theta-\cos2\alpha=\frac{1}{2}$

$\Leftrightarrow 2\sin(\frac{2\alpha+2\theta}{2})\sin(\frac{2\alpha-2\theta}{2})=\frac{1}{2}$

$\Leftrightarrow 4\sin(\alpha+\theta)\sin(\alpha-\theta)=1$ ..........(ii)

no(i) $\equiv$ no(ii) iff

$\alpha+\theta=3\theta$ and $\alpha-\theta=\theta$ $\iff \alpha=2\theta$ $\therefore \alpha=2\times 18^\circ=\boxed {36^\circ}$