Summer fun #20

I used a calculator

Adding $123456789$ to both sides gives:

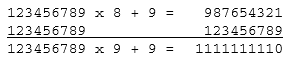
Adding another $123456789$ to both sides gives:

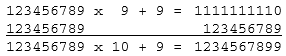
which is a true statement.

In general, if $A_k$ is a string of consecutive increasing digits from $1$ to $k$ , $B_k$ is a string of consecutive decreasing digits from $9$ to $10 - k$ , and $C_k$ is a string of $k$ $1$ 's followed by a $0$ , then by digit addition $A_k + B_k = C_k$ for $0 \leq k \leq 9$ and $10A_k + k = C_k + A_k$ for $0 \leq k \leq 9$ . Substituting gives $10A_k + k = (A_k + B_k) + A_k$ and simplifying gives $8A_k + k = B_k$ , which is the pattern given in the problem.

$\begin{aligned} N & = \dfrac{1}{9}\left(80\,(N_{k} -N_{k-1} )+k\right) \\& = \dfrac{1}{9}\left(80\,(1234\cdots 9 -1234\cdots 8) +9 \right)\\& = 987654321\end{aligned}$ where $N_{k}$ and $N_{k-1}$ are the numbers in which last digits ends at $k$ and $k-1$ . For example if $N_{k} = 1234$ then $N_{k-1}= 123$ .

Generalization

Notice that the number $1234\cdots k$ for $0 \leq k \leq 9$ be denoted as $N_k$ and further it can be expressed as $\begin{aligned} N & = 8\,(12345 \cdots\cdots k )+k = 8N_k +k \\& =8\,(\underbrace{111\cdots 1}_{\text{k 1's}}+ \underbrace{111\cdots 1 }_{\text{k-1 1's}} + \cdots 11 +1) +k \\& = \dfrac{8}{9}\left(\underbrace{999\cdots 9}_{\text{k 9's}}+ \underbrace{999\cdots 9 }_{\text{k-1 9's}} + \cdots 99 + 9 \right) +k \\& = \dfrac{8}{9}\left(10^k -1 +10^{k-1} -1 +\cdots 10^{1}-1\right) + k \\& = \dfrac{8}{9}\left(\dfrac{10\,(10^k-1)}{9}-k \right)+ k \end{aligned}$ Simplifying we obtain that $\begin{aligned} N & =\dfrac{8\cdot 10^{k+1}-80 -72k+81k }{81}\\& =\dfrac{80\cdot \,(10^{k}-1) +k\,(10-1) }{81}\\& = \dfrac{9}{81} \left(80\sum_{k=1}^{k-1} 10^k +k\right) \\ & = \dfrac{1}{9}\left(80\,(N_{k+1}-N_{k})+k \right) \end{aligned}$

Note: This pattern will continue till $k\leq 9$ but a new pattern will exist where formula works too. $\begin{aligned} 1234567890×8+0 & =9876543120 \\ 12345678901×8+1 & = 98765431209\\ 123456789012\times 8 +2 & =987654312098 \\\vdots \end{aligned}$

Generalization

In number base $b$ , it is generally true that for $1 \leq n \leq b-1$ , $\overline{123\cdots (n-1)\ n} \times (b-2) + n = \overline{(b-1)\ (b-2)\ \cdots (b-n+1)\ (b-n)}.$

Proof : $\begin{aligned} \overline{123\cdots (n-1)\ n} \times (b-2) + n & = \left(\sum_{i=1}^n i\cdot b^{n-i}\right)\cdot (b-2) + n \\ & = \left(\sum_{i=1}^n ib\cdot b^{n-i}\right) - \left(\sum_{i=1}^n i\cdot b^{n-i}\right) - \left(\sum_{i=1}^n i\cdot b^{n-i}\right) + n \\ & = \underbrace{\left(\sum_{i'=0}^{n-1} (i'+1)\cdot b^{n-i'}\right) - \left(\sum_{i=0}^{n-1} i\cdot b^{n-i}\right)}_{\text{combine}} - n\cdot b^{n-n} - \left(\sum_{i=1}^n i\cdot b^{n-i}\right) + n \\ & = \left(\sum_{i=0}^{n-1} (i+1-i)\cdot b^{n-i}\right) - \left(\sum_{i=1}^n i\cdot b^{n-i}\right) + \underbrace{ n - n }\\ & = \left(\sum_{i=0}^{n-1} b^{n-i}\right) - \left(\sum_{i=1}^n i\cdot b^{n-i}\right) \\ & = \underbrace{\left(\sum_{i'=1}^n b\cdot b^{n-i'}\right) - \left(\sum_{i=1}^n i\cdot b^{n-i}\right)}_{\text{combine}} \\ & = \sum_{i=1}^n (b-i)\cdot b^{n-i} \\ & = \overline{(b-1)\ (b-2)\ \cdots (b-n+1)\ (b-n)}. \end{aligned}$

I used a calculator for the solution.

From the three examples we observe this: 10^y(x) + 10^y-1(x+1).......10^0(x+y) × 8 + (x+y) = 10^y(n) +10^y-1(n-1)........10^0(n-y) for x=1,0< y < 9,and n=9. So for 123456789 we observe that y is 8. Next we substitute accordingly: 10^8(1) +10^7(2) +10^6(3) + 10^5(4) +10^4(5) + 10^3(6) +10^2(7) + 10^1(8) + 10^0(9) × 8 + (9) = 10^8(9) + 10^7(8) +10^6(7) +10^5(6) + 10^4(5) + 10^3(4) + 10^2(3) + 10^1(2) +10^0(1); So we get 100000000 + 20000000+3000000+400000+50000+6000+700+80+9 × 8 + 9 = 900000000+80000000+7000000+600000+50000+4000+300+20+1;This gives:123456789 × 8 + 9 = 987654321

Just use a calculator

I just answer yes

We start by expressing the left hand side $(L)$ and the right hand side $(R)$ in analytical form.

For a given integer $N$ with $N=[1,2,3,\cdots,9]$ we have $\begin{aligned} L(N)=8* \sum_{n=1}^N n*10^{N-n}+N \end{aligned}$ $\begin{aligned} R(N)=\sum_{n=1}^N(10-n)*10^{N-n} \end{aligned}$ For example, for $N=1$ $\begin{aligned} L(1) = 8*(1*10^{1-1}) + 1 = 9\end{aligned}$ $\begin{aligned} R(1) = (10-1)*10^{1-1} = 9 \end{aligned}$

and for $N=3$ $\begin{aligned} L(3)=8*(1*10^{3-1}+2*10^{3-2}+3*10^{3-3})+3=8*123+3=987\end{aligned}$ $\begin{aligned} R(3)=9*10^{3-1}+8*10^{3-2}+7*10^{3-3}=900+80+7=987\end{aligned}$ .

To prove that $L(N)=R(N)$ for all integers $N$ , $1 \leq N \leq 9$ one could show that the expression for $L(N)$ can be reduced to the one for $R(N)$ (or vice-versa) for $N$ in the range of interest.

An alternate approach is to use recursion i.e. express $L(N+1)$ as a function of $L(N)$ and similarly for $R(N+1)$ . From the analytical forms above for $L(N)$ and $R(N)$ one finds that $\begin{aligned} L(N+1) = 10*L(N) - N + 9 \end{aligned}$ $\begin{aligned} R(N+1) = 10*R(N) - N + 9 \end{aligned}$

Since $L(1)=R(1)$ , it follows that $L(N) = R(N)$ for $1 \leq N \leq 9$ .

I just added last digit of 8x9 with 9 to see if last digit comes out as 1

The method that I used was that in the first sum they gave us 1 that's the first number in the order of first to last the answer to that sum was 9 and that was the first number in the order of last to first and if u see the last sum the first number they give is the number 1-9 in the order of first to last and the answer to that sum was 1-9 but in the opposite order to the first number so the sum must have been correct

there's a pattern of complimentary. For e.g. complimentary of 1 is 9, while their sum must be 10, i.e 1+9=10, subsequently 2+8=10, 3+7=10, 4+6=10. Starting from right. For 12, complimentary for individual 1 and 2 are 9 and 8. For 123 complimentary for 1,2 and 3 are 9,8 and 7 respectively. On applying this to 123456789, complimentary for individual digits become 987654321. I solved it like that.

1 x8+1=9 ;- 1+9=10 12 ×8+1=98 ;- 1+9=2+8=10 that's the pattern i think

I used pencil and paper and regular multiplication and addition

The number added is the same as the amount of digits in the first and last number given in each equation. The one in question follows

No “muh calculator” needed...

It's like when you see in example No.1, 1×8+1=9 we see two last numbers 1 and 9 with equals 10. At the example No.2 we see the same thing 12×8+2=98 with we see 2 added this time and last digit is 8 which equals 10. The last example is the same 123×8+3=987 3(added) and last digit we see 7 are both giving us 10.

Which moving to actual statement 9+1=10 so this has to be true.

Ps. Sorry if something doesn't make sense, English is not my first language.

Use a calculator.

Abductive Logic; C.S. Peirce; from Harvard circa ~1840ish; a.k.a. discovery logic/educated guess. Frrom final digit number in statement; worked via the provided pattern construct; yielding a final digit, matching that in the statement provided - I took a leap of faith; guessed re the match; ended up being right !!

The number added =to th e number of digits of answer

9=1

My trusty calculator is the reason we humans do not tear our brains apart

I took a healthy guess

It is simple.

The first three problems go by the next formula.

(x) x 8 + (n) = (r).

• x going by the digits on increasing ratio starting by 1 (like 1,12,123 and etcetera).

• n going by the number of digits of x number.

• r going by the result that is easily digits on decreasing ratio starting by 9 but just allowing the number of digits that n tolds us.

So just by checking this formula on the forth problem we can tell that is true.

ps. Sorry don't know how to use latex but this is the only way i can explain how i resolve this problem also english isnt my native lang so it may be kinda sketchy to read.

It can be proved by mathematical induction (at a mini scale):

First one is obviously true: $1 \times 8 + 1 = 9$

The problem is to prove： $S_{n} = 12...n \times 8 + n = 9...(10-n)$

given that: $S_{n-1} = 12...(n-1) \times 8 + n-1 = 9...(9-n)$

Actually we just needed to do some algebra with: $S_{n} = S_{n-1} \times 10 + 9-n$ .

Then it will become Sn on both sides and end of proof!

I Used My Mind

Logic. There was a pattern for the first 3, so why would it change. The pattern remained for the question so logically the question was correct.

Ideally, first of all you should multiply 123456789 with 8. So I just multiplied their last digits i.e 9×8=72. So you know the answer's last digit is 2. Then 2+9 is 11. The last digit of your final answer should be 1 which corresponds to 987654321

My idea was to multiply the long number by ten then substract the double of the first digit which is 9 so the double is 18 then 0-8 practically will give 2. Adding 9 to it will give 1 at the first digit of the result. Thus the answer was correct. This was my method

Hello,

Here is how I get it:

Suppose that $n \leq 9$ and the $n^{th}$ equation can be written as $k_n = \left(\sum_{i=1}^n 10^{n-i}.i\right) .8 + n = (1234...n) . 8 + n$ Then $\begin{array}{rcl} k_{n+1} &=& \left(\sum_{i=1}^{n+1} 10^{n+1-i}.i\right) .8 + n+1 \\ & = & 10. \left(\sum_{i=1}^n 10^{n-i}.i\right) .8 + 8(n+1) + n+1 \qquad \textrm{i.e. removing i=n+1 from the sum} \\ & = & 10. \left(\sum_{i=1}^n 10^{n-i}.i\right) .8 + 10.n - 10.n + 8(n+1) + n+1 \qquad \textrm{i.e. adding \& removing 10n} \\ & = & 10. \left[ \left(\sum_{i=1}^n 10^{n-i}.i\right) .8 +n \right] + 9 - n \\ & = & 10.k_n + 9 - n \end{array}$ or switching $n+1$ by $n$ $k_n = 10 k_{n-1} + \left( 10 - n\right)$

Since it holds for $n=1$ , one can show that it holds for $n=2$ and so on.

Knowing that it then holds for $n=8 \Rightarrow k_8 = 98765432$ , one can get that $k_9 = 10.k_8 + (10-9) = 987654321$

Simply check the first and last digits to approximate the solution.

9 x 8 = 72 + 9 = _1

8 x 1 = 8 + 1 (carried over) = 9

The first, and more importantly, last digits work out, so it is likely correct.

Note: this is not a guaranteed method, it is just a quick approximation.

Just a note of interest:

1
2
3
4
5
6

123456789×8+9 = 987654321
1234567891×8+91 = 9876543219
12345678912×8+902 = 98765432198
123456789123×8+9003 = 987654321987
1234567891234×8+90004 = 9876543219876
...

Easy problem! Just use a calculator haha.

I did 123 x 8 + 1 and got it. So I did 123456789 x 8 + 9 and it had to be true.

1+1👌👌 uso talaga to isigaw mo gago!!! 😏😏😏😏

$321 - 9 = 312$

Now, since $312$ is divisible by $8$ and $987654000$ is also divisible by $8$ then this statement is definitely true.

Let $a_{n} = n$ for $n = \left\{1, 2, 3, \cdots , 8, 9\right\}$ . It follows that $a_{n} = a_{n-1} + 1.$ Then, we have: $\begin{aligned} S_{n} &= \overline{123\cdots a_{n-1}a_{n}}\times 8 + a_{n} \\ &= 10\times \overline{123\cdots a_{n-1}}\times 8 + 9a_{n} \\ &= 10\times \overline{123\cdots a_{n-1}}\times 8 + 9a_{n-1} + 9 \\ &= 10\times \left ( \overline{123\cdots a_{n-1}}\times 8 + a_{n-1}\right) + \left ( 9-a_{n-1} \right ) \\ &= 10\times S_{n-1} + 10 - a_{n} \\ S_{n} &= 10\times(S_{n-1}+1) - n \end{aligned}$ We can see that this indeed follows the given patern. So without explicitly calculating, based on first simple cases, we can conclude that the statement is true.