Summer of 69!
∫ ( x + x 2 + 1 ) 6 9 d x
If the indefinite integral above is of the form:
b a ⎣ ⎡ c ( x + x 2 + 1 ) c + d ( x + x 2 + 1 ) d ⎦ ⎤ + α
where α is constant of integration.
c > d
Find a + b + c − d .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Nice! That's an interesting approach. Thanks for the variety!
Good method +1.
Log in to reply
Thanks. Cheers!!
Log in to reply
U r in which class??
Log in to reply
@Aditya Kumar – Will start attending IIT - Hyderabad this year. Chemical Engineering.
Log in to reply
@Vishwak Srinivasan – Awsome! IIT after all is awsome! What was ur rank??
Log in to reply
@Aditya Kumar – Bad. 4637.
I = ∫ ( x + x 2 + 1 ) n d x l e t x + x 2 + 1 = t a n d ( 1 + x 2 + 1 x ) d x = d t ∴ I = 2 1 ∫ t n − 2 ( t 2 + 1 ) d t O n s o l v i n g , I = 2 1 [ n + 1 ( x + x 2 + 1 ) n + 1 + n − 1 ( x + x 2 + 1 ) n − 1 ] + α o n s u b s t i t u t i n g v a l u e s , a + b + c − d = 1 + 2 + 7 0 − 6 8 = 5
Moderator note:
Great work!
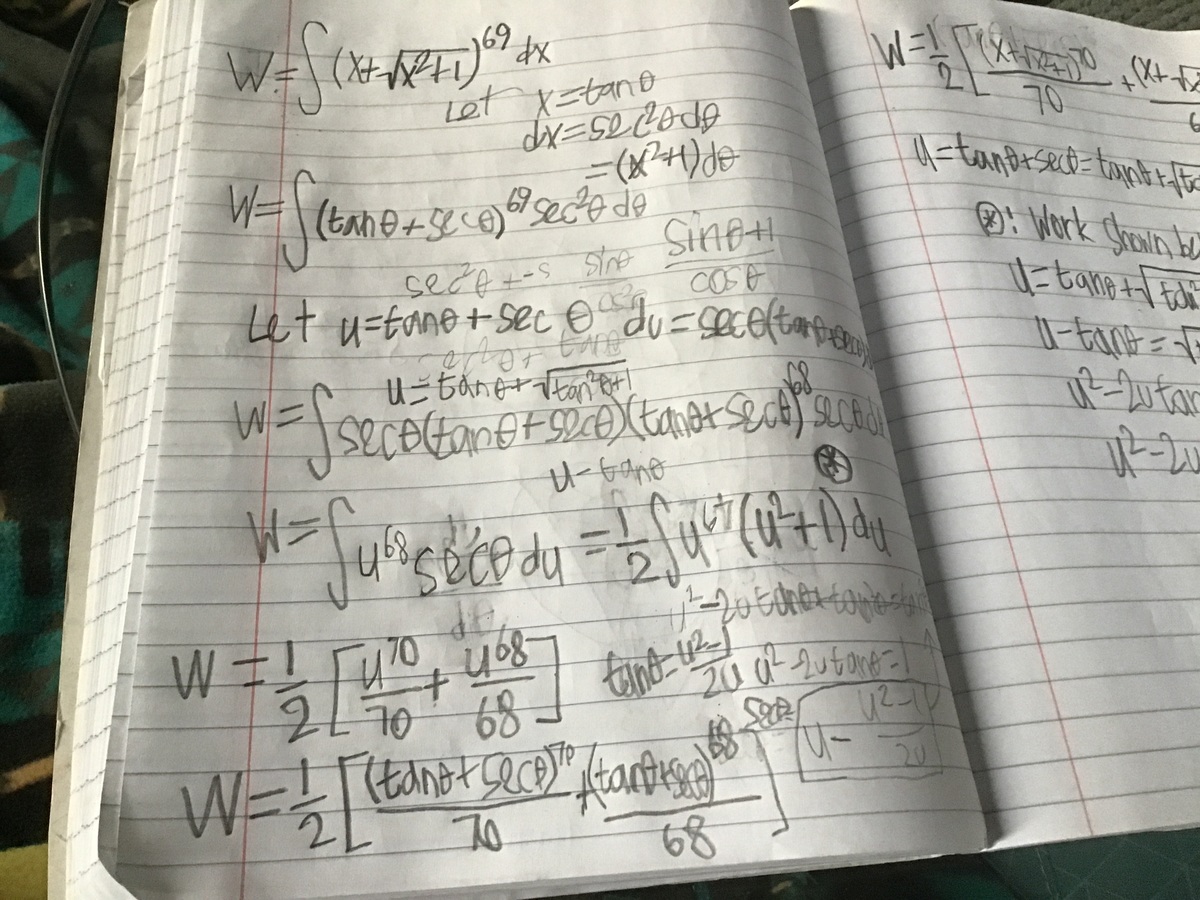

For the sake of variety, I tried this:
Let t = ln ( x + x 2 + 1 )
⇒ d t = x + x 2 + 1 1 ( 1 + x 2 + 1 x ) d x = x 2 + 1 1 d x
− t = − ln ( x + x 2 + 1 ) = ln ( x 2 + 1 − x )
⇒ e t = x + x 2 + 1
⇒ e − t = − x + x 2 + 1
⇒ x 2 + 1 = 2 1 ( e t + e − t ) ⇒ d t 2 1 ( e t + e − t ) = d x
I = 2 1 ∫ e 6 9 t ( e t + e − t ) d t = 2 1 ∫ e 7 0 t d t + 2 1 ∫ e 6 8 t d t
I = 2 1 ( 7 0 e 7 0 t + 6 8 e 6 8 t ) + α
I = 2 1 ( 7 0 ( x + x 2 + 1 ) 7 0 + 6 8 ( x + x 2 + 1 ) 6 8 ) + α
a = 1 , b = 2 , c = 7 0 , d = 6 8 ⇒ a + b + c − d = 5