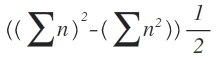Generalize This!
( x − 1 ) ( x − 2 ) ⋅ ⋅ ⋅ ( x − n )
The coefficients of x n − 2 in the expansion above is equals to?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Haha , I used the same method too . But being the clumsy person that I am , I clicked the wrong option .
( x − 1 ) . ( x − 2 ) . . . ( x − n ) = x n − ( 1 + 2 + ⋯ + n ) x n − 1 + ( Sum of product of two the two integers taken two at a time ) x n − 2 + …
Now what we are interested in is "Sum of product of two the two integers taken two at a time"
We know that for two numbers a , b , a b = 2 ( a + b ) 2 − ( a 2 + b 2 )
So we use analogy to apply it to n.
"Sum of product of two the two integers taken two at a time" = 2 ( ∑ n ) 2 − ∑ n 2
Always remember... (square of sums-sum of squares) by 2. Upvoted
I'd have posted this as a solution, but since I'm too late to the party, let me present my approach which is far more simpler and easier to grasp. We'll make use of Vieta's formulas and Newton's Identities.
As usual, we denote P i and e i as the i th power sum of the roots and elementary symmetric polynomial respectively for the given polynomial. For the given problem, we have,
e 1 = P 1 = ∑ n ; P 2 = ∑ n 2
From Vieta's formulas, we know that the required coefficient is simply e 2 .
We use the following identity from Newton's Identities:
P 2 = e 1 P 1 − 2 e 2 ⟹ e 2 = 2 1 ( ( P 1 ) 2 − P 2 ) ⟹ e 2 = 2 1 { ( ∑ n ) 2 − ∑ n 2 }
Log in to reply
Yah , you really are late ! It's 2:40 am :)
Log in to reply
Well, I slept through the day, so I came here now. #Insomniac
Log in to reply
@Prasun Biswas – I guess I am the same as you then ! I'll now wake up in the afternoon .
Log in to reply
@A Former Brilliant Member – Same here, dude! Who knows, maybe I'll sleep through the afternoon as well! I'm gonna get screwed in the physics exam though. I haven't read a thing till now. I wasted almost 3-4 days :(
Log in to reply
@Prasun Biswas – Ditto ! I was busy studying Vector fields and Line Integrals that I forgot to study communications and semiconductors !
Log in to reply
@A Former Brilliant Member – I almost spent most of my time on Brilliant. Damn, I'm addicted to it.
Log in to reply
@Prasun Biswas – Again same here !!! Btw I'll get back to study , else I ll end up flunking on Monday !!
Log in to reply
@A Former Brilliant Member – Yes, I need to log off too. I have to start practicing the derivations again. Man, I hate physics and chemistry! >_<
Great solution this is
As it is a MCQ problem, put n=2 and check the options..
The expression will be in the form
for getting coefficient of x^n you should take x from each of the brackets so coeff will be 1 similarly for x^n-2 you should take x from n-2 brackets and numbers from remaining 2 brackets so we will get the term 1.2+1.3+1.4+....+2.3+2.4.... multiplication of all the numbers taken two at a time whose summation is