Summing Up Certain Roots of Unity
Let ω = e 1 0 2 π i , which is a primitive 1 0 th root of unity.
Consider all solutions to + a 0 × 1 a 5 × ω 5 + a 1 × ω 1 + a 6 × ω 6 + a 2 × ω 2 + a 7 × ω 7 + a 3 × ω 3 + a 8 × ω 8 + a 4 × ω 4 + a 9 × ω 9 = 0 , where a i ∈ { 0 , 1 } . For each solution, define A = ∑ a i .
Over all possible solutions, how many distinct values of A are there?
As an explicit example, we could have all a i = 1 , which gives us A = 1 0 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since a i is either 0 or 1 , then we can imagine adding unit vectors from the center to the vertices of a decahedron. We want to know which combinations of vectors add up to 0 . It immediately becomes obvious that 0 and 1 0 vectors will add up to nothing, and that any opposite pairs of vectors will also add up to nothing, and that 5 vectors equally spaced, i.e., a pentagon, will add up to nothing. Meanwhile, obviously a single vector remains a single vector, which means its complement of 9 vectors will also add up to a single vector. We're then left with 3 vectors to look at (and its complement, 7 vectors)---and it's easy to see that for 3 vectors to add up to nothing, they have to be at angles of 1 2 0 degrees apart, which is impossible here (which means that its complement of 7 vectors is also impossible).
Hence we've got 0 , 2 , 4 , 5 , 6 , 8 , 1 0 vectors that can add to nothing, while 1 , 3 , 7 , 9 vectors cannot add to nothing.
When I first tackled this problem, I missed the detail that a i can only be either 0 or 1 . Much easier with this particular condition! But this gives me a great idea for a new problem.
Log in to reply
Yes, that's the simplified idea of the above proof. Can you post it as a separate solution?
I presented it this way as I wanted to generalize it to 2 p directly, and the proper argument for "you can't select a non-empty subset of those p vectors to get it to sum to 0" is essentially about the complex roots of unity.
In relation to your last comment, relaxing the constraint on a i leads to solutions which are essentially linear combinations of these types of equations that we found. For a concrete reason why, we would have to go deeper into Galois theory.
This is a simplified solution based on Calvin's fuller explanation, to help better understand it
Since a i is either 0 or 1 , then we can imagine adding unit vectors from the center to the vertices of a decahedron. We want to know which combinations of vectors add up to 0 . It immediately becomes obvious that 0 and 1 0 vectors will add up to nothing, and that any opposite pairs of vectors will also add up to nothing, and that 5 vectors equally spaced, i.e., a pentagon, will add up to nothing. Meanwhile, obviously a single vector remains a single vector, which means its complement of 9 vectors will also add up to a single vector. We're then left with 3 vectors to look at (and its complement, 7 vectors)---and it's easy to see that for 3 vectors to add up to nothing, they have to be at angles of 1 2 0 degrees apart, which is impossible here (which means that its complement of 7 vectors is also impossible).
Hence we've got 0 , 2 , 4 , 5 , 6 , 8 , 1 0 vectors that can add to nothing, while 1 , 3 , 7 , 9 vectors cannot add to nothing.
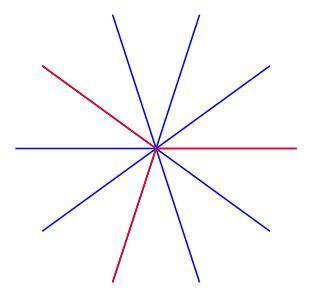
Here's a graphic showing 3 red (or 7 blue) vectors, neither combination adding up to a null vector
1) We can easily see that the equation is valid for, a i = 0 ⇒ ( A = 0 ) is valid
2) We know that,
ω 1 0 = 1 ⇒ ω 1 0 − 1 = 0
thus ω − 1 ω 1 0 − 1 = ∑ i = 0 9 ω i = 0 ⇒ ( A = 1 0 ) is valid
3) ω 5 = − 1 ⇒ ω 5 + 1 = 0 ⇒ ( A = 2 ) is valid
multiplying throughout by ω we get 4 more pairs
ω 6 + ω = 0
ω 7 + ω 2 = 0
ω 6 + ω 3 = 0
ω 6 + ω 4 = 0
4) Adding distinct pairs from the set of 5 pairs above would give another valid case, thus we can see that it is valid for ( A = 4 , 6 , 8 )
5) ( ω 5 ) 2 = 1 ⇒ ω 2 − 1 ( ω 2 ) 5 − 1 = 1 + ω 2 + ω 4 + ω 6 + ω 8 = 0 ⇒ ( A = 5 ) is valid
6) now we need to show it is impossible for A = 1 , 3 , 7 , 9
i) Case 1 : ( A = 1 )
we know that ω 1 0 = 1 so, ω n = 0
thus we have no solution for A = 1
ii) Case 2 : ( A = 3 )
assume it is valid for A = 3
then ω a + ω b + ω c = 0 where a,b,c are distinct and 0 ≤ a , b , c ≤ 9 assume a to be the smallest then we have
ω a ( 1 + ω b − a + ω c − a ) = 0 ⇒ ω b − a + ω c − a = − 1 , ( b − a ) and ( c − a ) are distinnct.
since the RHS is purely real and negative we need to check only 2 cases,namely,
ω 6 + ω 4 and ω 7 + ω 3
since both of these doesn't satisfy the equation there is no solution for A = 3
iii) Case 3 : ( A = 7 , 9 )
we can see that
ω 5 + x + ω x = 0
when we select 7 distinct powers of ω we will always have 2 pairs that add upto 0 ,
thus it reuces to the case where A = 3
similary when we select 9 distinct powers of ω we will always have 4 pairs that add upto 0 ,
thus it reuces to the case where A = 1
since we already proved that A = 1 , 3 ,we can see that A = 7 , 9
thus the possible distinct values of A are A = 0 , 2 , 4 , 5 , 6 , 8 , 1 0
the number of distinct values of A are 7
sorry for the tedious approach,i'm sure there are more elegant solutions,but this is what i could come up with
Great. How can we generalize this?
@Brandon Monsen approached me with the problem for n = 4 0 3 4 instead of 10. Listing through all of the cases would be quite painful.
Log in to reply
Curse the all 0 case! Anyways I still don't really have a grasp as to what's going on with these cyclotomic polynomials you mentioned in slack but after looking at wikipedia they gave some generalizations as to what these polynomials will look like for different n .
More importantly, the cyclotomic polynomial Φ n ( x ) , which is the minimal polynomial for x = e 2 π n 1 is given by
Φ n ( x ) = 1 ≤ k ≤ n , g c d ( k , n ) = 1 ∏ ( x − e 2 π n k )
Since our ω k represents some member of the set S where S = { e 2 π n k } k = 1 , 2 , 3 , . . . , n , these minimal polynomials represent the smallest possible "cycle" that sums to 0 for any given k .
Since we have the smallest cycle, we can form other cycles by multiplying the minimal polynomial by other polynomials M ( x ) such that Φ n ( x ) M ( x ) = ∑ p = 0 q a p x p = 0 for a p = 0 , 1 .
And yet still I have no idea how to show that those are the ONLY possibilities. Do all polynomials P ( x ) such that k is a root contain a factor that is the minimal polynomial of k ?
if ( ω p ) q = 1
then 1 + ω p + ω 2 p + . . . . + ω p ( q − 1 ) = 0
thus A=q will be valid
also we can multiply 1 + ω p + ω 2 p + . . . . + ω p ( q − 1 ) by ω p , p − 1 more times to get p distinct equations of length q
thus A = q , 2 q , 3 q , . . . . . . . . , p q will all be valid
by interchanging p and q in ( ω p ) q
we can get get q distinct equations of length p also
thus A = p , 2 p , 3 p , . . . . . . . . , p q will also be valid
thus the total number of cases of A for a given p and q comes out to be p + q − m
where m = l c m ( p , q ) p q
so we need to find all such pairs p and q,and also add the trivial case where A = 0
these are my thoughts
Log in to reply
I had come up with something similar to that earlier, where the factors of n were the "cycle"-lengths ie how many terms you add up, with the other factor being the increment on the exponents. I'm trying to show now that there are no other possibilities, ie x 2 + x 2 4 + x 1 3 5 + x 1 3 6 = 0 .
Calvin had pointed out minimal polynomials for a certain root k , which are the least degree polynomial with integral coefficients such that k is a root, and I'm trying to use that to prove how the cases you named are the only ones.
That's a good start.
-
I believe you're already using the fact that p , q are primes, or that l c m ( p , q ) = 1 . The case when l c m ( p , q ) = 1 is more complicated.
-
Your argument only shows sufficiency / existence. It doesn't show necessity (which is the later half of your solution arguing that A = 1 , 3 , 7 , 9 ).
Log in to reply
@Calvin Lin – Did you look at what I posted? I was curious if all polynomials with integral coefficients such that k is a root would be of the form f ( x ) M ( x ) where f ( x ) is an arbitrary polynomial and M ( x ) is the minimal polynomial of k ?
My intuition says yes, and I worked out the case for 2 in a cubic polynomial to get an idea of what's going on:
P ( x ) = ( x − 2 ) ( x − a ) ( x − b ) P ( x ) = x 3 − ( 2 + a + b ) x 2 + ( 2 a + 2 b + a b ) x − a b 2 a b = 2 p , p ∈ Z 2 ( a + b ) + a b = q , q ∈ z , a + b = r − 2 , r ∈ z ⇒ 2 ( r + 2 p ) = q + 2 ⇒ p = − 2 r , q = − 2 a b = − 2 r , 2 a + 2 b = 2 r − 2 ( a + 2 ) ( b + 2 ) = 0
Therefore either a or b must be − 2 for P ( x ) to have a root 2 and also have integral coefficients.
Obviously this doesn't prove it for all cases, but I was wondering if I should continue down this road?
Log in to reply
@Brandon Monsen – Yea i did. It wasn't clear to me where you were going with it though.
Log in to reply
@Calvin Lin – Oh I was thinking that given the constraint a i = 0 , 1 , we could write all polynomials such that k is a root in the form f ( x ) M ( x ) , where M is the minimal polynomial of k .
If this were true, then we would be able to look for the other possible solutions by adding\subtracting iterations of M ( x ) x α for some values of α such that all coefficients are 1 or 0 .
Essentially it would be transforming the problem such that we would be dealing with basic arithmetic of like terms rather than adding vectors in the complex plane, and the answers would be much easier to arrive to.
We can have A = 0 , 2 , 4 , 5 , 6 , 8 , 1 0 , for a total of 7 values.
The trickier part is explaining why these are the only solutions, and how we can generalize the approach. Read on for how to do this.
We will answer the general question for n = 2 p , where p is an odd prime. In this case, we have p = 5 .
Claim: The number of values of A is p + 2 . These correspond to the p + 1 even numbers 0 , 2 , … , 2 p and the odd number p .
Proof: First, we show why those numbers work.
In the even case, for A = 2 k , observe that since ω p = − 1 , thus ω i = − ω p + i . We can set a 1 = a 2 = … = a k = 1 , a p + 1 = a p + 2 = … = a p + k = 1 , and a i = 0 otherwise. Then, since ω i + ω p + i = 0 , thus the terms can be paired up and sum to zero.
In the odd case, for A = p , we set a 2 = a 4 = a 6 = … = a 2 p = 1 , and a i = 0 otherwise. Notice that ω 2 k correspond to the k roots of unity.
Now, we will show why these are the only numbers which work.
Let x = ω 2 . Then, x is a primitive p root of unity.
Now, rewrite the original equation as:
( a 0 − a p ) 1 + ( a 2 − a p + 2 ) x + ( a 4 − a p + 4 ) x 2 + … + ( a 2 p − 2 − a p + ( 2 p − 2 ) ) x p − 1 = 0 ,
where the indices are evaluated modulo 2 p , meaning that a 3 p − 2 = a p − 2 .
Then, by the previous claim, the only solutions occur when these values of a 2 k − a 2 k + p are all equal.
Since a i ∈ { 0 , 1 } , hence a 2 k − a 2 k + p ∈ { 0 , 1 , − 1 } .
In the event that a 2 k − a 2 k + p = 1 , we must have a 2 k = 1 , a 2 k + p = 0 , which gives A = p .
In the event that a 2 k − a 2 k + p = − 1 , we must have a 2 k = 0 , a 2 k + p = 1 , which gives A = p .
In the event that a 2 k − a 2 k + p = 0 , we must have a 2 k = a 2 k + p , which gives that A is even.
Hence, these are the only numbers which would work.
This solution can be generalized using group theory , specifically Galois theory. It does exactly what we need with the coefficients, and yields that the only values of A which work are when g cd ( n , A ) = 1 . In particular, for n = 1 5 , the only possible values of A are indeed 0 , 3 , 6 , 9 , 1 2 , 1 5 , 5 , 1 0 .
I do not yet know how of an elementary solution to deal with n = p q . The minimal polynomial trick no longer works, because with x = ω p , we have coefficients of the form a i + a i + q ω q + a i + 2 q ω 2 q + … , which need not be an integer (and in fact are often complex valued).