Super Node
What is the voltage at the node indicated by the red dot?
Details and Assumptions:
- All three DC voltage sources are ideal (zero internal impedance).
- The sources on the left and right have their negative terminals at reference potential.
The answer is 2.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I do not think you can make something to a super node, if there is a voltage source in it. I defined a current through that source, and I had three loop laws and two node laws. I solved for all five currents. I got V=3.75V.
Log in to reply
That's a good suggestion (solving using meshes as a double-check). When I do so, I get the same answer as with the super node method. I have appended that solution to the original solution.
Log in to reply
You are right (again). My number corresponds to your I3.
Log in to reply
@Laszlo Mihaly – Ok, thanks. It's interesting to note that we can reduce the level of abstraction (ditch the superposition) by defining more variables, as seemed to be your approach.
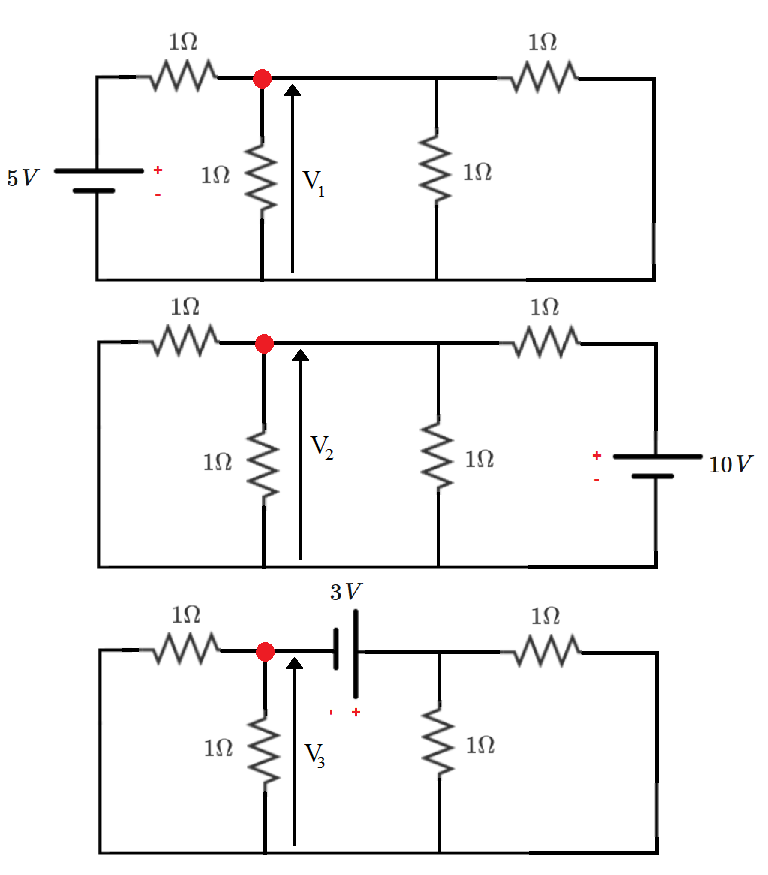 We can solve the problem using superposition theorem, by short-circuiting two voltage sources and considering only one voltage source at a time and then add the three voltages at the node at the end. Referring to the figure:
We can solve the problem using superposition theorem, by short-circuiting two voltage sources and considering only one voltage source at a time and then add the three voltages at the node at the end. Referring to the figure:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ V 1 = 1 + 1 ∣ ∣ 1 ∣ ∣ 1 1 ∣ ∣ 1 ∣ ∣ 1 × 5 = 1 + 3 1 3 1 × 5 = 4 5 V V 2 = 1 + 1 ∣ ∣ 1 ∣ ∣ 1 1 ∣ ∣ 1 ∣ ∣ 1 × 1 0 = 1 + 3 1 3 1 × 1 0 = 2 5 V V 2 = 1 ∣ ∣ 1 + 1 ∣ ∣ 1 1 ∣ ∣ 1 × ( − 3 ) = 2 1 + 2 1 2 1 × ( − 3 ) = − 2 3 V
Then, the voltage at the node V n o d e = V 1 + V 2 + V 3 = 4 5 + 2 5 − 2 3 = 4 9 = 2 . 2 5 V .
There is no impedance associated with the middle voltage source, so we can't define a current through that source the way we usually do with nodal analysis. Instead, treat the highlighted region as a "super node" and account for the fact that the sum of the currents flowing out of it must be zero.
( V − 5 ) + V + ( V + 3 ) + ( V + 3 − 1 0 ) = 0 4 V = 9 V = 2 . 2 5
It is also possible to solve this using current meshes, as shown below. It is important to note that some of the resistors (the "shunt" resistors) have currents which are superpositions of the defined loop currents.
KVL equations:
5 − I 1 − ( I 1 − I 2 ) = 0 − ( I 2 − I 1 ) + 3 − ( I 2 − I 3 ) = 0 − ( I 3 − I 2 ) − I 3 − 1 0 = 0
This yields the following:
I 1 = 2 . 7 5 I 2 = 0 . 5 I 3 = − 4 . 7 5
And the node voltage of interest is:
V = 5 − I 1 = 5 − 2 . 7 5 = 2 . 2 5 V = 1 0 + I 3 − 3 = 1 0 − 4 . 7 5 − 3 = 2 . 2 5