Super Rads

Calculus Level 3

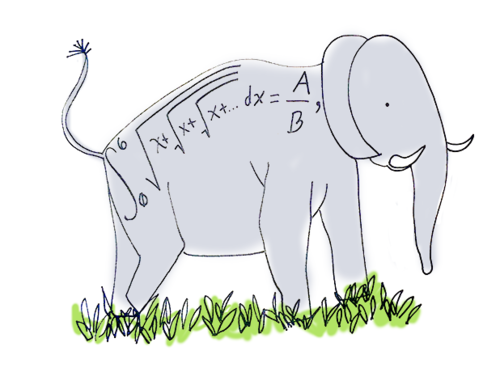$\int_0^6\sqrt{x+\sqrt{x+\sqrt{x+\ldots}}}\text{ }dx=\dfrac{A}{B},$

where $A$ and $B$ are positive coprime integers. Find $A+B$ .

The answer is 43.

3 solutions

Trevor B.
Apr 17, 2014

First simplify the radical expression.

Let $y=\sqrt{x+\sqrt{x+\sqrt{x+\ldots}}}.$ $\begin{aligned} y&=\sqrt{x+\sqrt{x+\sqrt{x+\ldots}}}\\ y&=\sqrt{x+y}\\ y^2&=x+y\\ y^2-y&=x\\ y^2-y-x&=0 \end{aligned}$ You can use the quadratic formula to solve for $y$ in terms of $x.$ $y=\dfrac{1+\sqrt{1+4x}}{2}$ Now resubstitute this into the integral. $\begin{aligned} \int_0^6\dfrac{1+\sqrt{4x+1}}{2}\text{ }dx&=\int_0^6\dfrac{1}{2}\text{ }dx+\int_0^6\dfrac{\sqrt{4x+1}}{2}\text{ }dx\\ &=3+\int_0^6\dfrac{\sqrt{4x+1}}{2}\text{ }dx \end{aligned}$ Make a $u\text{-substitution}$ to solve the integral. Let $u=4x+1.$ Then $du=4dx.$ $\begin{aligned} \int_0^6\dfrac{\sqrt{4x+1}}{2}\text{ }dx&=\dfrac{1}{4}\int_1^{25}\dfrac{\sqrt{u}}{2}\text{ }du\\ &=\dfrac{1}{8}\int_1^{25}\sqrt{u}\text{ }du\\ &=\dfrac{1}{8}\times\left.\dfrac{2}{3}\sqrt{u^3}\right|^{25}_1\\ &=\dfrac{1}{12}\times\left.\sqrt{u^3}\right|^{25}_1\\ &=\dfrac{1}{12}\times(125-1)\\ &=\dfrac{124}{12}\\ &=\dfrac{31}{3} \end{aligned}$ Adding back in the $3$ from earlier, $3+\frac{31}{3}=\frac{40}{3}.$ Thus, $A=40$ and $B=3,$ so $A+B=\boxed{43}$

You could have ignored the quadratic by

$\left( \frac { d }{ dy } \right) { y }^{ 2 }-y=x\left( \frac { d }{ dy } \right) \longrightarrow dx=dy(2y-1)$

Thus

$\int _{ 0 }^{ 6 }{ ydx } \Longrightarrow \int _{ 1 }^{ 3 }{ y(2y-1)dy\longrightarrow } { | }_{ 1 }^{ 3 }\quad \frac { { 2y }^{ 3 } }{ 3 } -\frac { { y }^{ 2 } }{ 2 } =\frac { 40 }{ 3 }$

Beakal Tiliksew - 7 years, 1 month ago

Good one

Pratik Kulkarni - 7 years, 1 month ago

This method will give 4 different combinations of upper and lower limits. (3,0) (-2,0) (3,1) (-2,1) Out of these 4, 3 are giving positive result. Which is going to have 3 possible solutions of the problem

keshavendra singh - 7 years, 1 month ago

why does it change from 0 and 6 to 3 and 1? I understand the 3, but how do you get the 1?

Shashvat Shukla - 7 years, 1 month ago

well, when we made a U-substitution in this case a y substitution of ${ y }^{ 2 }-y=x$ i plugged in the value of upper and lower limit of x, to get the new value of $y$ Plugging the upper limit ${ y }^{ 2 }-y=6\quad \Longrightarrow y=3\\ \\$ plugging the lower limit

${ y }^{ 2 }-y=0\quad \Longrightarrow y=1$

Beakal Tiliksew - 7 years, 1 month ago

@Beakal Tiliksew – what about y=0?

Shashvat Shukla - 7 years, 1 month ago

@Trevor B. I did the same thing as @Beakal Tiliksew but used $0$ instead of $1$ as my lower limit of integration since it was more intuitive..It seems that both $1$ and $0$ can be the value of the infinite nested radical of $0$ as they both satisfy $y^2=x+y$ for $x=0$ .

Thaddeus Abiy - 7 years, 1 month ago

You have to be careful to ensure that you chose the correct path when you do a variable substitution. This is less of an issue when you are integrating in 1 dimension, though you have to be careful with substitutions like $u = \frac{1}{x}$ .

Calvin Lin Staff - 7 years, 1 month ago

When one makes a u-substitution all the old instances of the variable must change, as we have introduced a new function, Much like negative time, 0 is in this case is an extraneous solution, So i guess the @Trevor B. goes around this ambiguity

Beakal Tiliksew - 7 years, 1 month ago

I knew that you could do it this way, but I'm not 100% sure as to how to determine what the limits are coming from the substitution. For example, on the problem I submitted yesterday, my method was to substitute the whole thing in a $u\text{-substitution},$ solve for $dx$ in terms of $du,$ and find the indefinite integral and plug back in the original limits.

Trevor B. - 7 years, 1 month ago

I do not see why $0$ has to be an extraneous solution.After running a few computations on my computer it seems that the infinite nested radical of $0$ does seem to approach $1$ ,but that does not mean it is 1 at 0.That would mean incorrectly assuming the function is continuous at $x=0$ which it doesn't seem to be. This plot should demonstrate what I mean.

Thaddeus Abiy - 7 years, 1 month ago

@Thaddeus Abiy – Indeed, the function $\sqrt{x + \sqrt{x + \sqrt{x + \ldots}}}$ is discontinuous at $x = 0$ , having a value of $0$ . From the right side, the limit is $1$ , while from the left side, the limit doesn't exist (because the function is also not defined). However, you should take the value $1$ as the lower limit of the integration, because it's the value of the right limit.

Ivan Koswara - 7 years, 1 month ago

@Ivan Koswara – That makes sense. Thanks.

Thaddeus Abiy - 7 years, 1 month ago

i did the same way why is my answer different hey,, AS it is a quadratic the answer 27 is also possible 43 and 27 is the answer

Rahul Sreedhar - 7 years, 1 month ago

could u please tell me formula for integrating sq.root of u

Thala Vijay - 7 years, 1 month ago

$\displaystyle\int\sqrt{u}\text{ }du=\displaystyle\int u^{\frac{1}{2}}\text{ }du=\dfrac{1}{\frac{3}{2}}u^{\frac{1}{2}+1}+C=\dfrac{2}{3}u^{\frac{3}{2}}+C$

Trevor B. - 7 years, 1 month ago

Good one,upvoted.Would have been better had u explained why u neglected the other root(in considering the other root, A/B<0 contradictory to the given conditions of the problem).

rajdeep brahma - 4 years, 1 month ago

I programmed in C to find out the result, and I was right haha :))

ナルトウズマキ - 7 years, 1 month ago

Finn Hulse
Apr 17, 2014

Alright, I'm pretty much doing the same thing as @Trevor B. , except I'm going to just show that there is another solution but it's negative. Here we go. First start off by setting $\sqrt(x+\sqrt(x...))=y$ . To solve in terms of $x$ , simply square both sides to get $x+y=y^2$ . We can set up the quadratic function, but unlike Trevor's solution, I will consider what happens if you use $\pm$ instead of just $+$ . When you do this, you get $\frac{1\pm \sqrt(4x+1)}{2}$ . The reason that there are two different cases for the graph is that it's a parabola with a horizontal axis of symmetry which isn't a function itself. So we have two cases for functions:

Integrate $\frac{1-\sqrt(4x+1)}{2}$ which is $-\frac{22}{7}$ . This obviously cannot be the answer, but it could be a clue as to why $\pi$ isn't equal to $\frac{22}{7}$ . @Calvin Lin you should check it out! Anyways, next case.

We integrate $\frac{+\sqrt(4x+1)}{2}$ . This produces $\frac{40}{3}$ , which is positive, and thus $a+b=\boxed{43}$ . And we're finished. :D

You have a bit of a problem here @Finn Hulse . You are saying that when you expand $y=\sqrt{x+\sqrt{x+\sqrt{x+\ldots}}},$ you will get to $y^2-y-x=0.$ This is correct. But here's the mistake.

Suppose you are trying to find $\sqrt{6+\sqrt{6+\sqrt{6+\ldots}}}.$ $\begin{aligned} y&=\sqrt{6+\sqrt{6+\sqrt{6+\ldots}}}\\ y&=\sqrt{6+y}\\ y^2&=6+y\\ y^2-y-6&=0\\ (y+2)(y-3)&=0 \end{aligned}$

You are saying that the above can have a negative solution, but it won't work in the integral. That isn't true. Remember that $\sqrt{k}$ is non-negative for all non-negative $k.$ The negative solution you could get is extraneous. $\sqrt{4}\neq-2.$ That's why I omitted the possibility of a negative solution in the quadratic formula.

You say that because $\displaystyle\int_0^6\dfrac{1-\sqrt{4x+1}}{2}\text{ }dx=\dfrac{-22}{7},$ $\pi$ is not equal to $\frac{22}{7}.$ Can you explain this please? The only way to get $\pi$ with square roots (that I can remember as of now) is finding $\sqrt{6\zeta(2)}$

Trevor B. - 7 years, 1 month ago

Uh... I'm pretty sure I was just splitting the parabola formed into two respective functions and integrating for each. It does matter if you're graphing it correctly.

Finn Hulse - 7 years, 1 month ago

What I'm saying is that you can't say there is a negative solution. The solution is the graph of $y^2-y=x$ in the first quadrant, or you'd have imaginary or extraneous solutions.

Can you please explain the thing about $\pi$ please? To me it just seems like a coincidence.

Trevor B. - 7 years, 1 month ago

@Trevor B. – Okay, in general, calculus allows you to integrate complex/imaginary functions on the real coordinate system. For example, the line $x=y^2$ looks like a parabola on its side. If you're asked to integrate, both cases are considered. About the $\pi$ thing. @Calvin Lin was looking for a proof that $\pi$ does not equal $\frac{22}{7}$ . I wondered if somehow the fact that that was the imaginary integral of the function could mean something and lead to a possible proof.

Finn Hulse - 7 years, 1 month ago

let t = under root x+....... and so on (i.e. whatever function we have to integrate). then, t 2 = x + t .
implies t
2 - t = x...... hence (dx/dt) = 2t - 1. as such...... we may put dx = dt (2t-1). now this would yield
I (the required integral) =( (integration of) t
(2t-1)) dt = integration of 2((t) 2) - t = (2/3) t *3 - (t 2)/2. proceeding further I got I= 126. whats wrong with my approach please tell me!

Mayank Holmes - 7 years, 1 month ago

why pi is not equal to 22/7 is what makes your solution nique

rajdeep brahma - 4 years, 1 month ago

Jin Young Hwang
Apr 26, 2014

I think the first thing to solve the problem is to show that $\sqrt{x+\sqrt{x+\sqrt{x+\cdots}}}$ exists. See here .

That isn't very difficult. It is easy to prove that the function is monotonically increasing and is convergent at $0$ and $6.$

Trevor B. - 7 years, 1 month ago

Super Rads

The answer is 43.

3 solutions

0 pending reports