Superconducting Loop
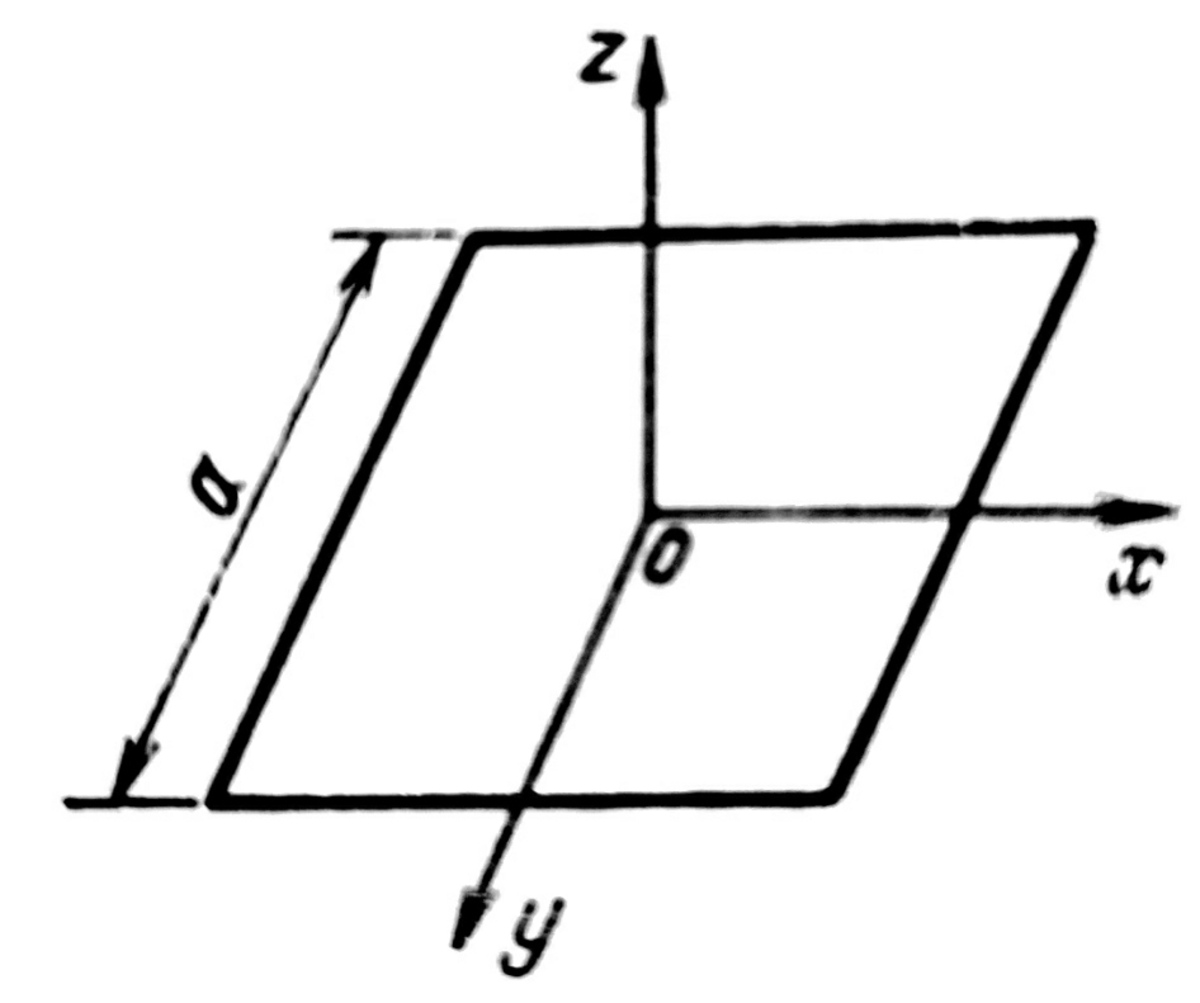
A quadratic undeformable superconducting loop of mass
m
and side
a
lies in a horizontal plane in a nonuniform magnetic field whose induction varies in space according to the law
B
x
=
−
α
x
B
y
=
0
B
z
=
α
z
+
B
0
The inductance of the loop is
L
.
At the initial moment, the centre of the loop coincides with the origin
O
, and its sides are parallel to the
x
and
y
axes. The current in the loop is zero, and it is released.
Where will it be ( z coordinate ) in time t after the beginning of the motion ?
Answer comes in the form of z = a β α γ m g L ( ϕ + cos ( L m a γ α t ) )
Type your answer as β + γ + ϕ = ?
Details and Assumptions
1)
β
,
γ
,
ϕ
all are integers.
2)
Gravity is acting in
−
z
direction.
The problem is not original.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath
Accurate solution.
BTW even disregarding sign convention how you reached the correct answer??
Log in to reply
If you choose a wrong sign convention, the general solution will have the form:
A e ω t + B e − ω t + C
A,B and C are constants. Since the form of the solution is given, I already knew what the final differential equation should look like. I took a shortcut.
Log in to reply
@Karan Chatrath Sir enjoy the previous problem also, and I will be happy if you upgrade it.
I also disregarded the sign convention at first and then just fixed it at the end to give me the right physics.
from the circuit equation, it can be shown that the current is linear with z. writing the energy equation, the inductor energy can be written as if it were that of a spring. we determine the effective spring constant, and the rest of the analysis becomes that of a spring mass system under gravity.
@Karan Chatrath
3
.
1
0
3
(
b
)
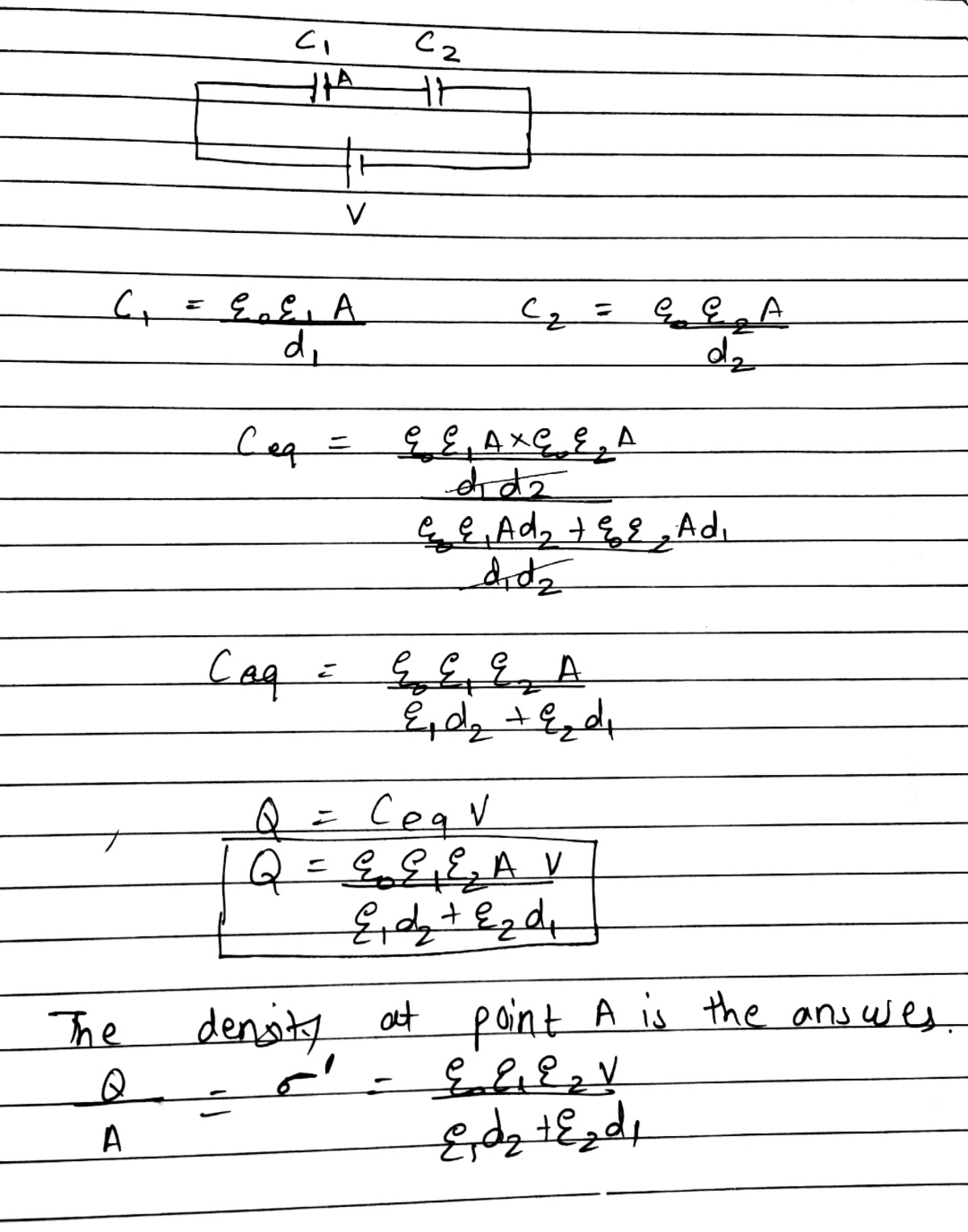
 Here is my solution which is giving wrong answer
Here is my solution which is giving wrong answer
Steven sir has posted the solution of this problem in discussion section also.
But that was different method, I just want to know what is wrong in my method.
Thanks in advance.
You have found the charge density at either plate of the capacitor. My result is the bound charge density at the dielectric interface. They are different things.
Log in to reply
@Steven Chase sir please check your last 24 hour notifications, I have commented you on that place where we were talking.
@Steven Chase sir i am planning to post a mechanics problem right now. Are you ready??
Log in to reply
I am indeed
Log in to reply
@Steven Chase
–
@Steven Chase
Sir it is up now
Sorry for being late.
@Steven Chase
–
@Steven Chase
sir can you please bear the pain to solve this equations.
After solving I think your new problem wedge block and spring can be solved very easily
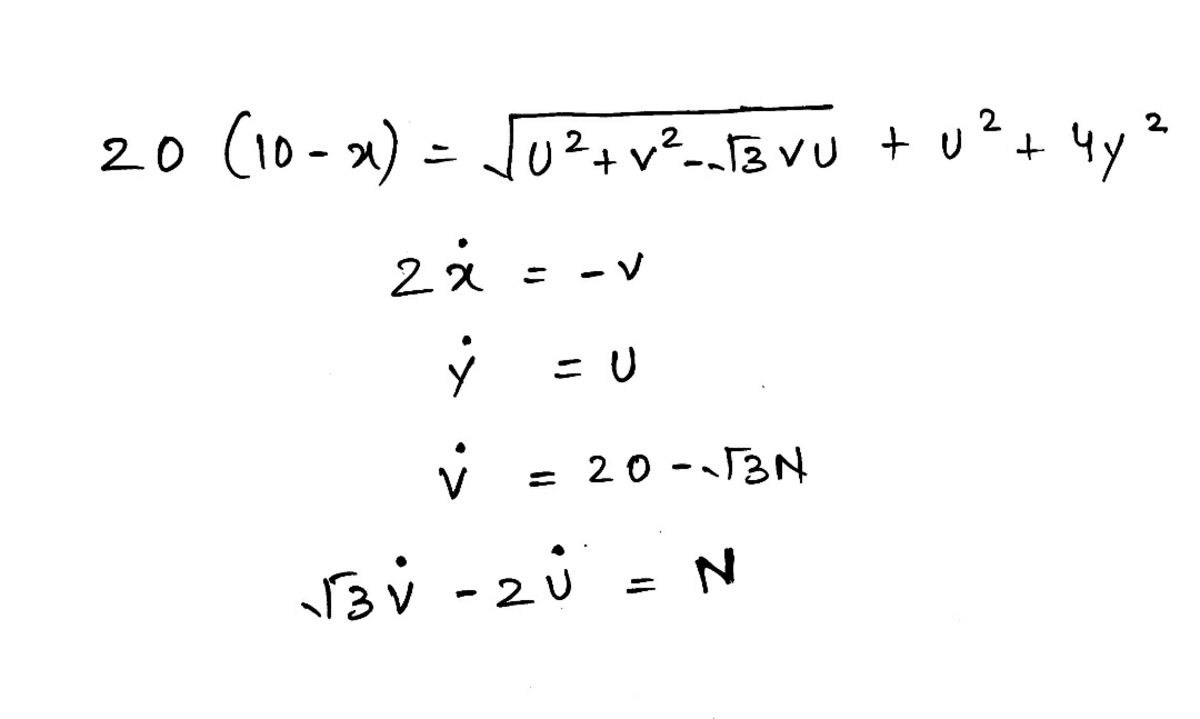
Thanks in advance.
Log in to reply
@A Former Brilliant Member – You can try using code to solve your equations
Log in to reply
@Steven Chase
–
@Steven Chase
sir i don't know how to solve equations using code
My planning is that first I will calculate the time for the block to reach the ground after that, that time will be used to calculate the distance travelled by that wedge, is it possible to do so in code.
If you are free, can you solve using your code.
Then I will be very Happy.
Thanks in advance
Disregarding any sign conventions:
FLux through the loop at any instant:
ϕ = a 2 B z
Therefore magnitude of induced EMF:
∣ ϕ ˙ ∣ = a 2 α z ˙
Using Kirchoff's voltage law:
a 2 α z ˙ = L I ˙
When t = 0 , z = 0 and I = 0 . Integrating:
a 2 α z = L I
At any instant of time, the total magnetic force along the vertical ( F = I a B x applied for side of the loop and added):
F B = − α a 2 I
Newton's second law:
m z ¨ = F B − m g
Simplifying: z ¨ + m L α 2 a 4 z = − g
z ( 0 ) = z ˙ ( 0 ) = 0
General solution:
z = A cos ( m L α a 2 t ) + B sin ( m L α a 2 t ) − α 2 a 4 m L g
Applying initial conditions and solving for A and B :
z = α 2 a 4 m L g ( − 1 + cos ( m L α a 2 t ) )