SuperHero Circles
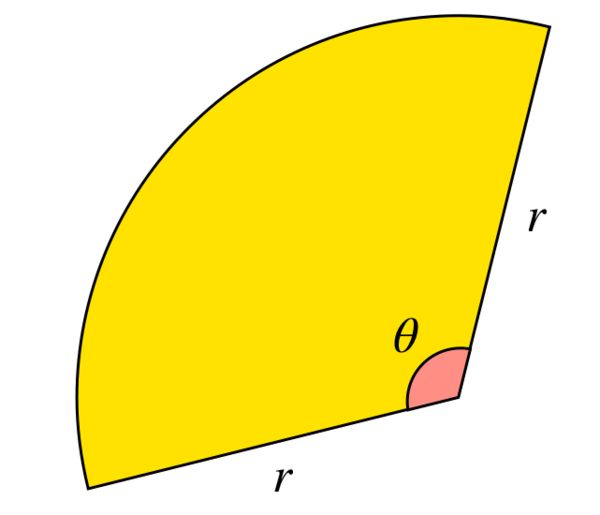 How many sectors with radius
r
∈
N
and real angle
θ
∈
[
2
π
,
2
3
π
]
exist, such that:
How many sectors with radius
r
∈
N
and real angle
θ
∈
[
2
π
,
2
3
π
]
exist, such that:
Perimeter = Area
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I got this correct at one go... ;)
Assuming a constraint r > 0 to exclude the degenerate case...
The area of the sector is A = 2 θ r 2 .
The perimeter is P = 2 r + r θ .
Set A = P : 2 θ r 2 = 2 r + r θ
Divide both sides by (non-zero) r and multiply by 2 :
r θ = 4 + 2 θ , so r = θ 4 + 2 .
We are told that
r
is an integer, thus,
θ
4
must be an integer.
The only integral values of
θ
4
in the range from
2
π
to
2
3
π
are found when
θ
=
2
,
4
.
Thus there are exactly two solutions. ( θ , r ) = ( 2 , 4 ) and ( θ , r ) = ( 4 , 3 )
For all positive integers θ , the total number of such circles is 3 , corresponding to θ = 1 , 2 , 4
Log in to reply
θ = 1 is less than 2 π and can be discarded as out of range.
Log in to reply
I know that. I'm just telling about the total number of supercircles possible.
Log in to reply
@A Former Brilliant Member – Well if you are saying that, then there are infinitely many Superhero circles. You can picture it like this, The radius increases and the angle starts decreasing. But since the problem has specified the range, we only get two solutions
Log in to reply
@Mahdi Raza – The radius increases and the angle starts decreasing... but maintaining it's integer restriction. Of course, the angle can't be zero, as then the radius becomes infinite, loosing it's integer attribute. So in all, there are only three circles, with ( r , θ ) values ( 6 , 1 ), ( 4 , 2 ) and ( 3 , 4 )
Log in to reply
@A Former Brilliant Member – There is no restriction on angle θ . I still don't get your point, I can list infinite solutions for this problem because its just a diophantine equation with θ and r. Ex, r = 10, θ = π 9 0 and r = 12, θ = π 7 2 ........
Log in to reply
@Mahdi Raza – First, at θ = π 9 0 , r = 2 + θ 4 = 1 0 . Second, if I am not mistaken, in the original version of the problem, the word "real" was absent before "angle θ ",from which the obvious impression of "integer angle" emerged.
Log in to reply
@A Former Brilliant Member – I edited the semantics if at all it was confusing because when read, it read that θ was also an integer. Also, r and θ should be independent if I am not wrong because now I am getting confused about my own problem.
Log in to reply
@Mahdi Raza
–

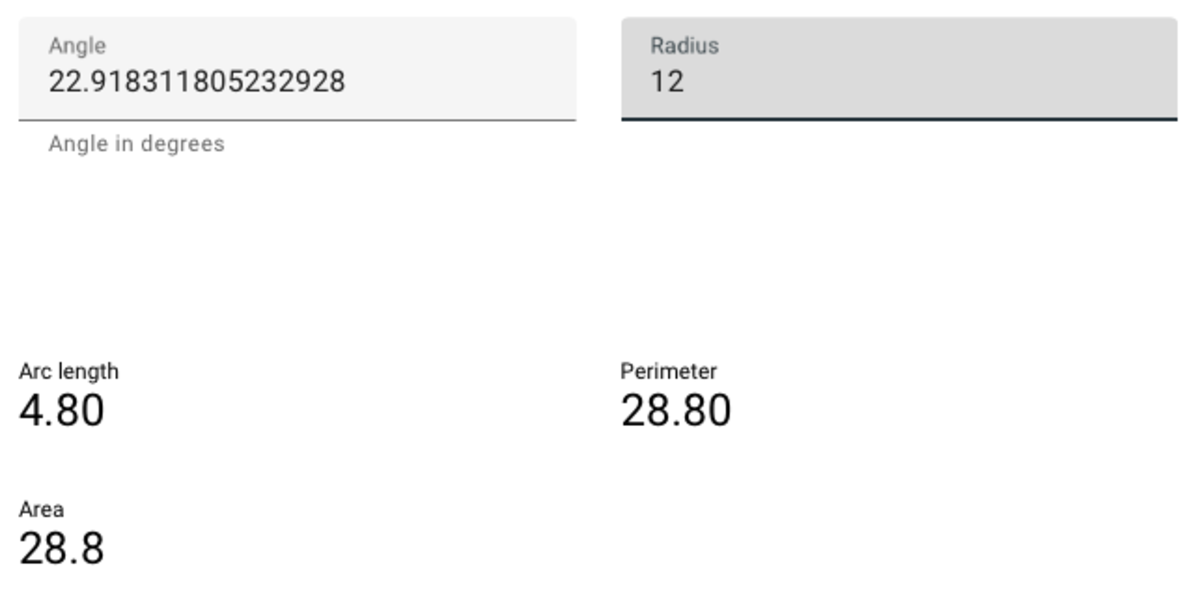 Here you go, integer radius but not angle and satisfying the conditions. I am just trying to say that there exist infinitely many such sectors, but according to the question only 2 are in the range to be considered as valid
Here you go, integer radius but not angle and satisfying the conditions. I am just trying to say that there exist infinitely many such sectors, but according to the question only 2 are in the range to be considered as valid
It said r must be an integer. The same was not said of theta. There are plenty of non-integer values of theta that satisfy 4/theta in Z. Just not in this range.
For example, theta = 1/2. Theta = 4/7. Basically any value theta = 4/n, where n is an integer.
If r is the radius and theta is the central angle, we have Perimeter = 2 r + r (theta). Also, Area = (.5) r r (theta). Setting these equal and solving for theta gives: theta = 4/(r-2). The restriction on theta means (Pi) / 2 < 4/(r-2) < 3 Pi/2, or Pi < 8/(r-2) < 3*Pi. Substituting integral values of r into the middle expression shows that r = 3 and r = 4 both satisfy the inequality. The fact that the middle expression is decreasing with increasing r means that these can be the only two solutions.
@Mahdi Raza , I guess you should mention that r > 0 because at r = 0 (integer), both area and perimeter are 0 so there can be 3 solutions
Area of the sector is given by A = 2 θ r 2 and its perimeter p = θ r + 2 r . When A = p , we have:
2 θ r 2 ⟹ r = θ r + 2 r = 2 + θ 4 Multiply both sides by θ r 2
For θ ∈ [ 2 π , 2 3 π ] , integer values of θ are 2 , 3 , and 4 . For r to be an integer, θ can only be 2 and 4 , then r = 4 and 3 respectively. Therefore there are only 2 solutions.