Surface area of a cut cone
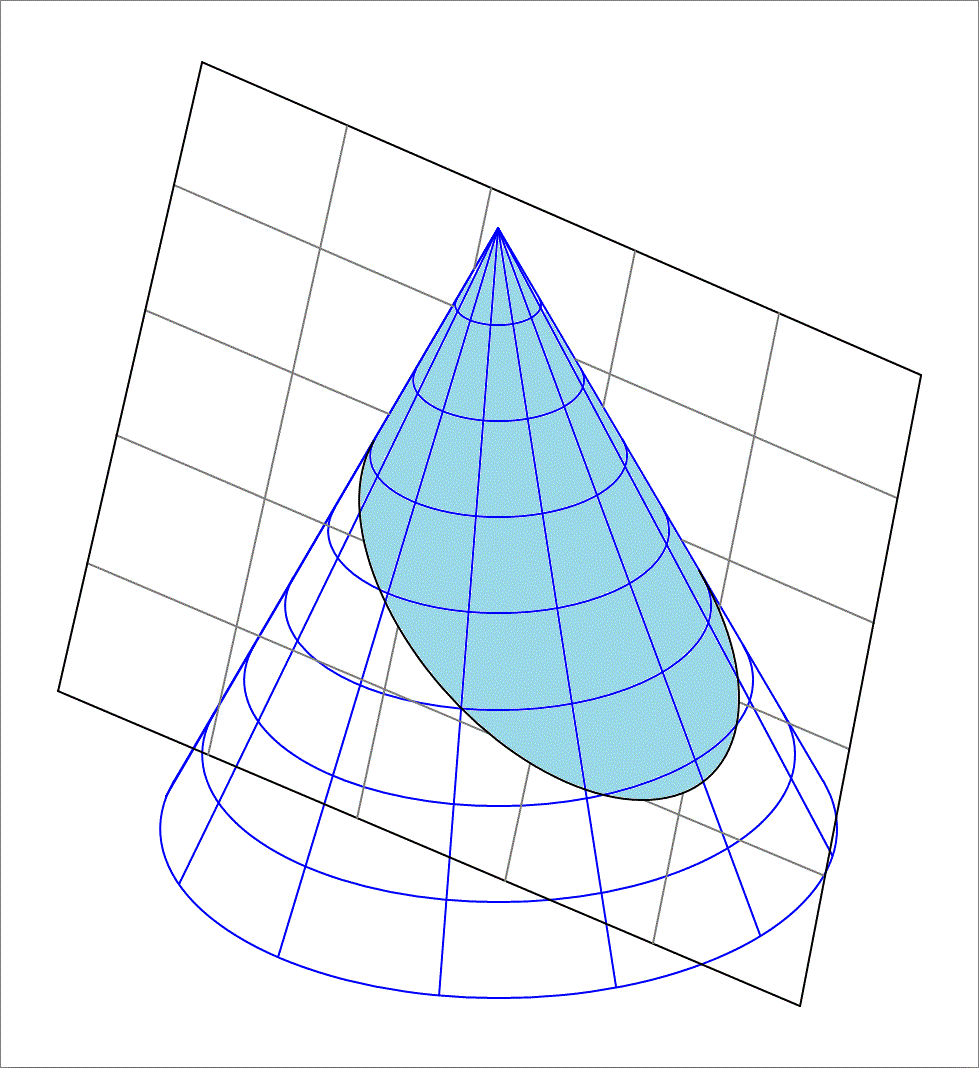
You have a right circular cone with base radius 1 0 and height 2 0 . The base is centered at the origin of the x y z reference frame, with its axis extending along the z axis, and apex at ( 0 , 0 , 2 0 ) . Now you pass a cutting plane through the cone. The cutting plane passes through the point ( 0 , 0 , 1 0 ) and its normal vector is n = ( 2 , 3 , 5 ) . Find the surface area of the cone that is above the cutting plane (shaded in light blue in the above figure). You may need the following formulas for the semi-minor and semi-major axes lengths of the elliptical section resulting from the cut. (Note that the area of this ellipse is not part of the required surface area).
Semi-minor axis length = a = 1 − sin 2 ϕ sec 2 θ z 0 tan θ cos ϕ
Semi-major axis length = b = 1 − sin 2 ϕ sec 2 θ z 0 tan θ cos ϕ
Where z 0 is the distance between the apex of the cone and the point of intersection between the cutting plane and the axis, θ is the semi-vertical angle of the cone, i.e. the angle between the axis of the cone and its surface., and ϕ is the acute angle between the normal vector of cutting plane and the axis of the cone.
These formulas are derived in the solution of this problem
The answer is 216.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks to GeoGebra, here's a picture of the unrolled net showing the intersection line:
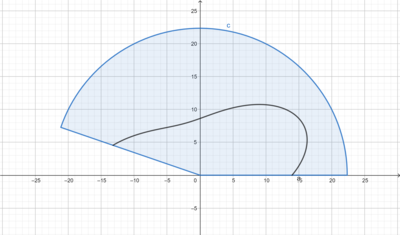
If anyone fancies getting arts and craftsy, I'd be interested to know how it looks if you cut it out and fold it!
Using the formulas given, we have,
θ = tan − 1 ( 2 1 ) , ϕ = cos − 1 3 8 5 , and z 0 = 1 0
Therefore, the lengths of the semi-axes are,
Semi-minor axis length = a = 5 . 3 6 0 5 6 2 6 7 4 , and Semi-major axis length = b = 7 . 0 8 5 5 3 3 3 3 7
Hence, the area of the elliptical section is A = π a b = 1 1 9 . 3 2 5 3 7 1 8
Now comes the trick of this problem. We will project the ellipse area onto the x y plane. The area of the projected elliptical section is simply
A Projected = A cos ϕ = 9 6 . 7 8 5 6 5 6 9 9
And finally, we note that projecting the area of the conical surface (which is above the cutting plane) onto the x y plane results in the same elliptical region in the x y plane as the elliptical region resulting from projecting the elliptical conic section (the one that is on the cutting plane as well). Thus if S is the surface area then
S sin θ = A Projected
Therefore, S = sin θ A cos ϕ = 2 1 6 . 4 1 9 3 0 . . . ≈ 2 1 6 . 4
That's a really nice approach. I love the idea of projecting it down to a plane and then back to the cone!
Log in to reply
Oh, by the way, another way of finding the projection down to the x y -plane would be to eliminate z from the equations; ie from the plane 2 x + 3 y + 5 z = 5 0 we get z = 1 0 − 5 2 x + 3 y and plugging into the equation for the cone x 2 + y 2 = 4 ( 2 0 − z ) 2 we get (after tidying) 9 6 x 2 − 1 2 x y − 2 0 0 x + 9 1 y 2 − 3 0 0 y − 2 5 0 0 = 0 ...which I know you know how to deal with!
Log in to reply
Thanks for your helpful remark.
Log in to reply
@Hosam Hajjir – I also like that we've both solved this by flattening the cone, but in different ways. Thanks for a fun problem (in fact, a lot of fun problems - you've been very active lately!)
Log in to reply
@Chris Lewis – Actually, I did not flatten the cone. I just projected the original portion of the cone that is above the cutting plane onto the x y plane, and noticed that the projection results in the same elliptical region as the projection of conic section (which lies on the cutting plane) onto the x y , which is plain to see. The key observation here is that an area element on the cone lateral surface of area d A has a projected area of d A sin θ .
To make the algebra neater, translate everything by − 2 0 in the z -direction, so that the cone's apex is at O and the plane passes through 0 , 0 , − 1 0 .
The equation of the plane is 2 x + 3 y + 5 z = − 5 0 . In cylindrical coordinates, this is 2 r cos θ + 3 r sin θ + 5 z = 5 0
The equation of the cone is r 2 = 4 z 2 ; bearing in mind we're interested in negative z , this becomes 2 r + z = 0
Solving these, we find r = 1 0 − 3 sin θ − 2 cos θ 5 0 z = − 1 0 − 3 sin θ − 2 cos θ 1 0 0
The distance of this point from O is given by R = 1 0 − 3 sin θ − 2 cos θ 5 0 5
In order to find the area, we need to evaluate A = k ∫ 0 2 π 2 1 R 2 d θ
Note this is similar to the usual area integral in polar coordinates, but with a constant, k . We're approximating the area by isosceles triangles with equal sides R ( θ - the same as in polars - but we need to convert from θ (which measures around the base of the cone) to the angle ϕ = k θ at the apex of the cone.
To find this k , just unroll the cone; its net is a sector of a circle, with radius equal to the slant height of the cone (which is 1 0 5 ). The circumference of the base of the cone is 2 0 π ; so this is the arc length of its net. Hence the angle of the sector is 1 0 5 2 0 π = 5 2 π and we need k = 5 1 .
Putting everything together, A = 2 5 1 ∫ 0 2 π ( 1 0 − 3 sin θ − 2 cos θ ) 2 1 2 5 0 0 d θ = 8 7 8 7 2 5 0 0 0 5 π ≈ 2 1 6 . 4 1 9 3