Sweet Red Fish
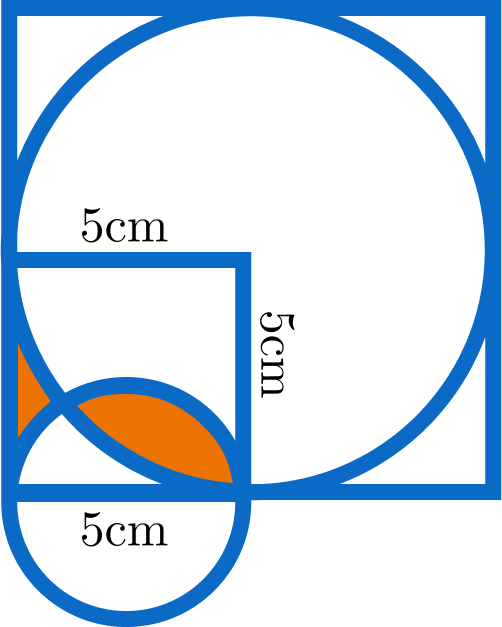
The figure above shows that a large circle with radius 5 cm is inscribed in a square and another circle with diameter 5 cm is only half inside that square.
Calculate the area of the shaded region (colored red) in the figure. Give your answer in cm 2 to three decimal places.
Details and Assumptions :
- You may use the approximation π = 3 . 1 4 1 5 9 and sin − 1 ( 5 4 ) = 0 . 9 2 7 2 9 .
The answer is 7.5692.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
@Arpit Mishra Nice problem. It was a challenge to solve this without resorting to calculus. :)
Log in to reply
I also first tried it by doing it using coordinate geometry but then it was getting a tedious work . I liked your solution using coordinate geometry! Nice solution!
I have to say this is the most tedious geometry problem I have seen for a long time.... But its an amazing problem!
Very nice solution I tried it with pure geometry but was unable to do so
we can solve by using integration ,
[ Integration of ( sqrt(5x-x^2) + sqrt(10x-x^2) -5 )dx from x=1 to x=5 ] + [ Integration of ( -sqrt(10x-x^2) +5 -sqrt(5x-x^2) )dx from x=0 to x=1 ]
= 6.011+1.5585 = 7.5695
I found 7.854 , I did as follow:
Can you please spot the mistake .
A r e a o f B i g S q u a r e − B i g C i r c l e : 4 1 0 0 − 2 5 π s i n c e w e w o u l d h a v e 4 e q u a l a r e a s a t t h e 4 c o r n e r s , S m a l l S q u a r e − S m a l l c i r c l e
2 5 − 5 π
Q u a t e r C i r c l e = 4 2 5 π Q u a t e r C i r c l e − S m a l l C i r c l e A n d ∴ 4 2 5 π − 5 π ∴ 2 5 − 5 π − 4 2 5 π − 5 π ⟹ 2 5 − 4 6 5 π 4 1 0 0 − 2 5 π − 2 5 − 4 6 5 π = − 7 0 . 6 8 5 7 7 5 ⋯ ⋯ Ⓢ 2 5 π + Ⓢ = 7 . 8 5 4
Log in to reply
You're taking the area of the small circle as 5 π , where I think it should actually be π ( 2 . 5 ) 2 = 6 . 2 5 π . I think that you are also meaning to use only the area of half of this circle, i.e., 3 . 1 2 5 π . Also, when subtracting the "Quarter circle - small (semi)-circle" value from the "Small square - small (semi)-circle" value, you will actually end up with just the area of the region between the big square and big circle in the lower left corner, which is the same as the first value in your solution.
Log in to reply
Thank you,
My main mission was to find the area of shaded region by doing as follows, I hope it is correct.
- Finding Area : Small Square - Quarter Area of Big Circle --------(i)
- Finding Area : Small Circle (Semi) - Small Square------------------(ii)
-
Area of small square - **Area of both (i) and (ii) will give the area of one of the desired region however the other one is left which. ----------- (a)
-
Area of Semi Circle - Area found (the other Region ) Gives Area of White Region between two Red Regions -----------------(iii)
- Area of Big Square - Area of Big Circle and Divide the answer by 4.
-
Answer - Area from (iii)
-
_Finally ADD the two answers i.e. (iii) + Area found in part (a) gives desire area.
First my math skills suck compared to you guys as I only had basic Geo and trig in high school in the mid 60's. My approach was to find center distance with Pythagorean theorem. Small circle radius divided by the center distance X large circle radius gave me 1/2 chord length. So chord length was 4.472135954999. I also had all the angles. Never did chord area before and looked up chord area formulas and went from there.
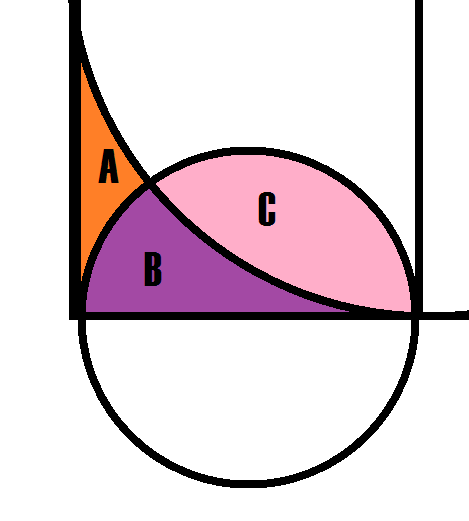
Let A , B , C denote the area of orange, purple, and pink regions respectively. So we want to find A + C
A + C = = = = ( A + B − B ) + ( C + B − B ) ( A + B ) + ( B + C ) − 2 B ( A + B ) + ( B + C ) − 2 ( B + C − C ) ( A + B ) − ( B + C ) + 2 C
A + B is the area quarter of the square minus the area of sector with 9 0 ∘ of the larger circle. So A + B = 5 2 − 4 1 π ⋅ 5 2 = 2 5 − 4 2 5 π
B + C is the area of semicircle of the smaller circle, which means B + C = 2 1 ⋅ π ( 2 5 ) 2 = 8 2 5 π
The radius of the smaller circle is simply 2 5
To solve for C , we first need to find the coordinates of the intersection of the two circles. Apply coordinate geometry: x 2 + y 2 = 5 2 , ( x + 2 5 ) 2 + ( y + 5 ) 2 = ( 2 5 ) 2 solving them simultaneously gives points D ( − 4 , − 3 ) , E ( 0 , − 5 )
Let O 1 , O 2 denote the point of the center of the larger and smaller circle respectively. And denote θ 1 , θ 2 as the measure ∠ E O 1 D , ∠ D O 2 E respectively.
Then, D O 1 = E O 1 = 5 , D O 2 = E O 2 = 2 5 , and D E = 4 2 + 2 2 = 2 0
By Cosine Rule, we have cos θ 1 = 2 ⋅ 5 ⋅ 5 5 2 + 5 2 − 2 0 = 5 3 ⇒ sin θ 1 = 5 4 . Similarly, cos θ 2 = 2 ⋅ ( 2 5 ) ⋅ ( 2 5 ) ( 2 5 ) 2 + ( 2 5 ) − 2 0 = − 5 3 ⇒ sin θ 2 = 5 4 , θ 2 = π − sin − 1 ( 5 4 )
We split C into two parts: one part above line D E , the other below line D E .
For the area above D E denoting as C 1 , it is simply the area of sector D O 2 E minus the area of triangle D O 2 E
C 1 = = 2 1 ⋅ r 2 ( θ 2 − sin θ 2 ) 2 1 ⋅ ( 2 5 ) 2 ( π − sin − 1 ( 5 4 ) − 5 4 )
Likewise, for the area below D E denoting as C 2 , it is the area of sector D O 1 E minus thue area of triangle D O 1 E
C 2 = = 2 1 ⋅ R 2 ( θ 1 − sin θ 1 ) 2 1 ⋅ 5 2 ( sin − 1 ( 5 4 ) − 5 4 )
Add all of them up: ( A + B ) − ( B + C ) + 2 ( C 1 + C 2 ) gives 7 . 5 6 9
Sorry for the duplication, (although we did take slightly different approaches to find the area of B ). I noticed that you had at first used calculus, so I thought it would be worth providing a non-calculus method. But when I (finally) finished my solution I noticed that you had found a non-calculus approach as well.
Anyway, I found this question to be quite a challenge to solve just with geometry. I think that this question should be rated quite a bit higher than the present 130 points.
Log in to reply
No problem at all! I thought this was in calculus, only to realise that it's a geometry problem, so I "geometrify" it.
Log in to reply
What is the area for C and the area for A?
Log in to reply
@Thomas Mauldin – I've shown above that I don't actually need to calculate the area A , I just need to calculate the value of C , which simply C 1 + C 2 as shown at the end.
we can solve by using integration ,
[ Integration of ( sqrt(5x-x^2) + sqrt(10x-x^2) -5 )dx from x=1 to x=5 ] + [ Integration of ( -sqrt(10x-x^2) +5 -sqrt(5x-x^2) )dx from x=0 to x=1 ]
= 6.011+1.5585 = 7.5695
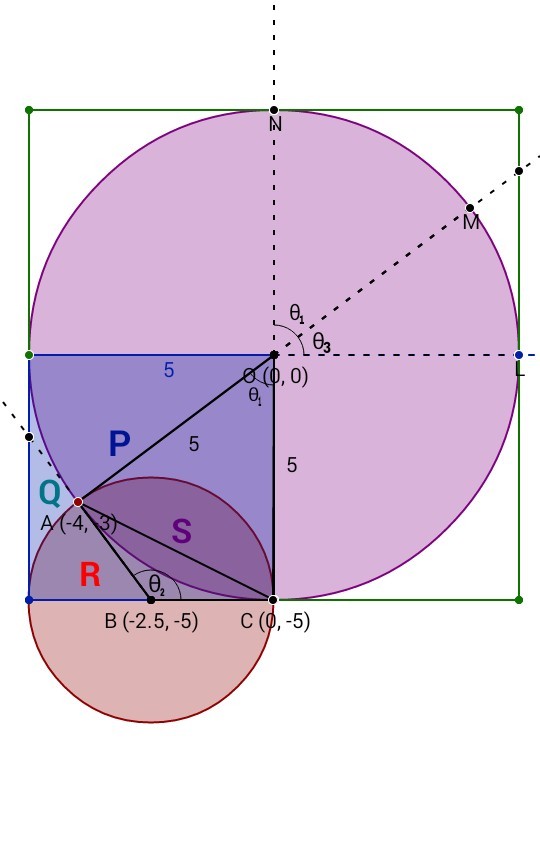
Note: P , Q , R , & S represents the 4 area inside the smaller square.
First of all, take a look at point O, A, B & C, we'll be using only these 4 points in our whole solution. I'll use coordinate system first to get some value. Assume that the center of the bigger circle is at origin O ( 0 , 0 ) & the center of the smaller circle is B ( − 2 . 5 , − 5 ) . Then their respective equations will be, x 2 + y 2 = 5 2 ( x + 2 . 5 ) 2 + ( y + 5 ) 2 = 2 . 5 2 Solving them we get the coordinates of, A ≡ ( − 4 , − 3 ) C ≡ ( 0 , − 5 ) From the slope of line AB we get, tan θ 2 = − 1 . 5 2 ⇒ θ 2 = tan − 1 ( − 3 4 ) = sin − 1 5 4 Similarly, from slope of line AO we get, θ 3 = tan − 1 ( 4 3 ) ∴ θ 1 = 2 π − θ 3 = 2 π − tan − 1 4 3 = sin − 1 5 4 Now, let's divide area S by segment AC into 2 parts named S 1 & S 2 :
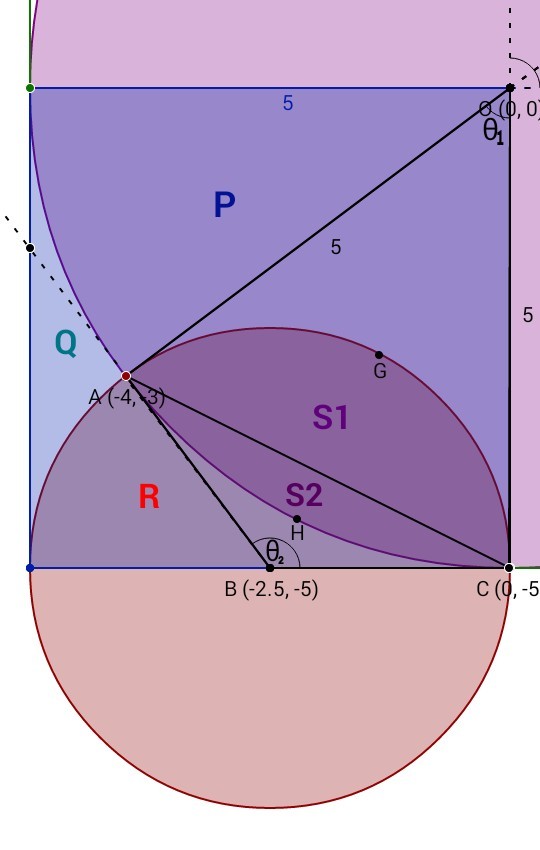
Then area of, S 1 = Sector B A G C − Δ B A C = 2 ( 2 . 5 ) 2 sin − 1 5 4 − 2 1 × 2 . 5 × 2 . 5 × sin ( sin − 1 5 4 ) = 6 . 9 1 9 7 − 2 . 5 [ In 2nd quadrant, sin − 1 5 4 = 2 . 2 1 4 3 ] = 4 . 4 1 9 7
Similarly, area of, S 2 = Sector O A H C − Δ O A C = 2 5 2 × sin − 1 5 4 − 2 1 × 5 × 5 × sin ( sin − 1 5 4 ) = 1 1 . 5 9 1 2 − 1 0 = 1 . 5 9 1 2 Thus, S = S 1 + S 2 = 4 . 4 1 9 7 + 1 . 5 9 1 2 = 6 . 0 1 0 9
Now, area of R is, Area of the small semicircle − S = 2 π × ( 2 . 5 ) 2 − 6 . 0 1 0 9 = 3 . 8 0 6 6
And area of, Q + R = Area of the smaller square − Area of the big quartercirle = 5 2 − 4 π × 5 2 = 5 . 3 6 5 So, Q = 5 . 3 6 5 − 3 . 8 0 6 6 = 1 . 5 5 8 4
Aah! Finally, we got the answer, Q + S = 1 . 5 5 8 4 + 6 . 0 1 0 9 = 7 . 5 6 9 3 ≈ 7 . 5 6 9
I found 7.854 , I did as follow:
Can you please spot the mistake .
A r e a o f B i g S q u a r e − B i g C i r c l e : 4 1 0 0 − 2 5 π s i n c e w e w o u l d h a v e 4 e q u a l a r e a s a t t h e 4 c o r n e r s , S m a l l S q u a r e − S m a l l c i r c l e
2 5 − 5 π
Q u a t e r C i r c l e = 4 2 5 π Q u a t e r C i r c l e − S m a l l C i r c l e A n d ∴ 4 2 5 π − 5 π ∴ 2 5 − 5 π − 4 2 5 π − 5 π ⟹ 2 5 − 4 6 5 π 4 1 0 0 − 2 5 π − 2 5 − 4 6 5 π = − 7 0 . 6 8 5 7 7 5 ⋯ ⋯ Ⓢ 2 5 π + Ⓢ = 7 . 8 5 4
Log in to reply
I haven't read your full approach. On your second equation, you have written area of the smaller circle (I assumed it's the semicircle you are talking about) is 5 π which will actually be 8 2 5 π .
See, if that's the problem.
Log in to reply
No, it is the full circle I mean the area of Small Circle which is 5 π ,
Log in to reply
@Syed Baqir – That's not 5 π either. That'll be π × ( 2 5 ) 2 = 4 2 5 π .
Log in to reply
@Md Omur Faruque – Yeah , My mission was to do the following,
I hope it is correct.
Finding Area : Small Square - Quarter Area of Big Circle --------(i)
Finding Area : Small Circle (Semi) - Small Square------------------(ii)
Area of small square - **Area of both (i) and (ii) will give the area of one of the
desired region however the other one is left which. ----------- (a)
Area of Semi Circle - Area found (the other Region ) Gives Area of White
Region between two Red Regions -----------------(iii)
Area of Big Square - Area of Big Circle and Divide the answer by 4.
Answer - Area from (iii)
_Finally ADD the two answers i.e. (iii) + Area found in part (a) gives desire area.
Log in to reply
@Syed Baqir – Sorry, I didn't understand your solution. However, I hope you got your answer.
Log in to reply
@Md Omur Faruque – Thanks , I think my method is correct but something is wrong in substitution,
Thanks
For convenience, we will use inches, letting 1 inch = 2.5 cm.
Let A be the area of the right red region, B the left red region, C the top white region, and D the lower white region (all our work will take place in the small square on the lower left.)
We have the obvious equations A + B + C + D = 4 , A + C = π , A + D = π / 2 so A + B = 4 + 2 A − 2 3 π .
Let θ = arcsin ( 5 1 ) = 2 arcsin ( 4 / 5 ) . This is the top angle in the right triangle formed by the center of the small circle and the two right corners of the square.
Considering the "kite" formed by the centers of the two circles and the two points of region A, we find A = (sector of large circle) + (sector of small circle) - (area of kite) = 4 θ + ( π / 2 − θ ) − 2 .
Thus A + B = 4 + 2 A − 2 3 π = 6 θ − 2 π ≈ 1 . 2 1 1 1 . Converting the result into square centimetres, we have ( 6 θ − 2 π ) ( 2 5 ) 2 ≈ 7 . 5 6 9 3 .
haha classic american
Log in to reply
I'm a Swiss expat in the US, with a strong pro-metric bent. But I'm not dogmatic: In this particular case, it seemed easier to deal with 2 and 1 than with the numbers 5 and 2.5 ;)
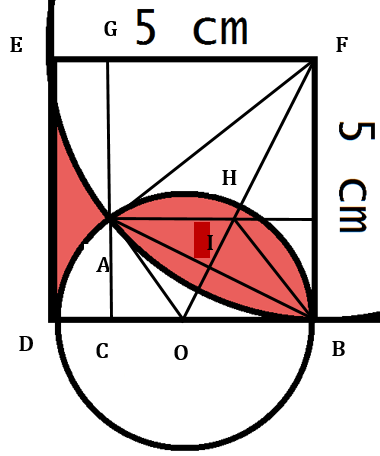
Let O be the center of the smaller circle, A be the upper intersection of both circles, and AH be the line parallel to DB.
△AFB and △ABC are isosceles triangles, which share the same base AB. Thus, the line bisecting these triangles in halves will be perpendicular to AB, also bisecting the segment at point I: that line is OF.
Since AH // OB and AI = IB, △AHI is identical to △OIB as they have all the same angles with at least one equal side. Consequently, △AIO is identical to △HIB, and AO = OB = HB = BA.
Therefore, ⎕AHBC is a rhombus.
Let ∠IBO = 𝜭. △IBO is a right-angled triangle, so ∠IOB = 90 ̊ - 𝜭.
Now considering △FOB, which is also a right-angled triangle, since ∠FOB = 90 ̊ - 𝜭, ∠OFB = 𝜭.
Thus tan 𝜭 = 2.5/5 = ½.
In other words, (sin 𝜭)/(cos 𝜭) = ½.
cos 𝜭 = 2(sin 𝜭)
(cos 𝜭)^2 = 4(sin 𝜭)^2
1-(sin 𝜭)^2 = 4(sin 𝜭)^2
(sin 𝜭)^2 = 1/5.
sin 𝜭 = 1/√5 ; cos 𝜭 = 2/√5
Since ⎕AHBC is a rhombus, its diagonals will bisect all its angles in halves. Thus, ∠IBO = ∠IBH = 𝜭, which means ∠OBH = 2𝜭.
And because AO // HB, ∠AOC = ∠OBH = 2𝜭.
Now applying this to △AOC,
sin ∠AOC = sin 2𝜭 = AC/2.5
sin 2𝜭 = 2(sin 𝜭)(cos𝜭) = 2(1/√5 ) (2/√5) = 4/5
So AC = 2.5(4/5) = 2.
Now we get AG = 3, and using Pythagorean theorem for △AGF, we’ll get:
(AF)^2 = (AG)^2 + (GF)^2
5^2 = 3^2 + (GF)^2
GF = 4
Notice that cos ∠GFA = GF/AF = 4/5 = sin 2𝜭.
That means ∠GFA = 90 ̊ - 2𝜭.
Then we can calculate the total shaded area by working out one portion at a time.
First, we formulate the “fish tail” part: Portion EAD “tail” = ⎕EGDC – Portion EGA – Portion ADC
Then, we formulate the “fish body” part: Portion AB “Body” = Portion GABF + Portion ABC - ⎕GCBF
= (Portion EFB – Portion EGA) + (Portion ADB – Portion ADC)- ⎕GCBF
Combining the terms,
the total area = ⎕EGDC - ⎕GCBF + Portion EFB – 2(Portion EGA) + Portion ADB – 2(Portion ADC)
⎕EGDC = (1)(5) = 5
⎕GCBF = (4)(5) = 20
Portion EFB = (1/4)(π)(5^2) = 6.25 π ≈19.6349
2(Portion EGA) = 2(Portion EFA - △GAF)
= 2[((π/2-2ϴ)/2π)(π)(5^2) – (1/2)(3)(4)]
(converting 90 ̊ - 2𝜭 to radian mode)
= (π/2-2ϴ)(25) – 12
(sin 2𝜭 = 4/5, so 2𝜭 = arcsin (4/5) ≈0.92729)
≈ (π/2-0.92729)(25) – 12
≈4.087625
Portion ADB = (1/2)(π)(2.5^2) = 3.125 π ≈9.8175
2(Portion ADC) = 2(Portion ADO – △ACO)
= 2[(2𝜭/2 π)( π)(2.5^2) – (1/2)(2)(1.5)]
≈ (0.92729)(6.25) – 3
≈ 2.79556
So the shaded area = 5 – 20 + 19.6349 - 4.087625 + 9.8175 - 2.79556 ≈ 7.569
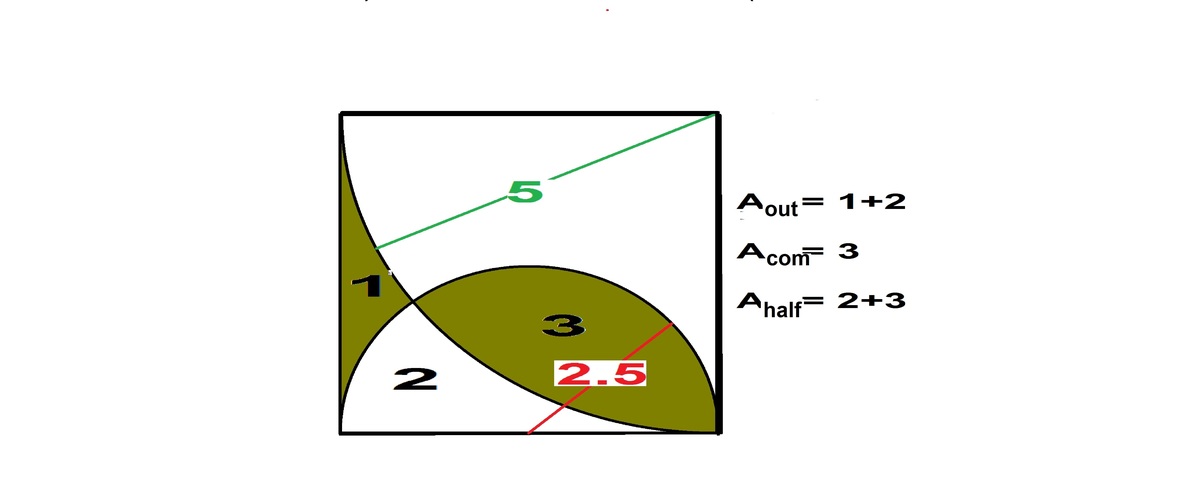
Full geometrical solution I have written has vanished!!!!! I am rewriting the solution. A circle radius R and a segment, central angle 2 θ h a s a n a r e a A s e g . A s e g = A s e c t , i t s s e c t o r a r e a − A t r i , Δ a r e a f o r m e d b y t h e c h o r d a n d i t s b o u n d i n g r a d i i . ∴ A s e g = A s e c t − A t r i = R 2 ( θ − S i n θ ∗ C o s θ ) . . ( 1 ) Here, central distance D, is also the hypotenuse of the right angled triangle with the two radii as legs. ∴ D 2 = 5 2 + 2 . 5 2 a n d D = 2 . 5 5 . ⟹ θ 5 = C o s − 1 5 2 , θ 2 . 5 = C o s − 1 5 1 , t h i s g i v e s S i n s a n d C o s e s . ∴ the COMMON area of the intersecting circles, is A c o m f r o m ( 1 ) i s : − A s e g 5 + A s e g 2 . 5 = 5 2 ( θ 5 − S i n θ 5 ∗ C o s θ 5 ) + 2 . 5 2 ( θ 2 . 5 − S i n θ 2 . 5 ∗ C o s θ 2 . 5 ) ∴ A c o m = 6 . 0 1 1 . . Top half small circle area, A h a l f = 2 π ∗ 2 . 5 2 = 9 . 8 1 7 . Area of bottom left corner within the square without big circle, A o u t = 4 1 0 2 − π ∗ 5 2 = 5 . 3 6 5 . . . L e f t r e d a r e a = A o u t + A c o m − A h a l f . T o t a l = { A o u t + A c o m − A h a l f } + A c o m = 7 . 5 6 9
Take the lower horizontal side of the large square as X-axis
and take the left vertical side of the large square as Y-axis
The equation of the large circle is :
x^2 + y^2 - 10 x - 10 y + 25 = 0
The equation of the small circle is :
x^2 + y^2 - 5 x = 0
These two circles cut each other at two points
The first point is (5 , 0) on the lower horizontal side of the large square ,
the second point is (1 , 2) which is the contact point of the two red regions
Let the area of the large red region be denoted by X
Let the area of the small red region be denoted by Y
Let the part of the small square (above the red regions) be denoted by Z
Then
X + Z = (1/4)(Pi)(5^2) = 19.63495408 ................................................ (1)
Y + Z = 25 - (1/2)(Pi)(2.5^2) = 15.18252296 .....................................(2)
From (1) , (2) we get
X - y = 4.452431122 ....................................................................................(3)
Region X can be divided into two circular segments A , B
Segment A is of radius 5 cm. and angle of measure 0.92729 (in radian )
Segment B is of radius 2.5 cm. and angle of measure (Pi - 0.92729)
Then A = 1.591125 , B = 4.4196875
So
X = A + B = 6.0108
Substituting in (3) we get
Y = 1.558368878
Then
The area of the red regions = X + Y = 7.569
We need to find the area in common between the 2 circles. To do this we think in terms of area of the 2 minor segments. We need the angle so that we can find the area of the 2 segments (0.5(r^2)(x-sin(x)), (x is in radians). Now by the cosine rule we can equate the distance of the chord shared by the 2 circles. root(2.5^2+2.5^2-2(6.25)cos(x))=root(5^2+5^2-2(25)cos(y)). We can then show that y = π - x such that x > y by using theorems from geometry. Using these facts we can show that cos(x) = 3/5. Thus sin(x) = 4/5 (sin(x)>0). Now we can find the area of the intersection by applying the formula twice to get the intersection area as 6.0108697. Now Let A be the set of area contained in the smaller square and B be the set of area of the larger circle such that B is a subset of A and C be the set of area of the smaller circle such that C is a subset of A. We have notB∩C = C - B∩C = (π((5/2)^2)/2)-6.0108697=3.80660733. Now notB∩notC = 25 - 25(π/4)-3.80660733. Hence notB∩notC + B∩C = 25 - 25(π/4)-3.80660733 + 6.0108697 = 7.569
Equation of the large of the large circle +> y=5-sqrt(10x-x^2)
Equation of the small circle= y=sqrt(5x-x^2)
They intersect at point (1,2) and (5,0)
Calculate the area under large circle between x=1 and x=5 Integrate 5-sqrt(10x-x^2) from 1 to 5 = 2.4088
Calculate area under small circle from x=0 to x=1 Integrate sqrt(5x-x^2) from 0 to 1 = 1.3978
Read area (Big circle n Large Circle) = Semi circle -( the two regions calculated above)= ((2.5^2*pi)/2)-3.8066= 6.01087
Second red area= (Square - large circle)/4- two regions calculated above= (100-(pi*25))/4 - 3.8066= 1.55846
Lastly, two red regions area= 6.01087+1.55846=7.56933...

First, we find the point P of intersection of the two circles that correlates with the point where the two shaded regions touch. Letting the lower left corner of the square being the origin and the sides of the squares in alignment with the x and y axes, the larger circle has the equation
( x − 5 ) 2 + ( y − 5 ) 2 = 2 5 ⟹ x 2 − 1 0 x + y 2 − 1 0 y + 2 5 = 0
⟹ x 2 + y 2 = 1 0 x + 1 0 y − 2 5 ,
and the smaller circle has the equation
( x − 2 5 ) 2 + y 2 = 4 2 5 ⟹ x 2 + y 2 = 5 x .
Thus 5 x = 1 0 x + 1 0 y − 2 5 ⟹ x + 2 y = 5 ⟹ x − 5 = − 2 y .
Plugging this result back into the equation for the larger circle gives us that
4 y 2 + y 2 − 1 0 y + 2 5 = 2 5 ⟹ 5 y 2 = 1 0 y ⟹ y = 2 ,
where we can discard the solution y = 0 . This gives us P ( 1 , 2 ) .
Looking now at the small square, the area B of the lower white region and the area A of the shaded region on the left add to 2 5 − 4 2 5 π , and the area C of the shaded region on the right along with area B add to 8 2 5 π . Thus the total area of the shaded regions will be 2 5 − 8 2 5 π − 2 B . So we must now find B .
Define the points O ( 0 , 0 ) , Q ( 5 , 5 ) , R ( 5 , 2 ) , S ( 5 , 0 ) , T ( 2 5 , 0 ) , U ( 1 , 0 ) . Now ∠ P Q R = ∠ P Q S = tan − 1 ( 3 4 ) , so the area of sector P Q S is 2 2 5 tan − 1 ( 3 4 ) . The area of the region bounded by chord P S and arc P S is then the area of sector P Q S minus the areas of right triangles Δ P Q R and Δ P R S , which comes out to a = 2 2 5 tan − 1 ( 3 4 ) − 1 0 .
The portion of the area B that lies to the right of x = 1 is then the area of Δ P S U minus a , i.e., 4 − ( 2 2 5 tan − 1 ( 3 4 ) − 1 0 ) = 1 4 − 2 2 5 tan − 1 ( 3 4 ) .
The portion of area B that lies to the left of x = 1 is the area of sector P T O minus the area of Δ P T U . Now ∠ P T O = ∠ P T U = tan − 1 ( 2 3 2 ) = tan − 1 ( 3 4 ) . Thus the area of sector P T O is 8 2 5 π tan − 1 ( 3 4 ) , and so the area of the portion of B to the left of x = 1 is 8 2 5 π tan − 1 ( 3 4 ) − ( 2 1 ) ( 2 3 ) ( 2 ) = 8 2 5 π tan − 1 ( 3 4 ) − 2 3 . Thus the area of B is
1 4 − 2 2 5 tan − 1 ( 3 4 ) + 8 2 5 π tan − 1 ( 3 4 ) − 2 3 = 2 2 5 − 8 7 5 tan − 1 ( 3 4 ) .
The area of two shaded regions is then
2 5 − 8 2 5 π − 2 ∗ ( 2 2 5 + 8 7 5 tan − 1 ( 3 4 ) ) = 4 7 5 tan − 1 ( 3 4 ) − 8 2 5 π = 7 . 5 6 9
to 3 decimal places.