Swing out

Classical Mechanics Level 3

In a version of recreational "tubing" people ride on an inflated rubber or soft plastic device (the "tube") that is connected to a motorboat. See this link for a photo and this Wikidedia article .

The length of the rope connecting the tube to the boat is $l$ . The boat moves on a circle of radius $r$ , with velocity $v$ . The tube is swinging out behind the boat and follows it on a circle that is concentric with the circle the boat is making. The force on the tube due to the water, $F$ , is opposite to the tube's velocity, and the magnitude of the force can be expressed as the fraction of the weight $mg$ of the tube (and the people on it) as $F=\mu m g$ .

Determine velocity of the tube in $m/s$ for $l=6.0m$ , $r=6.0m$ , $v=5.0m/s$ and $\mu=0.20$ . For the gravitational acceleration use $g=10m/s^2$ .

The answer is 9.71.

1 solution

Laszlo Mihaly
Nov 25, 2017

My original solution was incorrect. See the correct solution by Steve Chase below. Thanks for the correction.

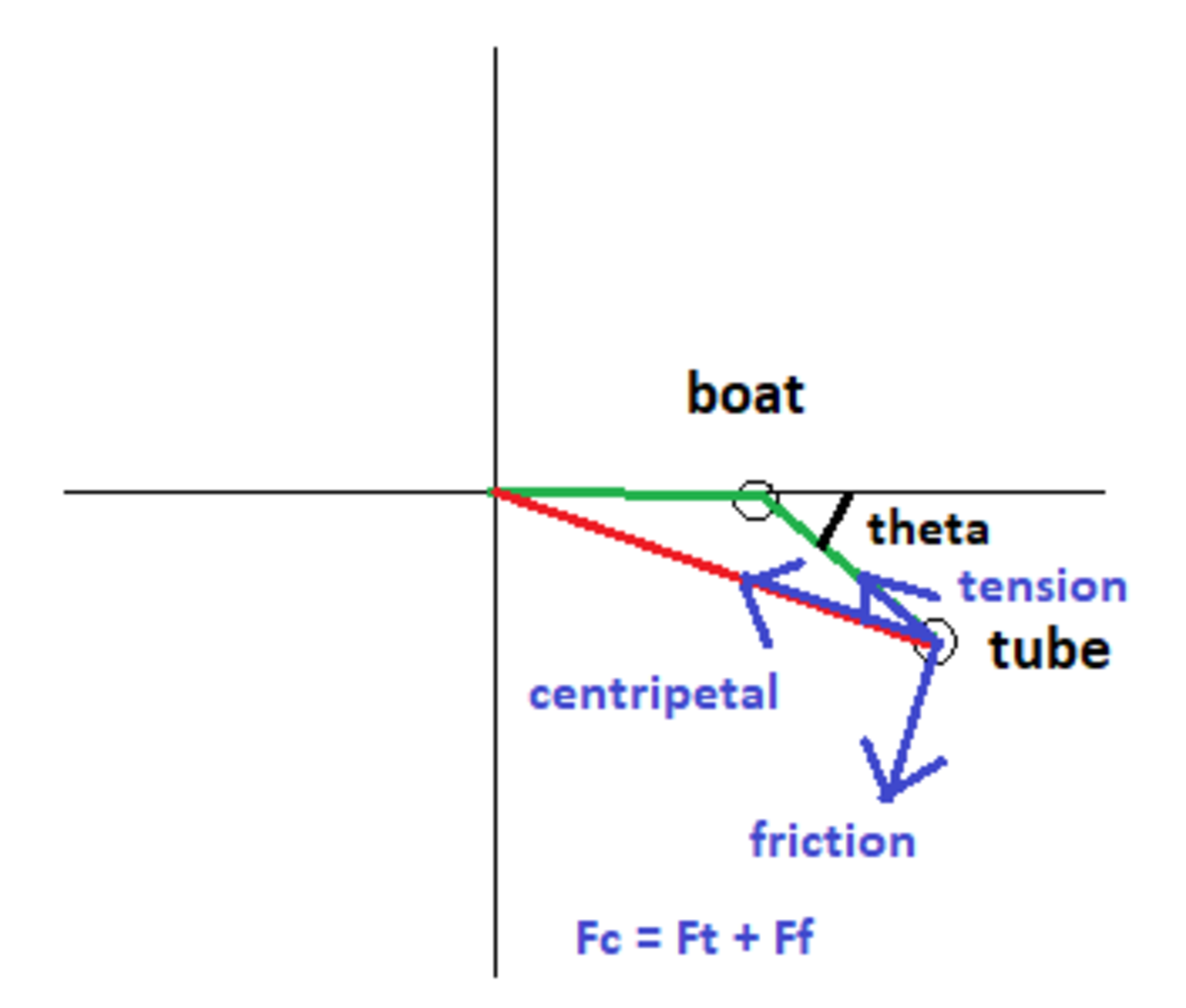
Greetings. This is an interesting problem. I'd like to discuss this one a bit, and see where our paths diverge. Here's the picture I've been working with. There is some angle between the boat-origin line and the rope (theta). Here was my reasoning process:

Sweep over possible $\theta$ values and find the one that checks out based on the process below:

1) The angle $\theta$ determines the circle radius for the tube
2) We know the angular speed from the boat, and we know that the two angular speeds (boat and tube) must be the same
3) Knowing the angular speed and the radius for the tube, we can determine the tangential speed for the tube
4) Then we can calculate the centripetal force for the tube (magnitude and direction, since we know where the tube is)
5) The centripetal force is the sum of two forces: rope tension and friction
6) We know the magnitude and direction of the friction force (assuming we're evaluating a candidate $\theta$ )
7) Calculate the tension force from the centripetal force and from the friction force
8) Check condition: The calculated tension force must be along the line from the tube to the boat.

Based on this, I ended up with $\theta = 27.77^\circ$ and a tube speed of $9.7077 m/s$ . It seems the biggest divergence between our two approaches is that I didn't arrive at an equilateral triangle geometry.

Steven Chase - 3 years, 6 months ago

Steve, I just could not stop thinking about this and I wrote a more detailed solution, still getting the same result. I provided a graph and intermediate results, and also tested the low and high velocity limits. Perhaps if you could look at it and try to find the divergence between the solutions.

Laszlo Mihaly - 3 years, 6 months ago

I find your picture to be more useful than mine. However, I still get the same answer apparently (albeit with a simpler process). Here it is:

Main equations:

$T \, sin \alpha = \mu m g \\ T \, cos \alpha = \frac{m V_t^2}{R}$

Work out expressions for some of the component quantities:

$R = 2r \, cos \alpha \\ V_t = R \omega = \frac{R v}{r} = 2v \, cos \alpha$

Looking again at the second main equation:

$T \, cos \alpha = \frac{4m v^2 cos^2 \alpha}{2r \, cos \alpha} = \frac{2 m v^2}{r} cos \alpha \\ T = \frac{2 m v^2}{r}$

Looking again at the first main equation:

$\frac{2 m v^2}{r} \, sin \alpha = \mu m g \\ sin \alpha = \frac{\mu g r}{2 v^2} \\ \alpha = 13.8865^\circ$

This results in the angle I call "theta" being equal to 27.77.

Steven Chase - 3 years, 6 months ago

@Steven Chase – You are right. I used the wrong speed in the centripetal force (the speed of the boat instead of the speed of the tube.

Laszlo Mihaly - 3 years, 6 months ago

@Laszlo Mihaly – Thanks for engaging with me on this one. It was a neat problem. Shall we have the staff change the answer to 9.7077?

Steven Chase - 3 years, 6 months ago

@Steven Chase – I sent in a report and asked them a few hours ago. --Laszlo

Laszlo Mihaly - 3 years, 6 months ago

Could you please also report it? Apparently one report does not trigger a fast response.

Laszlo Mihaly - 3 years, 6 months ago

Swing out

The answer is 9.71.

1 solution

0 pending reports