Symmetry for the win! <3

This question (and its predecessor) is much harder than the author thinks, since there is a significant problem in defining what is actually meant by a " $2$ -dimensional completely random walk". Doing this properly requires some significant theory from stochastic differential equations.

What is actually meant by a " $2$ -dimensional completely random walk" is what is called a $2$ -dimensional Wiener process, which means that the coordinates of the moving particle, relative to its starting point, are $(X_t,Y_t)$ where $X_t$ and $Y_t$ are independent identically distributed Brownian motion processes. In particular this means that both $X_t$ and $Y_t$ have the Normal distributions $N(0,2Dt)$ , where $D$ is the diffusion coefficient of the system. Further analysis shows that the probability distribution function of the first hitting time $T$ for $Y_t=1$ is $f_T(t) \; =\; \frac{1}{\sqrt{4\pi D t^3}} \mathrm{exp}\left(-\frac{1}{4Dt}\right)$ The probability that $X_t < 1 + \sqrt{2}$ is $\int_{-\infty}^{1+\sqrt{2}} \frac{1}{\sqrt{4\pi Dt}} \mathrm{exp}\left(-\frac{x^2}{4Dt}\right)\,dx \; = \; \frac12\left(1 + \mathrm{erf}\left(\frac{1 + \sqrt{2}}{\sqrt{4Dt}}\right)\right)$ Thus the probability that the random Wiener process crosses the $x$ -axis in the positive half is $\begin{aligned} \int_0^\infty \frac12\left(1 + \mathrm{erf}\left(\frac{1 + \sqrt{2}}{\sqrt{4Dt}}\right)\right) f_T(t)\,dt & = \; \int_0^\infty \frac12\left(1 + \mathrm{erf}\left(\frac{1+\sqrt{2}}{\sqrt{4t}}\right)\right) \, \frac{1}{\sqrt{4\pi t^3}}\mathrm{exp}\left(-\frac{1}{4t}\right)\,dt \\ & = \; \frac{1}{2\sqrt{\pi}}\int_0^\infty \left(1 + \mathrm{erf}\left(\frac{1+\sqrt{2}}{2}u\right)\right)\,\mathrm{exp}\left(-\frac14u^2\right)\,du \; = \; \tfrac78 \end{aligned}$ making the desired answer $\boxed{\tfrac18}$ .

Proceeding the explanation, view the following diagram, 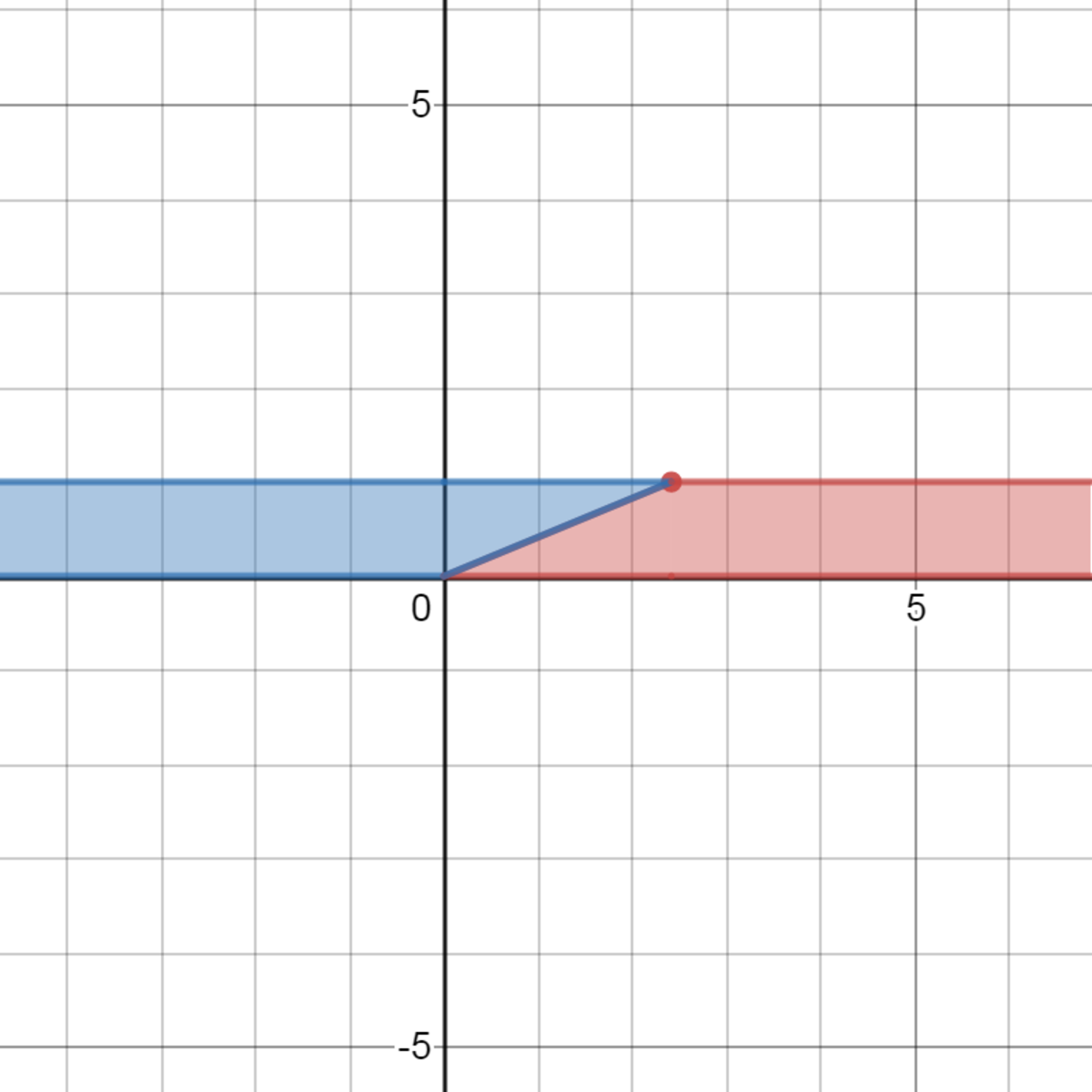I apologize for the image's vary large and unnecessary size.

As stated, a person is heading in a random direction from a specific starting point (marked as a red point where both regions touch) to which they are to reach the x -axis. I have purposely divided these two regions so that one can tell whether the person will hit the negative or positive part of the x -axis based off whether their first step is in the red or blue zone. If one takes their first step in to the red they will meet the positive x -axis, while the opposite is true for the blue zone. The individual must head in one of these two zones or they will never reach the x -axis. Now, we must determine the probably of reaching the negative part of the x -axis. To determine the probability of reaching the specified zone, we will make a ratio comparing the portion of directions that will reach the zone compared to the portion of directions that will just hit the x -axis. To hit the x -axis in general, the person just has to walk in within a $\pi$ radian sector (or 180 degree sector). The 180 degree sector (which is both read and blue) holds the portion of directions that will just the x -axis in general. Normally, being that starting point is just above the center on the y -axis, the probability would be $\frac{1}{2}$ (or there is a 90 degree region for each zone) but the blue region, relative to the starting point, is angularity skewed. The angle of the region that reaches the negative x -axis is equivalent to 90 degrees (or $\frac{π}{2}$ ) minus the angle of the right triangle, where each leg is equivalent to 1 and $1+\sqrt{2}$ , and the hypotenuse (which doesn't matter in this case) is the distance from the starting point to the center. The angle between the two legs on this triangle is equivalent to $arctan(\frac{1+\sqrt{2}}{1})$ , which, based off the given hint, is the angle $\frac{3π}{8}$ . To calculate the angle of the region, we must subtract $\frac{π}{2}$ ) by $\frac{3π}{8}$ . Now, the following is a ratio between these parts:

$\frac{\frac{π}{2}-\frac{3π}{8}}{π}=\frac{1}{8}$

So I assumed each walk to be a straight line from the given point. This line will always have that given coordinate, so what's variable is the gradient. If this line intercepts the x-axis (positive or negative) then it makes an angle, which is also variable and can be found with trigonometry. For instance, if the line intercepts the origin then the angle the line makes with the horizontal is arctan $\frac{1}{1+\sqrt{2}}$ or $\frac{pi}{8}$ . This angle goes from 0 to pi radians. Any line that makes an angle to the horizontal greater than $\frac{pi}{8}$ crosses the positive x-axis, and an angle less than this produces a line that crosses the negative x-axis. If the angle the line makes is random, we need to find the probability that a random angle from 0 to pi radians is less than $\frac{pi}{8}$ . Dividing $\frac{pi}{8}$ by pi gives $\frac{1}{8}$