T-Junction Oscillation
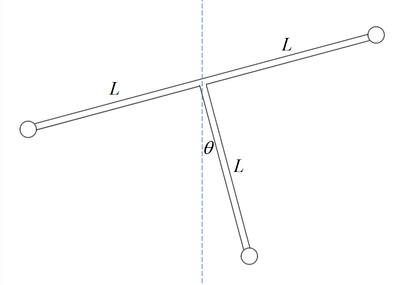
Three light rods, each with a length of L , are rigidly connected to form a T-shape frame. Three identical particle-like balls are fixed at the free ends of the rods. The frame is pivoted at the T-junction and can rotate without friction vertically.
If the angular frequency of oscillation of the frame is given by
ω 2 = α L g
find α .
Bonus: Show how we can compute the time period when the initial angle θ is no longer small.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase @Karan Chatrath Can we solve using Newton laws.?
Log in to reply
Yes, using the rotational form of the 2nd Law. τ = I θ ¨
Log in to reply
@Steven Chase can you post that solution, my SHM is bit weak.
Log in to reply
@Talulah Riley – m g L cos θ − m g L cos θ − m g L sin θ = 3 m L 2 θ ¨ − m g L sin θ = 3 m L 2 θ ¨ − g sin θ = 3 L θ ¨
Log in to reply
@Steven Chase – @Steven Chase Thank you so much. Have a look on new problem and check last 3 hour notifications whenever you will be free. :) :)
@Steven Chase Thanks for the solution. Upvoted.
For small initial angle θ of a compound pendulum , we can find the period of the pendulum by first finding the equivalent length of pendulum given by:
L e q = m R I
where I and m are the moment of inertia and m of the pendulum respectively, and R is the distance between the pivot point and the center of mass. Then the angular frequency is given by:
ω 2 = L e q g
For this problem, let the mass of each of the three balls be m . Then the moment of initial of the pendulum is I = 3 m L 2 .
Using the pivot point be the origin and the coordinates of center of mass be C ( x c , y c ) , where y increases vertically down. Then x c = 3 m m L − m L + 0 = 0 and y c = 3 m 0 + 0 + m L = 3 L . Therefore R = 3 L .
Then L e q = 3 m ⋅ 3 L 3 m L 2 = 3 L and ω 2 = 3 L g ⟹ α = 3 .
Efficient approach. Thanks for the solution
Log in to reply
Glad that you like it. I think members should learn this approach for simple problem. You should mention what L is in your problem. Anyway, I will edit it for you with a few picture. I am a moderator.
Log in to reply
Oh, nice catch. I indeed did not specify the length. Thanks again for your feedback. I'm realising that my problem statements have scope for refinement.
Thanks for the edits to the statement.
The combined gravitational potential energy of the two side masses is constant. It can therefore be neglected.
Kinetic energy, potential energy, and Lagrangian:
T = 2 3 m L 2 θ ˙ 2 V = − m g L cos θ L = T − V = 2 3 m L 2 θ ˙ 2 + m g L cos θ
Equation of motion:
d t d ∂ θ ˙ ∂ L = ∂ θ ∂ L
This results in:
3 m L 2 θ ¨ = − m g L sin θ 3 L θ ¨ = − g sin θ
For small angles:
3 L θ ¨ = − g θ θ ¨ = − 3 L g θ
This corresponds to simple harmonic motion with the following angular frequency:
ω 2 = 3 L g
To compute the time period for large oscillations, probably the easiest thing to do is just run a numerical simulation using the following equation for the double-dot term.
3 L θ ¨ = − g sin θ
Another way is to use conservation of energy:
∣ V ( θ ) − V ( θ 0 ) ∣ = 2 3 m L 2 θ ˙ 2 = 2 3 m L 2 ( d t d θ ) 2
Re-arrange to obtain an expression for d t in terms of θ and d θ , and integrate this expression to derive the time period.