Tangent at a point
Given a circle (without the center) and a point P on the circle, how many moves does it take to draw a tangent to the circle at that point?
All terminology in this question is explained in the first note of my straightedge and compass set. More straightedge and compass constructions can be found there.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The answer to this question is incorrect. There is 3 moves required to do so.
-
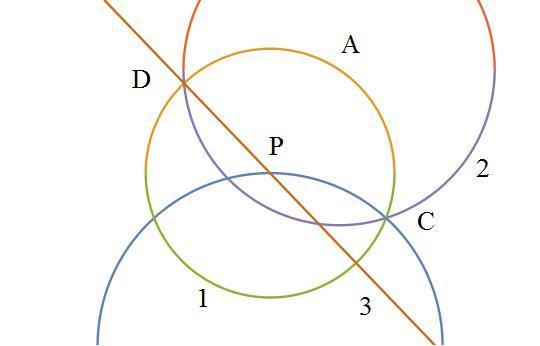
Pick an arbitrary point A on the circle, close to P . (0 moves)
-
Draw a circle centred at A passing through P and intersecting the circle again at C . (1 move)
-
Draw a circle centred at P passing through C . Let it intersect the circle centred at A at D . (2 moves)
-
Draw P D . (3 moves)
P D is the tangent to the circle.
Note: If you would like to confirm your answer with somebody else, I would be happy to lend you a hand. I got 49/50 gold medals on Euclid the Game which requires these sorts of constructions.
Log in to reply
B D is the tangent of the circle passing through point A that is on the circle. How is that such a tangent can always be found, regardless of where point B is picked? Most of time, for arbitrary B , there cannot be a tangent passing through both A and B . Can you clarify?
You start start with a given point P that is on the circle. Then find a way to draw a line through P that is tangent to the circle.
Log in to reply
OK, the problem was slightly edited, but my construction still holds. I have edited it, and you can check to see if it works.
Log in to reply
@Sharky Kesa – It still doesn't make any sense to me. Here's what I have, using your new instructions.
Don't you have a way to paste here your work on Euclid the Game?
Log in to reply
@Michael Mendrin – Sorry, I typoed the instructions. I have fixed it.
Log in to reply
@Sharky Kesa – Now finally that does make sense, as point A is restricted to the circle itself. Then it's feasible to construct another point D dependent on where A is such that PD is tangent to the circle. Very nice!
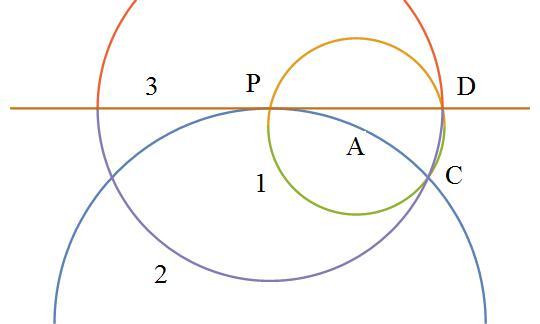
Log in to reply
@Michael Mendrin – Yup :). It isn't very hard to prove this is a tangent either. An easy extension problem is to draw the other tangent in 2 more moves.
Sharky, please show a figure of how this is done, because it is not making any sense to me. This is what I have
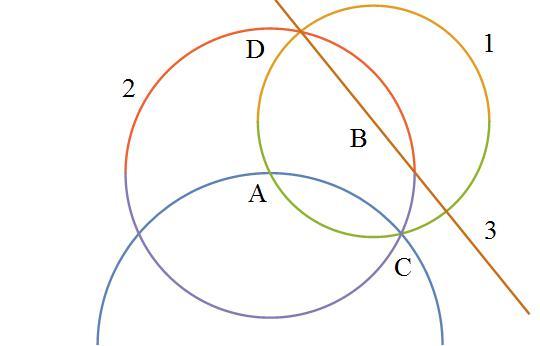
Can you please tell me the definition of a "move " ??
Okay sorry about that-
I haven't really had much time to think about these questions. @Calvin Lin please fix this.
I'll see if I can come up with a more original problem and next time I'll probably put a lot more thought into it.
Log in to reply
Thanks. I have updated the answer to 3.
Log in to reply
My answer is still written as incorrect, as I chose the closest number to 3, which was 5.
Log in to reply
@Sharky Kesa – K, given that this was MCQ, those who answered 5 have now been marked correct.
This can be done in 6 moves, which, apparently, is not one of the choices.
1) Draw circle of arbitrary radius centered at P, intersecting circle at A, B
2) Draw line through A, B and extend beyond
3) Draw circle of radius AB centered at B, intersecting line AB at C
4) Draw circle of radius PB centered at B
5) Draw circle of radius PB centered at C, intersecting other circle at D
6) Draw line PD, which is the tangent to the circle
Log in to reply
We've already got a better solution below (see my comment). 3 moves are sufficient so is the correct answer.
Log in to reply
Read my comment to your comment. It does read like what you are doing is constructing "any" tangent to the circle, not the one passing through a given point P.
Again if you find a solution that requires less than 3 I'll be happy to change it.